预测模型---001-灰度预测

灰度预测

使用条件: 样本点数较少 仅6-15个左右
呈现指数或者曲线关系

灰度预测简介

通过少量 不完全的信息 建立数据模型并且进行预测的一种方法
灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论

灰色预测是对灰色系统 所做的预测.
特别是它对时间序列短、统计数据少、信息不完全系统的分析与建模，具有独特的功效，因此得到了广泛的应用.

灰色系统是黑箱概念的一种推广。我们把既含
有已知信息又含有未知信息的系统称为灰色系统

灰色系统的特点
（1）用灰色数学处理不确定量，使之量化.
（2）充分利用已知信息寻求系统的运动规律.
（3）灰色系统理论能处理贫信息系统.

灰色生成

将原始数据进行数据处理 就叫做生成 目的: 突出数据的内在规律

常用的灰色系统的生成方式有:
	累加生成
	累减生成
	均值生成
	级比生成

GM(1.1)模型

推到公式 网上有很多 本处只给出结果

k 时间序列
 求解 a u

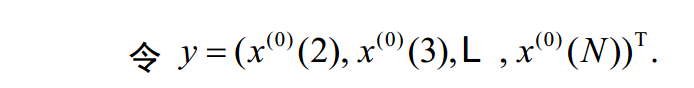
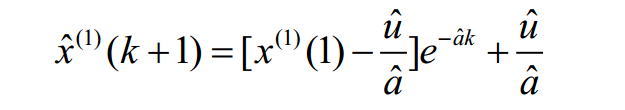
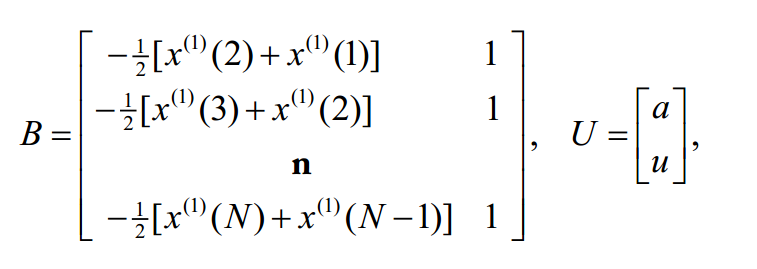
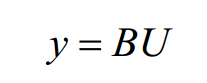
可以解出 a u

模型使用方法

1. 灰度生成
2. 计算a u 生成模型

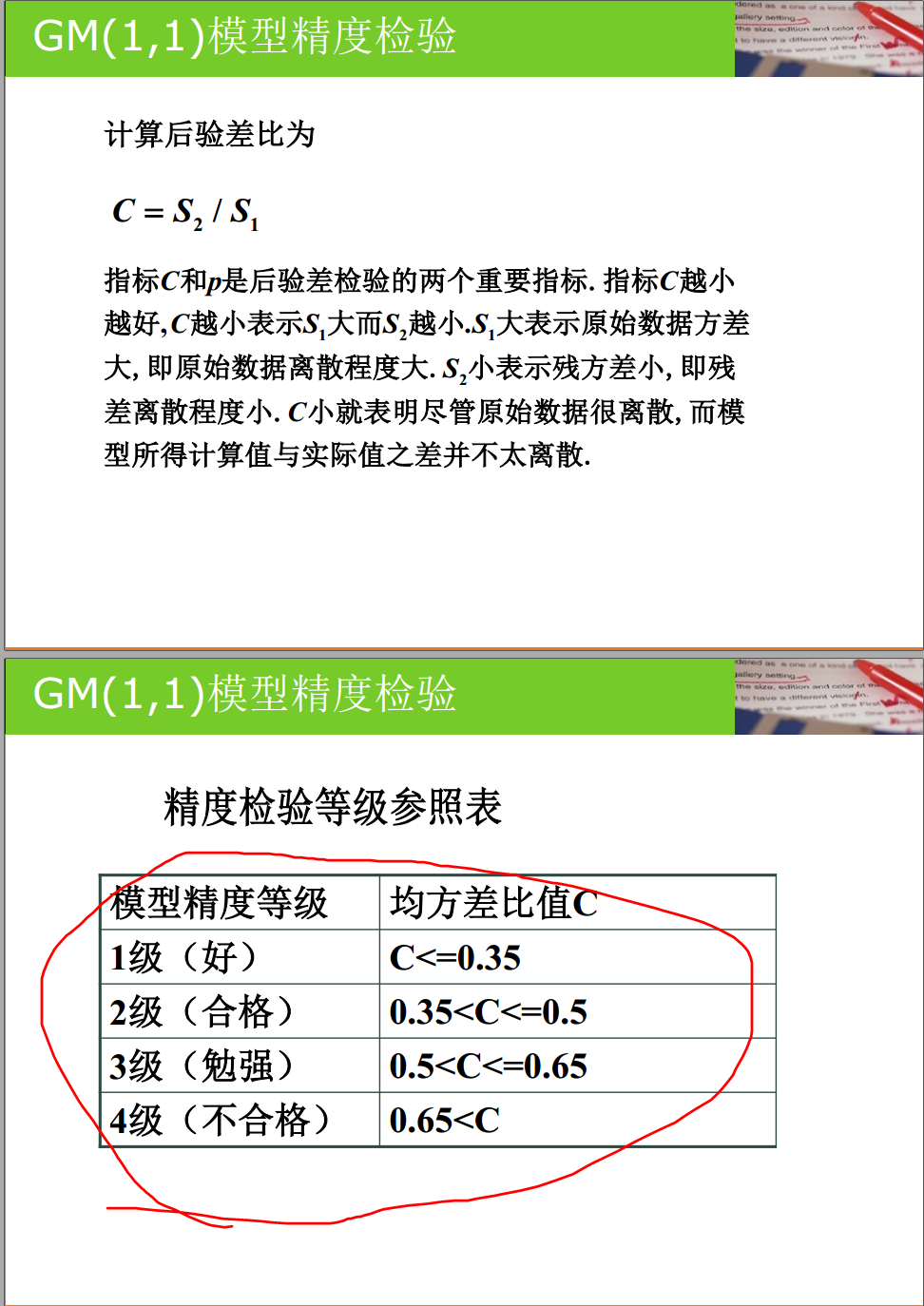
精度判断

实现

点击查看代码

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一（替换sans-serif字体）
plt.rcParams['axes.unicode_minus'] = False # 步骤二（解决坐标轴负数的负号显示问题）
# 原始数据X
X=[21.2, 22.7, 24.36, 26.22, 28.18, 30.16, 32.34, 34.72, 37.3, 40.34,44.08, 47.92, 51.96, 56.02, 60.14, 64.58, 68.92, 73.36, 78.98, 86.6]

# 训练集
X0 = np.array([21.2, 22.7, 24.36, 26.22, 28.18, 30.16, 32.34, 34.72, 37.3, 40.34])
# 测试集
X_test =[44.08, 47.92, 51.96, 56.02, 60.14, 64.58, 68.92, 73.36, 78.98, 86.6]
# 分布特征检验
## 计算级比
lens = len(X0)
lambds = [X0[i-1]/X0[i] for i in range(1, lens)]
## 计算区间
X_min = np.e**(-2/(lens+1))
X_max = np.e**(2/(lens+1))
## 检验
is_ok = True
for lambd in lambds:
    if (lambd < X_min or lambd > X_max):
        is_ok = False
    if (is_ok == False):
        print('该数据未通过检验')
    else:
        print('该数据通过检验')

# 一阶累加XR1
X1=X0.cumsum()
print("一阶累加序列X1:",X1)
# 预测模型背景值
L = (np.array([-0.5*(X1[k-1]+X1[k]) for k in range(1,len(X1))])).reshape(len(X1)-1,1)
# 数据矩阵Y_n、B
Y_n = (X0[1:]).reshape(len(L),1)
B =np.hstack((L,np.ones(len(L)).reshape(len(L),1)))
# 求灰参数
a,u = np.linalg.inv(np.matmul(B.T, B)).dot(B.T).dot(Y_n)
print("灰参数a：",a,"，灰参数u：",u)
# 构建XR1的微分方程，并求解XR1,XR1为预测序列
def get_predict(init,u,a,k):
    pred = (init-u/a)*np.exp(-a*(k-1))+u/a
    return pred[0]
X1_hat = [get_predict(X0[0],u,a,k) for k in range(1,len(X1)+1)]
print(X1_hat)
X0_hat = np.diff(X1_hat)
X0_hat = np.hstack((X1_hat[0],X0_hat))
print(X0_hat)
plt.grid()
plt.plot(np.arange(len(X0)), X0, '->')
plt.plot(np.arange(len(X0)), X0_hat, '-o')
plt.legend(['负荷实际值','灰色预测模型预测值'])
plt.show()
# 评估指标
S1 = np.var(X0_hat) # 预测结果方差
S2 = np.var(X0-X0_hat)# 残差方差
C = S2/S1 # 后验差
## 结果
if (C <= 0.35):
    print('1级，效果好')
elif (C <= 0.5 and C >= 0.35):
    print('2级，效果合格')
elif (C <= 0.65 and C >= 0.5):
    print('3级，效果勉强')
else:
    print('4级，效果不合格')
# 测试集
X1_test_hat = [get_predict(X0[0],u,a,k) for k in range(1,len(X0)+len(X_test)+1)]
X0_test_hat = np.diff(X1_test_hat)
X0_test_hat = np.hstack((X1_test_hat[0],X0_test_hat))
plt.grid()
plt.plot(np.arange(len(X_test)), X_test, '->')
plt.plot(np.arange(len(X_test)), X0_test_hat[len(X0):], '-o')
plt.legend(['负荷实际值','灰色预测模型预测值'])
plt.title('测试集')
plt.show()