对抗攻击方法一览
背景
神经网络在过去的几年和几十年已经获得了长足的进步,神经网络的应用已经遍布我们生活的各个角落。但是与此同时,也有人发现神经网络并不像我们预期的那么具有鲁棒性,仅仅在图片中添加一个微笑的扰动就可以改变神经网络最后的预测结果,这些技术被称为对抗攻击。对抗攻击是指在干净的图片中添加微小的扰动,使神经网络(DNN)产生误判,但人的肉眼却无法察觉的一项技术,最早是在Szegedy等人在《Intriguing properties of neural networks》中提出。
在这篇论文发表后,就激起了大家对对抗攻击研究的热情,于是就不断的有新的对抗攻击方法被提出,力求将网络攻击后的准确率攻击的越低越好,但与此同时,又不断的有人提出了如何改进模型结构或者新的训练方法,来提升模型面对各种对抗攻击方法时的鲁棒性,随着大家的不断深入的研究,这也变成了一个功与防,矛与盾的问题。接下来,我也将对我了解到了攻击或者防御方法做一个大概的梳理。本文的内容很大程度上参考了这篇综述:Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey
分类
如果对对抗攻击方法按照是否知道被攻击网络的结构或者参数来分类,那么可以分为白盒攻击和黑盒攻击。在一般来说,如果攻击的时候有利用到被攻击网络的梯度信息,那么这个攻击方法就是一种白盒的攻击方法,因为白盒攻击知道了被攻击网络模型的具体结构和参数,所以攻击的强度也会很大,与此对应的就是黑盒攻击,对于黑盒攻击来说,攻击者获取不到模型的各种细节,只知道模型输入和输出,整个模型对他来说就是一个黑漆漆的盒子,这也是黑盒这个名字的来源。虽然白盒攻击的强度会比黑盒攻击高很多,但是在现实情况下,黑盒攻击更具有现实意义,因为攻击者其实很难直接的将你的模型拿来做分析,进行白盒攻击。
如果将对抗攻击方法按照攻击采取的形式,那么可以将网络的攻击分为目标攻击和非目标攻击。这两种攻击的主要区别就是对模型的攻击方向是不是确定的,例如说,有一张猫🐱的图片,你想让攻击之后的图片被网络识别为狗🐕,那么,这就是一种典型的目标攻击,与此对应的,如果你只是想让网络不正确识别到猫🐱,可能攻击之后识别为蛇🐍,车🚗或者其他的,这种就是典型的非目标攻击。
如果按照攻击的方法来划分的话,可以将网络分为单步攻击、迭代攻击和基于优化的攻击。区分这三者就比较的容易,单步攻击就是在攻击中只攻击一次,这种攻击方法的优点就是攻击的速度非常的快,但是缺点也比较的明显,就是攻击的强度很小,单步攻击的代表就是FGSM;多步攻击就是单步攻击的改进版本,不像单步攻击那样简单的移动一步,而是按照一定的步长,多次的攻击,代表就是PGD;基于优化的攻击将寻找合适的对抗样本看作为一个优化问题,根据设置的优化目标去不断的优化扰动,其代表就是CW。
常用术语
\(L_0\)范数,\(L_2\)范数,\(L_\infty\)范数
对于各种的攻击算法中,这几个范数出现的频率特别高,这三个范数的存在主要是为了去更统一的规范各个攻击算法产生的扰动的范围。
-
\(L_0\)范数:扰动的像素点数量
-
\(L_2\)范数:原始图像和扰动之后的图像之间,所有像素点距离绝对值的总和
-
\(L_\infty\)范数:在所有的扰动中,绕动最大的那一个
所以其实可以看到,\(L_0\)范数约束的是对抗样本被扰动过的像素点数量,被扰动的越少,那\(L_0\)范数就越小,\(L_2\)范数是对扰动整体进行了一个约束,要求扰动整体的绝对值之和要小于某个值,对于\(L_\infty\)范数来说,它只限制了扰动的最大值,只要扰动不超过这个规定的值,就是合理的。
攻击方法
Box-constrained L-BFGS
论文地址:Intriguing properties of neural networks
Szegedy等人在发现网络可以被微小的扰动干扰之后,就提出了产生对抗样本的方法,其提出的方法大致为:
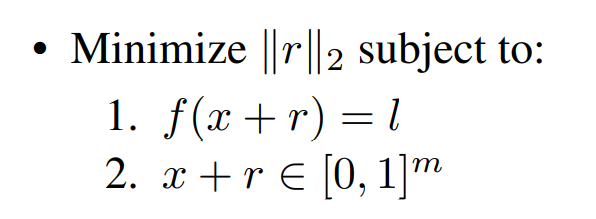
其中r为生成的扰动,f为分类器,l为目标类别,所以改攻击方法就是在尽可能将扰动降低的过程中,让网络误判对抗样本为目标类别,同时还需要保证添加上扰动的对抗样本还在0到1的范围内。但是作者发现这个优化的问题会过于的复杂,所以将优化的问题进行了一定的简化,变成了:
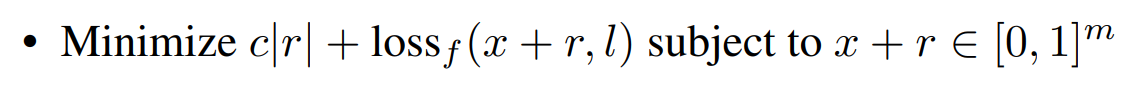
相较上面的公式,这里的优化问题多了一个惩罚因子c,用来权衡两者的关系,其他与上式基本一样,但是到这里,整个优化问题就变为了一个凸优化的问题。
FGSM
论文地址:Explaining and Harnessing Adversarial Examples
FGSM是GoodFellow(大牛)提出的一种攻击方法,其攻击的手段也十分的直观,因为我们在训练网络的过程中,都是想让网络的参数朝着梯度下降的方向去调整,那么,我们就可以在图像上添加扰动,这个扰动可以朝着梯度上升的方向去生成,这样子就可以让网络预测出来的损失尽可能的大,预测的结果也就会偏离。FGSM的扰动生成公式:

可以看到对抗样本加上了朝着梯度上升生成的扰动,那这个对抗样本就会离真实样本越来越远,达到了对抗样本的目的。与此同时,也会有目标攻击的FGSM,其公式与原始的FGSM十分相似:
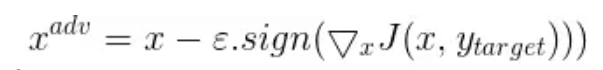
可以观察到,与原始的FGSM的主要区别就是将加号变为了减号,同时把与真实标签做Loss变为了与目标标签做Loss,这样子就会让图片朝着目标标签演变。
Basic Iterative Methods(BIM)
论文地址:Adversarial examples in the physical world
相较于FGSM的一下子走一大步,Basic Iterative Methods(BIM)将大的步长分解为许多小的步长,然后扩展为多步去逐步的增大模型的Loss,其运算的流程如下:
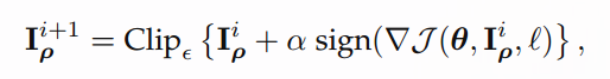
第i+1次的迭代结果基于第i次的结果,同样也是基于梯度,然后不断的去增大模型的Loss。同样的,BIM也有目标攻击的版本,其变种同上面的FGSM的变种一样,将真实标签变为了目标标签,同时将加上梯度变为减去梯度。
这里可能会发现上面的实现过程与我们熟悉的PGD十分的相似,甚至有点看着一模一样,事实也的确如此,PGD作为BIM的变体,相较于BIM的改进是在进行攻击的时候,会以随机的初始噪声来初始化自己的扰动,这个改进也证明了自己的有效性,PGD是现阶段十分强力的攻击方法
Jacobian-based Saliency Map Attack(JSMA)
论文地址:The Limitations of Deep Learning in Adversarial Settings
相较于前面的几种对抗攻击方法使用的是L2范数或者无穷范数去限制对抗样本,JSMA的方法将使用L0范数去限制被扰动的像素点个数,但是对每个扰动的像素点的扰动范围没有确切的要求。对于如何选择被扰动的像素点,这里选择的是使用显著图(Saliency Map)这个概念去选择对误判贡献最大的那几个像素点。
在计算的过程中,作者使用了雅可比矩阵去求得向前传播的偏导数,从而获取哪些像素位置对误分类神经网络有最大的贡献,向前导数矩阵的计算公式如下:
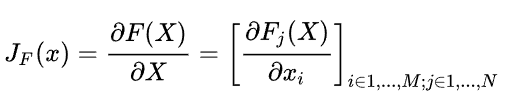
这里可能会疑惑,向前传播的求导与我们平时使用向后传播的求导有何不同?首先,我们平时在使用向后传播的时候,求导是在代价函数,也就是我们求的Loss函数与输入变量之间求导,这些过程都被封装在backward这个方法中,这里的向前传播是神经网络的最后一层函数F与输入变量之间的求导
在求完雅可比矩阵之后,我们就可以分析出哪些才是我们需要去扰动的像素点,文中使用了一下的计算方式:
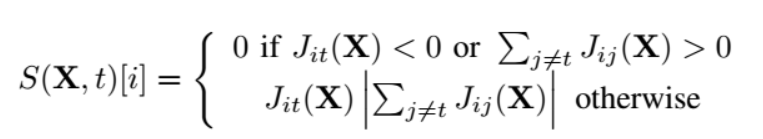
这个公式中,i表示的是输入特征的第i个特征,X是输入的变量,t为目标类别。那么这个公式的上半部分就表示的是拒绝对判断为目标标签t有副作用的像素,或者让对抗样本会判断为非目标标签t有正作用的像素也置为0,然后下半部分是将对对抗样本判断为目标标签t有积极作用的像素增大权重。从上面的描述就可以看出,JSMA是一种典型的目标攻击,需要指定目标标签t。
One Pixel Attack
论文地址:One Pixel Attack for Fooling Deep Neural Networks
这是一种比较极端的攻击方法,同上面的JSMA攻击方法一样,它也是L0范数下的攻击。就像这个算法的名字一样,它只改变了原图中的一个像素,就能使模型对攻击后的图片产生误判。在最初看到这个攻击算法的时候,比较直观的想法就是遍历图片的每个像素,然后逐一的去尝试,但是这样子会十分的耗时,就拿CIFAR10数据集来说,一张图片就要便利32*32*3次,这代价太大,于是作者的解决办法是使用了差分进化算法,会让寻找最优的像素的时间变少。

Carlini and Wagner Attacks(C&W)
论文地址:Towards Evaluating the Robustness of Neural Networks
CW算法是一种基于优化的算法,其优化的目标就是产生一种人肉眼看上去十分干净,但是会让机器产生误判的对抗样本。至于为什么要叫这个名字,与其本身的攻击方法没有任何关系,这个是论文两个作者的名字拼起来的来的。
对于CW来说,需要确定一个优化的目标,在文中,作者将这个优化的目标设置为了:
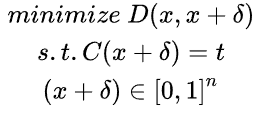
这个优化的目标就是在能让模型误判的前提下,尽可能的让扰动小。在这个优化的过程中,有一个很有意思的技巧,就是作者需要确定生成的对抗样本是一个正常的图片,即范围应该在0到1之间,但是如果直接使用torch.clamp函数的话,就会让被裁切掉的部分失去梯度,然后在之后的优化过程中不再发生变化,这是我们不想看到的,所以作者先是将一张正常的图片映射到了(-inf, +inf)的范围,使用的是atanh函数,然后在这个范围进行优化,优化完之后经过一个Tanh函数,就恢复了原来图片的范围,这样就可以比较方便的优化出一个对抗样本。CW的攻击性很强,而且相较于FGSM和PGD,它的扰动对人的肉眼来说几乎不可见,但是其有一个很大的缺点,就是非常非常非常的慢。
DeepFool
论文地址:DeepFool: a simple and accurate method to fool deep neural networks
DeepFool的目标是寻找到可以让模型产生误判的最小扰动,这就好比在简单的多分类场景中,机器学习是使用一个超平面去区分不同的类别,那使一个类别产生误判最简单的方法就是朝着这个超平面移动,这就是最小的扰动。在本篇论文中,作者将要寻找的最小扰动定义为了:

其中r就是要寻找的最小扰动,K就是分类器。
作者先在二分类中演示了DeepFool,如下图所示,一个超平面将空间分为了两半,超平面的两边代表了模型识别的两类
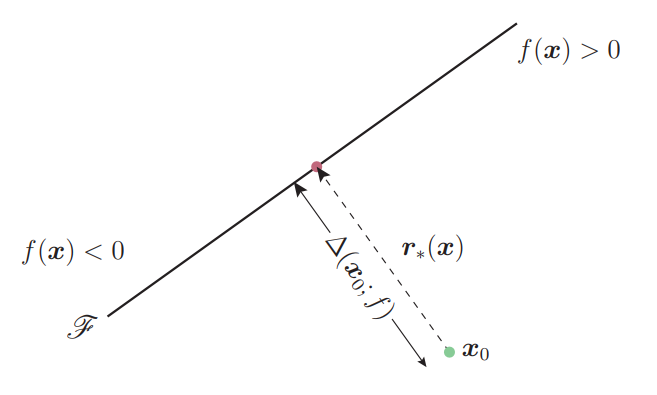
其中超平面的表达式为:

则最小的扰动距离就可以被定义为:
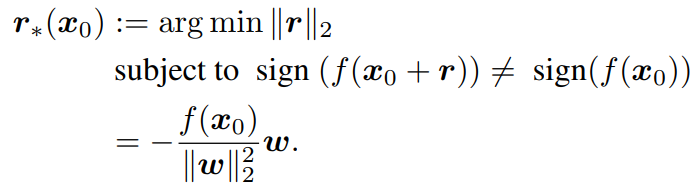
对于通用的分类器来说,寻找这个最小的扰动距离需要一个迭代的过程去寻找,作者在文中给出的伪代码如下:

即不断的朝着超平面的方向前进,直到样本被模型误判。
Adversarial Transformation Networks (ATNs)
论文地址:Adversarial Transformation Networks: Learning to Generate Adversarial Examples
这篇论文不同于之前想要分析模型的种种特点,这里想直接训练一个模型,将原图作为输入,然后输出就为对抗样本,可以说是一种比较巧妙的方法。在这个网络的训练过程中,也会设定一个优化目标去指导模型的训练,这里将优化的目标设定为了:
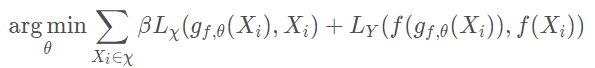
其中\(f()\)为训练好的分类模型,\(g()\)为我们要训练的产生对抗样本的模型,\(L_X\)和\(L_Y\)均为损失函数,在论文中,\(L_X\)为\(L_2\) Loss,\(L_Y\)的定义为:
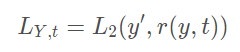
这里的\(r(y, t)\)是作者定义的一个reranking函数,主要的目的就是指引模型误判为指定的类,其定义为:
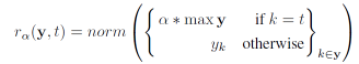
主要的作用就是将目标类别t的值乘上一个倍数,以让模型朝着这个方向去训练,然后不改动其他类别的值,这样的好处是top2的准确率是不会变的,这也会让扰动之后的图片更加的正常。
Universal Adversarial Perturbations
论文地址:Universal Adversarial Perturbations: A Survey
这篇论文提出的是想要生成一个通用的扰动,这个扰动添加到任意一张图上,都可以让网络被误分类到目标类上,着篇论文提出的方法与前面介绍的DeepFool相似,都是将图像推出分类的边界,不过与DeepFool不同的是,这个扰动是在遍历许多张图片后找到的,是针对所有图片的通用扰动。
UPSET and ANGRI
论文地址:UPSET and ANGRI : Breaking High Performance Image Classifiers
与上面的攻击方法不同,这个攻击方法是一种黑盒攻击,其对抗样本的产生是按照以下的公式:

U()就是论文中提出的UPSET网络,R()是一个残差网络,s为一个缩放因子,然后将产生的对抗样本限制在(-1, 1)的范围里。
总结
上文介绍了几种方法都是一些比较出名的攻击方法,有的是目标攻击,有的是非目标攻击,有的是黑盒,有的是白盒,但攻击的手段也肯定远远不止这几种,更何况这篇综述写于18年,这里也只是介绍了我了解过的一些攻击方法。

 神经网络在过去的几年和几十年已经获得了长足的进步,神经网络的应用已经遍布我们生活的各个角落。但是与此同时,也有人发现神经网络并不像我们预期的那么具有鲁棒性,仅仅在图片中添加一个微笑的扰动就可以改变神经网络最后的预测结果,这些技术被称为对抗攻击。
神经网络在过去的几年和几十年已经获得了长足的进步,神经网络的应用已经遍布我们生活的各个角落。但是与此同时,也有人发现神经网络并不像我们预期的那么具有鲁棒性,仅仅在图片中添加一个微笑的扰动就可以改变神经网络最后的预测结果,这些技术被称为对抗攻击。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号