鞅在一类图上随机游走问题中的应用

1 引言

图上随机游走问题是一类比较经典而难解决的概率期望问题，然而，由于随机过程的模型变化多端，因此较难找到突破口。除了朴素高斯消元外没有较为通用且快速的算法，从而无从下手。随机过程中的鞅是研究停时问题的有力工具，是解决这一类问题的重要理论。本文将首先介绍鞅的停时定理，并用其分析一类具有特殊性质的图上随机游走的期望步数问题，最终得到了递推公式。

2 鞅与停时定理

2.1 随机过程

2.1.1 测度空间

测度空间一般用三元组 \((X,\mathcal{A},\mu)\) 表示。其中 \(X\) 是一个非空集合；\(\mathcal{A}\) 是 \(X\) 的子集构成的且且满足对交并补运算封闭的集族；而 \(\mu\) 为 \((X,\mathcal{A})\) 上的一个测度。

若\(\mu : \mathcal{A} \rightarrow \mathbb{R}\) 是可测空间 \((X,\mathcal{A})\) 上的一个测度，则 \(\mu\) 满足：

  • 非负性：对任意 \(E \in \mathcal{A}\)，满足 \(\mu(E)\ge 0\)。
  • 空集测度为零：\(\mu(\varnothing)=0\)。
  • 可数可加性：若 \(\{E_i\}_{i=1}^{\infty}\) 满足 \(\forall i\neq j\)，\(E_i \cup E_j = \varnothing\)，则 \(\mu\left(\bigcup\limits_{i=1}^{\infty}E_i\right)=\sum\limits_{i=1}^{\infty}\mu(E_i)\)。

2.1.2 概率空间

概率空间 \((\Omega,\mathcal{F},P)\) 是一个测度为 \(1\) 的测度空间，即 \(P(\Omega)=1\)。其中 \(\Omega\) 称为样本空间，其中的元素 \(\omega\) 称为样本点或基本事件。\(\mathcal{F}\) 是 \(\Omega\) 上满足对交并补运算封闭的事件集合，其中的元素 \(\Sigma\) 称为事件，满足 \(\Sigma \subset \Omega\)。

\(P\) 是在可测空间 \((\Omega,\mathcal{F})\) 上定义的 概率测度，简称概率。在离散形式下满足：

\[P(\mathcal{A})=\sum_{\omega \in \mathcal{A}}p(\omega) \]

其中 \(p(\omega)\) 是概率质量函数(相对于概率密度函数)。

2.1.3 随机过程

设在概率空间 \((\Omega,\mathcal{F},P)\) 上，对于一个指标集合 \(T\) 的任意元素 \(t \in T\)，均定义有一个随机变量 \(\xi_t(\omega)\)，则变量族 \(\{\xi_t(\omega)|t\in T\}\) 称为随机过程。指标集合 \(T\) 一般为整数集或实数集。

由于本文只研究离散时间的随机过程，可以取 \(T=\mathbb{N}\)。

2.2鞅与停时问题

2.2.1 鞅

若随机过程 \(X=\{X_n,n\ge 0\}\) 称为鞅，则满足：

  • 对 \(\forall n \ge 0\)，有 \(E(|X_n|)<\infty\)。
  • 对 \(\forall n \ge 0\)，有 \(E(X_{n+1}|X_0,X_1,\cdots,X_n)=X_n\)。

其中 \(E(X|Y)\) 表示条件期望。

从直观上，如果把随机变量的下标表示为时间，已知之前所有观测值，若下一次观测值的条件期望等于本次观测值，则称这一随机过程（即随机变量序列）是离散时间鞅。

更一般地，若随机过程 \(Y=\{Y_n|n\ge 0\}\) 满足：

  • 对 \(\forall n \ge 0\)，有 \(E(|Y_n|)<\infty\)。
  • 对 \(\forall n \ge 0\)，有 \(E(Y_{n+1}|X_0,X_1,\cdots,X_n)=Y_n\)。

则称随机过程 \(Y\) 是 \(X\) 的鞅。

2.2.2 停时

若对于一个随机过程 \(X=\{X_n,n\ge 0\}\)，随机变量 \(T\) 为非负整数，而事件 \({T=n}\) 的指示函数 \(I_{t=n}(X)\) 只与 \(X_0,X_1,\cdots,X_n\) 有关，则称 \(T\) 为随机过程 \(X\) 的随机时刻。

并且，若随机时刻 \(T\) 同时满足 \(P(T<\infty )=1\)，则称 \(T\) 为随机过程 \(X\) 的停时。

2.2.3 停止过程

若 \(T\) 是随机过程 \(X=\{X_n|n\ge 0\}\) 的停时，且令

\[\bar{X_n}= \begin{cases} X_n&n\le T\\ X_T&n>T \end{cases} \]

则称 \(\{\bar{X_n}\}\) 为停止过程。

容易证明，若 \(X\) 是鞅，则 \(\bar{X}\) 也是鞅。

2.2.4 停时定理

设 \(X=\{X_n|n\ge 0\}\) 是一个离散时间鞅，\(T\in \mathbb{N}\cup\infty\) 是停时，若下列条件之一成立：

  • \(T\) 有界。
  • \(\bar{X_n}\) 一致有界。
  • \(E(T)<\infty\) 且\(E(|X_{n+1}-X_n||X_0,\cdots,x_n)\) 有界。

则有

\[E(X_T)=E(X_0) \]

更一般地，若 \(\mathcal{F}=\{\mathcal{F}_n|n\ge 0\}\) 是一个非降\(\sigma\)-代数族，\(X=\{X_n|n\ge 0\}\)，\(X\) 与 \(T\) 是关于 \(\mathcal{F}\) 的鞅和停时，则若有下列条件之一成立：

  • \(T\) 几乎处处有界。
  • 存在 \(c\in\mathbb{N}\) 使得 \(\forall T\in \mathbb{N}\)，\(|X_{n\cap T}\le c|\) 几乎处处成立。
  • \(E(T)<\infty\) 且存在 \(M<\infty\) 使得 \(E(|X_{n+1}-X_n||\mathcal{F}_n)<M\)。

则有

\[E(X_T)=E(X_0) \]

鞅的停时定理说明，即使随机过程非常复杂，甚至可能趋向无穷，只要满足某些条件，
那么还是可以得到终态的某些性质。

3 一类图上随机游走问题

3.1 图上随机游走

一个图上随机游走问题可以用一个四元组 \((V,E,S,T)\) 描述，其中 \(V\) 是一个集合，表示图的节点；\(E\) 是 \(V\) 上的一个二元关系，表示图的边；\(S\)，\(T\) 均是 \(V\) 中的元素，分别表示游走的起始节点与终止节点。

设随机过程 \(X=\{X_n,n\ge 0\}\) 表示时刻 \(n\) 游走到的节点，满足：

  • \(X_0=S\)。
  • \(P(X_{n+1}=x|X_0,\cdots,X_n)=\begin{cases}\frac{1}{|\mathcal{E}_{X_n}|}&x\in\mathcal{E}_{X_n}\\0&\texttt{others}\end{cases}\)

其中 \(\mathcal{E}_u=\bigcup\limits_{\langle u,v\rangle\in E}\{v\}\)。表示 \(x\) 的所有出边对应的节点集合。

则随机过程 \(X_n\) 称为图上随机游走 \((V,E,S,T)\)。

3.1.1 图上随机游走的停时

若图上随机游走 \(X=(V,E,S,T)\) ，则随机变量 \(D=\min\limits_{X_n=T}\{n\}\) 称为随机游走 \(X\) 的停时。具体问题中，一般只关注停时的数学期望 \(E(D)\)。

3.2 计算停时的通用方法

设随机过程 \(X=\{X_n|n\ge 0\}\) 的停时为 \(T\)。直接计算 \(E(T)\) 通常比较困难。

考虑构造势函数 \(\phi(x)\) 满足：

  • \(E(\phi(X_{n+1})-\phi(X_n)|X_0,\cdots,X_n)=-1\)。
  • \(\phi(X_T)<\infty\)。

令 \(Y_n=\phi(X_n)+n\)，则有

\[E(Y_{n+1}|Y_0,\cdots,Y_n)=Y_n \]

即 \(Y=\{Y_n|n\ge 0\}\) 是鞅，根据停时定理有

\[E(Y_T)=E(Y_0) \]

即

\[E(T)=\phi(X_0)-\phi(X_T) \]

3.3 部分特殊图上随机游走停时的计算

3.3.1 例1

设一个有 \(n+1\) 个节点的图编号为 \(1\) 到 \(n+1\)，对于编号小于等于 \(n\) 的节点均有一个自环和一条到 \(n+1\) 的边，形如

该图上随机游走 \(1\) 到 \(n+1\) 的停时记作 \(T\)。

构造 \(\phi(n)=-2n\)。

\[\begin{align*} E(\phi(X_{n+1})-\phi(X_{n})|X_0,\cdots,X_n)&=\frac{1}{2}(-2n-2(n+1))-(-2n)\\ &=-1 \end{align*} \]

所以 \(E(T)=\phi(0)-\phi(n)=2n\)。

3.3.2 例2

在例1的基础上将除了1号节点的自环改为向 \(n-1\) 的边，形如

同理，构造 \(\phi(n)=-n(n+1)\)。

\[\begin{align*} E(\phi(X_{n+1})-\phi(X_{n})|X_0,\cdots,X_n)&=\frac{1}{2}(-(n+1)(n+2)-2(n-1)n)+n(n+1)\\ &=-1 \end{align*} \]

所以 \(E(T)=\phi(0)-\phi(n)=n(n+1)\)。

3.3.3 例3

在例1的基础上将自环改为向1号节点的边，形如

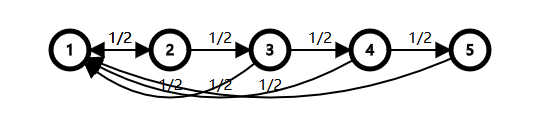
构造 \(\phi(n)=2-2^{n+1}\)。

\[\begin{align*} E(\phi(X_{n+1})-\phi(X_{n})|X_0,\cdots,X_n)&=\frac{1}{2}(-(2-2^1)-(2-2^{n+2})-(2-2^{n+1})\\ &=-1 \end{align*} \]

所以 \(E(T)=\phi(0)-\phi(n)=2^{n+1}-2\)。

3.4 更一般的结论

设在一条长度为 \(n+1\) 的链的基础上，还有若干条返祖边 \(\langle u,v\rangle\) 满足 \(u\le v\)。由于每个节点的出边情况并不相同，所以 势函数 \(\phi(x)\) 很难直接写出。

但为了构造使得 \(\phi(X_n)+n\) 是鞅，我们可以知道：

\[\begin{align*} E(\phi(X_{n+1})-\phi(X_n)|X_0,\cdots,X_n) &= \frac{1}{|\mathcal{E}_{X_n}|}\sum_{x\in \mathcal{E}_{X_n}}\left(\phi(X_n)-\phi(x)\right) \\ &= \phi(X_n)-\frac{1}{|\mathcal{E}_{X_n}|}\sum_{x\in \mathcal{E}_{X_n}}\phi(x))\\ &= -1 \end{align*} \]

又 \(X_{n}+1 \in \mathcal{E}_{X_n}\)，所以

\[\phi(n+1)=\phi(n)+|\mathcal{E}_{n}|+\sum\limits_{x\in\mathcal{E}_n,x\neq n+1}(\phi(n)-\phi(x)) \]

令 \(\phi(1)=0\)，于是有递推式

\[E(T)=\phi(n+1)= \begin{cases} 0&n=1\\ (\phi(n)+1)|\mathcal{E}n|-\sum\limits_{x\in\mathcal{E}_n,x\neq n + 1}\phi(x)&n>1 \end{cases} \]

References

posted @ 2021-12-14 15:02  _bzy  阅读(850)  评论(0)  编辑  收藏  举报