洛谷P4151 [WC2011]最大XOR和路径（线性基）

传送门

 

 

不知道线性基是什么东西的可以看看蒟蒻的总结

首先看到异或就想到线性基

我们考虑有一条路径，那么从这条路径走到图中的任意一个环再走回这条路径上，对答案的贡献是这个环的异或和，走到这个环上的路径对答案是没有影响的

以这张（偷来的）图为例

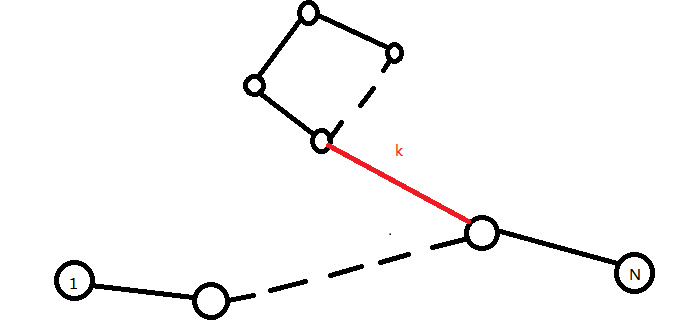
从$1$走到$n$，先走到环再走回来，那么到环上那条路径（红色的）被走了两次，那么异或之后为0，对答案无贡献

那么我们可以随意走一条路径，然后把图上所有环丢到线性基里，求一下在这些线性基下最大能异或和是多少，就是个板子了

那么考虑一下走的路径会不会对答案有影响

依然考虑（盗来的）图

一开始走的是$B$这条路径，但实际上$A$更优，那么$B$路径异或上这整个大环的权值就是$A$路径的权值

找环可以直接dfs

然后没有然后了

//minamoto
#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
inline ll read(){
    #define num ch-'0'
    char ch;bool flag=0;ll res;
    while(!isdigit(ch=getc()))
    (ch=='-')&&(flag=true);
    for(res=num;isdigit(ch=getc());res=res*10+num);
    (flag)&&(res=-res);
    #undef num
    return res;
}
ll b[65];
void insert(ll x){
    for(int i=63;i>=0;--i){
        if((x>>i)&1){
            if(!b[i]){
                b[i]=x;return;
            }
            x^=b[i];
        }
    }
}
ll query(ll x){
    ll res=x;
    for(int i=63;i>=0;--i)
    if((res^b[i])>res) res^=b[i];
    return res;
}
const int N=5e4+5,M=2e5+5;
int head[N],Next[M],ver[M],tot;ll edge[M];
inline void add(int u,int v,ll e){
    ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e;
}
int vis[N];ll del[N];
void dfs(int u,ll res){
    del[u]=res,vis[u]=1;
    for(int i=head[u];i;i=Next[i])
    if(!vis[ver[i]]) dfs(ver[i],res^edge[i]);
    else insert(res^edge[i]^del[ver[i]]);
}
int main(){
//    freopen("testdata.in","r",stdin);
    int n,m,u,v;ll e;n=read(),m=read();
    for(int i=1;i<=m;++i)
    u=read(),v=read(),e=read(),add(u,v,e),add(v,u,e);
    dfs(1,0);
    printf("%lld\n",query(del[n]));
    return 0;
}