点分治&&动态点分治学习笔记
突然发现网上关于点分和动态点分的教程好像很少……蒟蒻开篇blog记录一下吧……因为这是个大傻逼,可能有很多地方写错,欢迎在下面提出
参考文献:https://www.cnblogs.com/LadyLex/p/8006488.html
https://blog.csdn.net/qq_39553725/article/details/77542223
https://blog.csdn.net/zzkksunboy/article/details/70244945
前言
一般来说,对于大规模处理树上路径,我们会对整棵树进行分治。而树分治有两种,一种是边分治,不在本文考虑范围内(主要是我不会)所以暂且不提,另外一种就是点分治。
淀粉质,啊呸,点分治,顾名思义,就是把树上的节点拆开来进行分治,每一次把树给拆成好几棵子树,然后再继续递归下去,直到算出所有的答案
分治点
既然是分治,我们肯定每一次都要选择一个点,从他开始分治下去。那么考虑我们如何选择这个点呢?我们发现,每一次处理完一个点之后,我们都要递归进它的子树,那么时间复杂度受到它最大的子树的大小的影响。比如,如果原树是一条链,我们选择链首,一路递归下去,时间复杂度毫无疑问是$O(n^2)$的(那还不如别学了直接打暴力)。所以,我们要让每一次选到的点的最大子树最小。
实际上,一棵树的最大子树最小的点有一个名称,叫做重心。
时间复杂度
考虑一下为什么每一次都选择重心,时间复杂度就是对的呢?
因为重心有一个很重要的性质,每一个子树的大小都不超过$n/2$
考虑为什么呢?我们可以用反证法来证明(这里感谢zzk大佬的证明)
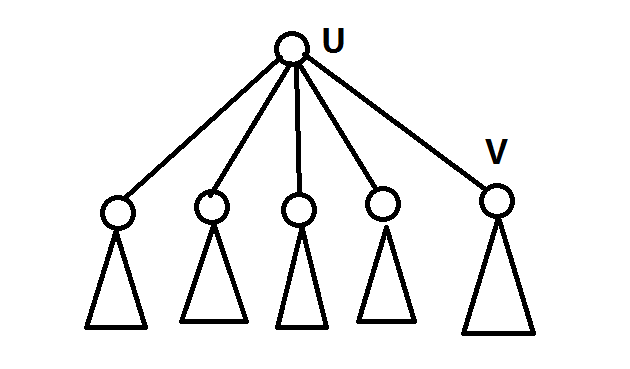
考虑有如上这么一棵树,其中点$u$是重心,$son[u]$表示$u$点的最大的子树的大小,$v$是点$u$的最大子树,且$size[v]>size[u]/2$
因为$size[v]>size[u]/2$,其他子树加上点$u$的节点数小于$size[u]/2$,那么不难发现,我们选择点$v$作为重心,$son[v]=size[v]-1<son[u]$,那么很明显$u$不满足重心的定义
于是每一次找到重心,递归的子树大小是不超过原树大小的一半的,那么递归层数不会超过$O(logn)$层,时间复杂度为$O(nlogn)$
求重心
然而重心如何求呢?直接暴力,我们$dfs$整棵树,可以$O(n)$的求出树的重心
还是贴代码好了
void findrt(int u,int fa){ //sz表示子树的大小,son表示点的最大子树的大小 //cmax(a,b)表示如果b>a则a=b //个人习惯这样写,或者直接写成a=max(a,b) sz[u]=1,son[u]=0; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]||v==fa) continue; findrt(v,u); sz[u]+=sz[v]; cmax(son[u],sz[v]); } //size表示整棵树的大小 //因为这是一棵无根树,所以包括它的父亲在内的那一坨也应该算作它的子树 cmax(son[u],size-sz[u]); if(son[u]<mx) mx=son[u],rt=u; }
于是就可以愉快的$O(n)$求出重心(~ ̄▽ ̄)~
实现
还是先贴代码好了
void divide(int u){ ans+=solve(u,0);//把当前节点的答案加上去 vis[u]=1;//把节点标记,防止陷入死循环 for(int i=head[u];i;i=Next[i]){ //分别处理每一棵子树 int v=ver[i]; if(vis[v]) continue; ans-=solve(v,edge[i]);//容斥原理,下面说 mx=inf,rt=0,size=sz[v]; //把所有信息更新,递归进子树找重心,并继续分治 findrt(v,0); divide(rt); } }
上面其他的应该都好理解,除了这一句 ans-=solve(v,edge[i]);
考虑一下这棵树
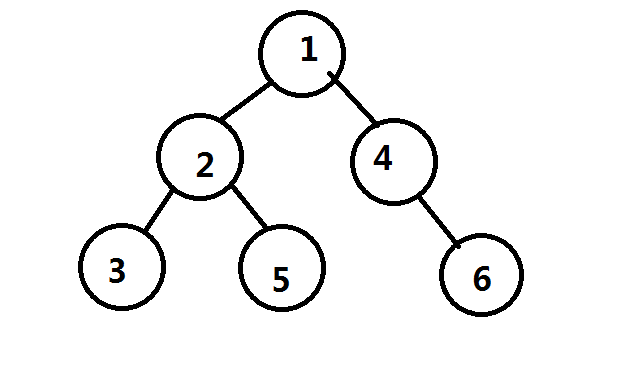
考虑一下,从点$1$出发的路径有以下几条
$1->4$
$1->4->6$
$1->2$
$1->2->3$
$1->2->5$
然后我们为了求贡献,会将路径两两合并
然而合并$1->2->3$和$1->2->5$这两条路径实际上是不合法的,因为出现了重边
所以要减去$2$这一棵子树中的所有路径两两合并的贡献
然后回头来看代码 ans+=solve(u,0); ans-=solve(v,edge[i]);
看到没?第二个参数不一样,这样在考虑子树中两两合并时的贡献时就不会把这一条边的贡献给漏掉了
然后只要递归继续找就可以(*^▽^*)
注意点
实际上呢,点分的时候找重心的写法有两种,一种是上面的那个,另一种我贴上来,就是在递归的时候写的不一样
1 void divide(int u){ 2 ans+=solve(u,0); 3 vis[u]=1; 4 int totsz=size; 5 for(int i=head[u];i;i=Next[i]){ 6 int v=ver[i]; 7 if(vis[v]) continue; 8 ans-=solve(v,edge[i]); 9 mx=inf,rt=0; 10 size=sz[v]>sz[u]?totsz-sz[u]:sz[v];//这里应该这样写才是对的 11 findrt(v,0); 12 divide(rt); 13 } 14 }
实际上这一种方法才是对的,我上面写的反而是错的,然而时间复杂度并不会退化,具体的证明请看->这里
例题
讲了这么多……然而实际上似乎并没有什么用……还是来讲几道题好了……

//minamoto #include<bits/stdc++.h> #define N 40005 #define M 80005 #define ll long long #define inf 0x3f3f3f3f using namespace std; #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<15,stdin),p1==p2)?EOF:*p1++) char buf[1<<15],*p1=buf,*p2=buf; template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} inline int read(){ #define num ch-'0' char ch;bool flag=0;int res; while(!isdigit(ch=getc())) (ch=='-')&&(flag=true); for(res=num;isdigit(ch=getc());res=res*10+num); (flag)&&(res=-res); #undef num return res; } int ver[M],Next[M],head[N],edge[M]; int n,tot,root;ll k; void add(int u,int v,int e){ ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e; } int sz[N],vis[N],mx,size; ll d[N],q[N],l,r; void getroot(int u,int fa){ sz[u]=1;int num=0; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(v==fa||vis[v]) continue; getroot(v,u); sz[u]+=sz[v]; cmax(num,sz[v]); } cmax(num,size-sz[u]); if(num<mx) mx=num,root=u; } void getdis(int u,int fa){ q[++r]=d[u]; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(v==fa||vis[v]) continue; d[v]=d[u]+edge[i]; getdis(v,u); } } ll calc(int u,int val){ r=0; d[u]=val; getdis(u,0); ll sum=0;l=1; sort(q+1,q+r+1); while(l<r){ if(q[l]+q[r]<=k) sum+=r-l,++l; else --r; } return sum; } ll ans=0; void dfs(int u){ ans+=calc(u,0); vis[u]=1; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]) continue; ans-=calc(v,edge[i]); size=sz[v]; mx=inf; getroot(v,0); dfs(root); } } int main(){ //freopen("testdata.in","r",stdin); n=read(); for(int i=1;i<n;++i){ int u=read(),v=read(),e=read(); add(u,v,e); } k=read(); size=n; mx=inf; getroot(1,0); dfs(root); printf("%lld",ans); return 0; }
poj1741tree
给一颗n个节点的树,每条边上有一个距离v。定义d(u,v)为u到v的最小距离。给定k值,求有多少点对(u,v)使u到v的距离小于等于k。
点分的板子……好像基本都是板子套进去……就是注意合并的时候二分保证复杂度
bzoj2152 聪聪可可
题目描述
聪聪和可可是兄弟俩,他们俩经常为了一些琐事打起来,例如家中只剩下最后一根冰棍而两人都想吃、两个人都想玩儿电脑(可是他们家只有一台电脑)……遇到这种问题,一般情况下石头剪刀布就好了,可是他们已经玩儿腻了这种低智商的游戏。
他们的爸爸快被他们的争吵烦死了,所以他发明了一个新游戏:由爸爸在纸上画n个“点”,并用n-1条“边”把这n个“点”恰好连通(其实这就是一棵树)。并且每条“边”上都有一个数。接下来由聪聪和可可分别随即选一个点(当然他们选点时是看不到这棵树的),如果两个点之间所有边上数的和加起来恰好是3的倍数,则判聪聪赢,否则可可赢。
聪聪非常爱思考问题,在每次游戏后都会仔细研究这棵树,希望知道对于这张图自己的获胜概率是多少。现请你帮忙求出这个值以验证聪聪的答案是否正确。
输入输出格式
输入格式:
输入的第1行包含1个正整数n。后面n-1行,每行3个整数x、y、w,表示x号点和y号点之间有一条边,上面的数是w。
输出格式:
以即约分数形式输出这个概率(即“a/b”的形式,其中a和b必须互质。如果概率为1,输出“1/1”)。
输入输出样例
说明
【样例说明】
13组点对分别是(1,1) (2,2) (2,3) (2,5) (3,2) (3,3) (3,4) (3,5) (4,3) (4,4) (5,2) (5,3) (5,5)。
【数据规模】
对于100%的数据,n<=20000。
很明显,思路就是统计长度为$3$的倍数的路径的条数,然后除以路径总和就是答案
先贴一句话题解:先用点分计算出路径长度,把路径长度对$3$取模,然后用$sum[1],sum[2],sum[0]$表示模数是$1,2,3$的情况的总数,那么就是$ans+=sum[1]*sum[2]*2+sum[0]*sum[0]$,最后答案就是$ans/(n*n)$
用人话说的话,我们可以先考虑一个点,用$sum[1,2,3]$分别表示从以这一个点为根,往下的长度对$3$取模余数是$1,2,3$的路径条数,那么所有经过这一个点的路径有多少条呢?所有长度为$1$和$2$的路径可以两两拼起来成为一条,反着也可以,长度为$3$的路径可以两两拼。所以答案就加上上面那个式子
然后进行点分,不断递归就可以了

1 //minamoto 2 #include<iostream> 3 #include<cstdio> 4 #define ll long long 5 #define inf 0x3f3f3f3f 6 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 7 char buf[1<<21],*p1=buf,*p2=buf; 8 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} 9 inline int read(){ 10 #define num ch-'0' 11 char ch;bool flag=0;int res; 12 while(!isdigit(ch=getc())) 13 (ch=='-')&&(flag=true); 14 for(res=num;isdigit(ch=getc());res=res*10+num); 15 (flag)&&(res=-res); 16 #undef num 17 return res; 18 } 19 char sr[1<<21],z[20];int C=-1,Z; 20 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 21 inline void print(int x){ 22 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 23 while(z[++Z]=x%10+48,x/=10); 24 while(sr[++C]=z[Z],--Z); 25 } 26 const int N=20005,mod=3; 27 int head[N],Next[N<<1],edge[N<<1],ver[N<<1];ll ans=0; 28 int sz[N],son[N],sum[4],vis[N]; 29 int size,mx,rt,n,tot; 30 inline void add(int u,int v,int e){ 31 ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; 32 ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e; 33 } 34 void getrt(int u,int fa){ 35 sz[u]=1,son[u]=0; 36 for(int i=head[u];i;i=Next[i]){ 37 int v=ver[i]; 38 if(vis[v]||v==fa) continue; 39 getrt(v,u); 40 sz[u]+=sz[v]; 41 cmax(son[u],sz[v]); 42 } 43 cmax(son[u],size-sz[u]); 44 if(son[u]<mx) mx=son[u],rt=u; 45 } 46 void query(int u,int fa,int d){ 47 ++sum[d%mod]; 48 for(int i=head[u];i;i=Next[i]){ 49 int v=ver[i]; 50 if(vis[v]||v==fa) continue; 51 query(v,u,(d+edge[i])%mod); 52 } 53 } 54 ll solve(int rt,int d){ 55 sum[0]=sum[1]=sum[2]=0; 56 query(rt,0,d); 57 ll res=1ll*sum[1]*sum[2]*2+1ll*sum[0]*sum[0]; 58 return res; 59 } 60 void divide(int u){ 61 ans+=solve(u,0); 62 vis[u]=1; 63 for(int i=head[u];i;i=Next[i]){ 64 int v=ver[i]; 65 if(vis[v]) continue; 66 ans-=solve(v,edge[i]); 67 mx=inf,rt=0,size=sz[v]; 68 getrt(v,0); 69 divide(rt); 70 } 71 } 72 inline ll gcd(ll a,ll b){ 73 while(b^=a^=b^=a%=b); 74 return a; 75 } 76 int main(){ 77 n=read(); 78 for(int i=1;i<n;++i){ 79 int u=read(),v=read(),e=read(); 80 add(u,v,e%3); 81 } 82 mx=inf,size=n,ans=0,rt=0; 83 getrt(1,0),divide(rt); 84 ll p=n*n,GCD=gcd(ans,p); 85 print(ans/GCD),sr[++C]='/',print(p/GCD); 86 Ot(); 87 return 0; 88 }
洛谷P3806 【模板】点分治1
题目描述
给定一棵有n个点的树
询问树上距离为k的点对是否存在。
输入输出格式
输入格式:
n,m 接下来n-1条边a,b,c描述a到b有一条长度为c的路径
接下来m行每行询问一个K
输出格式:
对于每个K每行输出一个答案,存在输出“AYE”,否则输出”NAY”(不包含引号)
输入输出样例
说明
对于30%的数据n<=100
对于60%的数据n<=1000,m<=50
对于100%的数据n<=10000,m<=100,c<=1000,K<=10000000
考虑一下$k$的范围,干脆预处理出答案然后直接$O(1)$回答询问吧……
就是把每一个节点向下长度为$d$的路径有多少条记下来,然后两两合并,时间复杂度$O(n^2)$,不知道为毛能过……

//minamoto #include<cstdio> #include<iostream> #define inf 0x3f3f3f3f #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) char buf[1<<21],*p1=buf,*p2=buf; template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} inline int read(){ #define num ch-'0' char ch;bool flag=0;int res; while(!isdigit(ch=getc())) (ch=='-')&&(flag=true); for(res=num;isdigit(ch=getc());res=res*10+num); (flag)&&(res=-res); #undef num return res; } const int N=10005; int ans[10000005]; int ver[N<<1],head[N],Next[N<<1],edge[N<<1]; int sz[N],son[N],st[N];bool vis[N]; int n,m,size,mx,rt,tot,top; inline void add(int u,int v,int e){ ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e; } void getrt(int u,int fa){ sz[u]=1,son[u]=0; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]||v==fa) continue; getrt(v,u); sz[u]+=sz[v],cmax(son[u],sz[v]); } cmax(son[u],size-sz[u]); if(son[u]<mx) mx=son[u],rt=u; } void query(int u,int fa,int d){ st[++top]=d; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]||v==fa) continue; query(v,u,d+edge[i]); } } void solve(int rt,int d,int f){ top=0; query(rt,0,d); if(f){ for(int i=1;i<top;++i) for(int j=i+1;j<=top;++j) ++ans[st[i]+st[j]]; } else{ for(int i=1;i<top;++i) for(int j=i+1;j<=top;++j) --ans[st[i]+st[j]]; } } void divide(int u){ vis[u]=true; solve(u,0,1); for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]) continue; solve(v,edge[i],0); mx=inf,rt=0,size=sz[v]; getrt(v,0); divide(rt); } } int main(){ n=read(),m=read(); for(int i=1;i<n;++i){ int u=read(),v=read(),e=read(); add(u,v,e); } rt=0,mx=inf,size=n; getrt(1,0),divide(rt); while(m--){ int k=read(); puts(ans[k]?"AYE":"NAY"); } return 0; }
然后就是关于点分的一些题单了,基本我都写(chao)了题解的
洛谷P2664 树上游戏(点分治)------------->蒟蒻的题解
[IOI2011]Race (点分治)(洛谷地址)------------->蒟蒻的题解
动态点分治
一般来说,点分治只能处理静态的问题
然而如果题目要求待修改怎么办哩?(当然是修改一次做一次点分,多省事)
这个时候就需要动态点分治大显身手啦
我们可以对树中的每一个点维护一个数组或者数据结构,然后通过维护它们来完成状态之间的转移
然而一条链就可以送我们上天……
我们考虑一下,整棵树的结构是不变的(如果变了那就是LCT的范围了),被修改的只有点权。那么,我们每一次进行点分时选到的重心也是不变的。
下面给出点分树的定义:把点分治时每一层的重心之间连边,这就构成了一颗高度为$logn$的新树,我们叫它分治树。
用人话说的话,就是我们每一次点分完一棵树,会继续往子树里点分,那么我们可以把这一次的重心和子树里的重心连边。因为点分的递归层数最多只有$logn$层,所以这棵树高度为$logn$
八成还是没解释清楚(毕竟我不太对的起语文老师),来画个图吧,这是一棵树,重心是点$1$
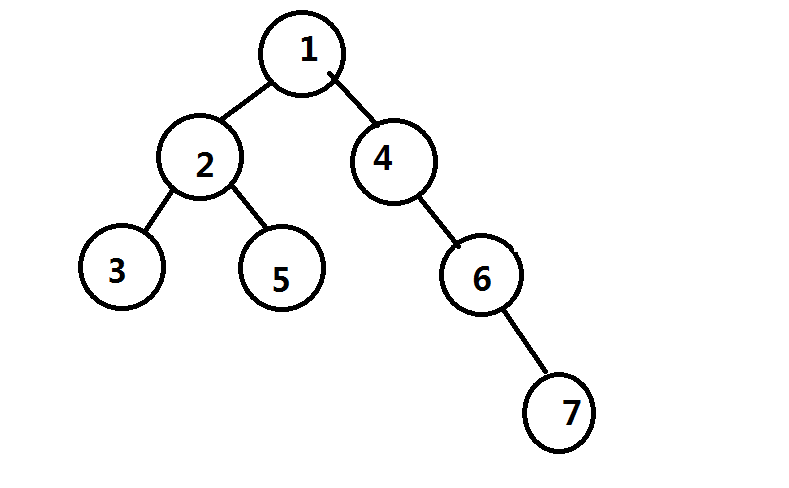
我们假设已经处理完了所有经过点$1$的路径,然后递归进子树继续点分,那么实际上原树被拆成了这么两棵树,两个重心分别为$2$和$6$
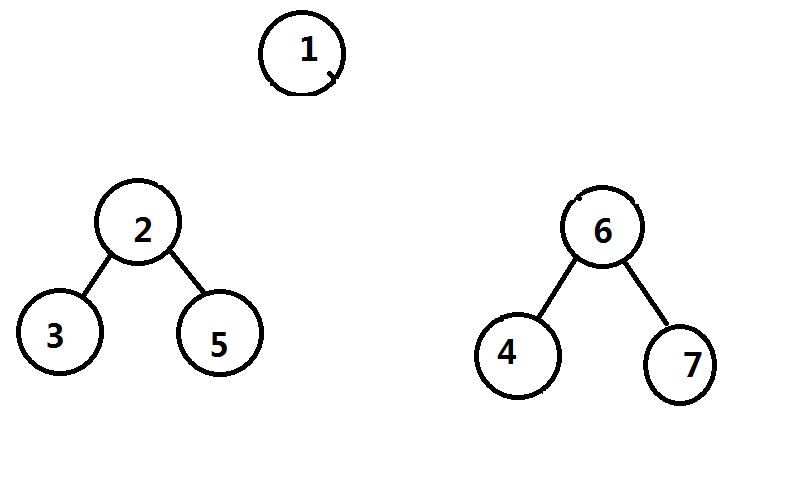
那么把第一层的重心和第二层的重心给连接起来(用红色表示)
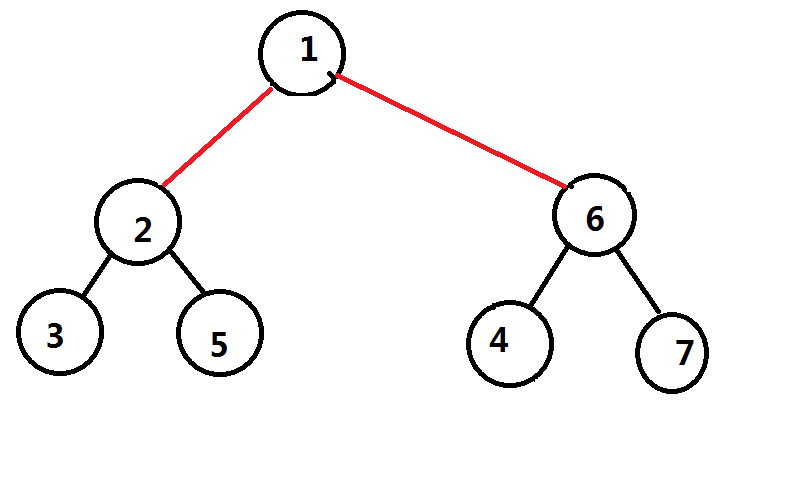
然后我们继续进行点分,我们已经把经过点$2$和点$6$的所有路径都已经处理完了,那么子树又会继续拆分
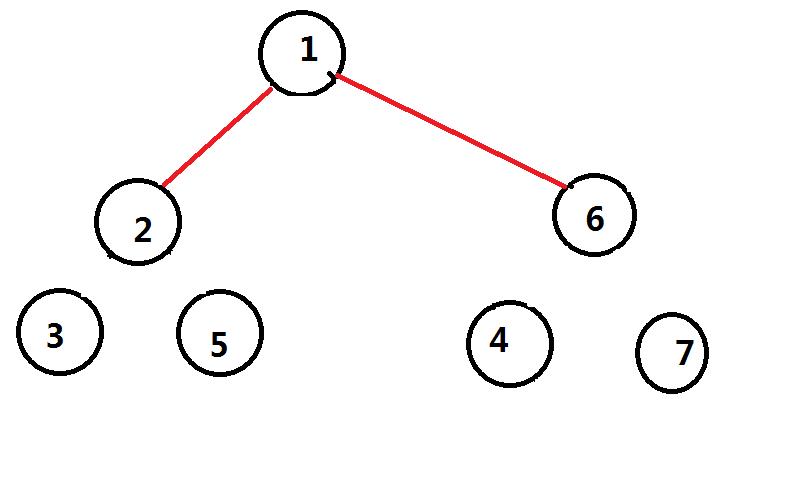
然后因为子树大小只有$1$,重心就是他们自己,继续和上一层的重心连边
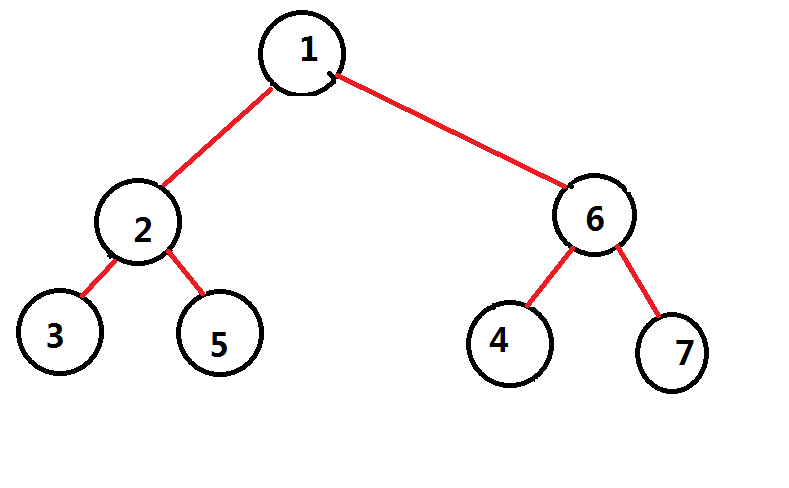
然后这一棵点分树就建好了
贴代码(事实上只是在原先的板子上加了一句话而已,就是那句 fa[rt]=u )
那么每一次修改,只要在点分树里不断往上跳,就能够维护整棵树的信息了
void solve(int u){ vis[u]=true;int totsz=size; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]) continue; rt=0,son[0]=n+1; size=sz[v]>sz[u]?totsz-sz[u]:sz[v]; findrt(v,0),fa[rt]=u,solve(rt); //事实上,我们只需要记录点分树上的父亲即可(一般情况下) } }
然后基本的介绍就到这里……似乎还是太抽象了……还是来讲几道题目吧
「BZOJ1095」[ZJOI2007] Hide 捉迷藏
题目描述
Jiajia和Wind是一对恩爱的夫妻,并且他们有很多孩子。某天,Jiajia、Wind和孩子们决定在家里玩捉迷藏游戏。他们的家很大且构造很奇特,由N个屋子和N-1条双向走廊组成,这N-1条走廊的分布使得任意两个屋子都互相可达。
游戏是这样进行的,孩子们负责躲藏,Jiajia负责找,而Wind负责操纵这N个屋子的灯。在起初的时候,所有的灯都没有被打开。每一次,孩子们只会躲藏在没有开灯的房间中,但是为了增加刺激性,孩子们会要求打开某个房间的电灯或者关闭某个房间的电灯。为了评估某一次游戏的复杂性,Jiajia希望知道可能的最远的两个孩子的距离(即最远的两个关灯房间的距离)。
我们将以如下形式定义每一种操作:
- C(hange) i 改变第i个房间的照明状态,若原来打开,则关闭;若原来关闭,则打开。
- G(ame) 开始一次游戏,查询最远的两个关灯房间的距离。
输入输出格式
输入格式:
第一行包含一个整数N,表示房间的个数,房间将被编号为1,2,3…N的整数。
接下来N-1行每行两个整数a, b,表示房间a与房间b之间有一条走廊相连。
接下来一行包含一个整数Q,表示操作次数。接着Q行,每行一个操作,如上文所示。
输出格式:
对于每一个操作Game,输出一个非负整数到hide.out,表示最远的两个关灯房间的距离。若只有一个房间是关着灯的,输出0;若所有房间的灯都开着,输出-1。
输入输出样例
说明
对于20%的数据, N ≤50, M ≤100;
对于60%的数据, N ≤3000, M ≤10000; 对于100%的数据, N ≤100000, M ≤500000。
动态点分治的板子题
(然而我该说我当初做这道题是抄了岛娘和hzwer的括号序列么……因为看着觉得代码比较好抄……所以根本没打过动态点分的板子……)
我就直接说一下思路(然后随便放个别的大佬的代码好了)
我们考虑一下,在每一个点需要维护这一个点在点分树中往下延伸到黑点的所有长度,然后每一次都把最长的和次长的给连接起来
这个可以每一个节点开一个大根堆
然而如果两条链是来自同一棵子树的就GG了……
那么可以再开一个堆,维护这一个点的所有儿子的堆顶,然后每一次取出的最长和次长可以保证不是在同一棵子树里
然后再开一个堆维护一下每一个节点的答案……
考虑修改怎么操作?每一次在第一个堆里进行修改,维护第二个堆和第三个堆就可以了
分治树深度$logn$,堆操作时间复杂度是$logn$,总时间复杂度是$O(nlog^2n)$
然后放一下LadyLex大佬的代码吧(才不是因为我懒得打呢)

1 #include <cstdio> 2 #include <cstring> 3 #include <ctime> 4 #include <set> 5 #include <queue> 6 using namespace std; 7 #define N 100010 8 #define inf 0x3fffffff 9 #define Vt Vater[rt] 10 int n,e,adj[N]; 11 struct edge{int zhong,next;}s[N<<1]; 12 inline void add(int qi,int zhong) 13 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 14 int Vater[N],size[N],root,totsize,maxs[N]; 15 bool state[N],vis[N]; 16 #define max(a,b) ((a)>(b)?(a):(b)) 17 #define min(a,b) ((a)<(b)?(a):(b)) 18 struct heap 19 { 20 priority_queue<int>q1,q2; 21 inline void push(int x){q1.push(x);} 22 inline void erase(int x){q2.push(x);} 23 inline int top() 24 { 25 while(q2.size()&&q1.top()==q2.top())q1.pop(),q2.pop(); 26 return q1.top(); 27 } 28 inline void pop() 29 { 30 while(q2.size()&&q1.top()==q2.top())q1.pop(),q2.pop(); 31 q1.pop(); 32 } 33 inline int top2() 34 { 35 int val=top();pop(); 36 int ret=top();push(val); 37 return ret; 38 } 39 inline int size() 40 { 41 return q1.size()-q2.size(); 42 } 43 }h1[N],h2[N],h3; 44 inline void dfs1(int rt,int fa) 45 { 46 size[rt]=1,maxs[rt]=0; 47 for(int i=adj[rt];i;i=s[i].next) 48 if(s[i].zhong!=fa&&!vis[s[i].zhong]) 49 dfs1(s[i].zhong,rt),size[rt]+=size[s[i].zhong], 50 maxs[rt]=max(maxs[rt],size[s[i].zhong]); 51 maxs[rt]=max(maxs[rt],totsize-maxs[rt]); 52 if(maxs[rt]<maxs[root])root=rt; 53 } 54 int f[N][18],bin[25],tp,deep[N]; 55 inline void pre(int rt,int fa) 56 { 57 f[rt][0]=fa;deep[rt]=deep[fa]+1; 58 for(int i=1;bin[i]+1<=deep[rt];++i)f[rt][i]=f[f[rt][i-1]][i-1]; 59 for(int i=adj[rt];i;i=s[i].next) 60 if(s[i].zhong!=fa)pre(s[i].zhong,rt); 61 } 62 inline int LCA(int a,int b) 63 { 64 if(deep[a]<deep[b])a^=b,b^=a,a^=b; 65 int i,cha=deep[a]-deep[b]; 66 for(i=tp;~i;--i)if(cha&bin[i])a=f[a][i]; 67 if(a==b)return a; 68 for(i=tp;~i;--i) 69 if(f[a][i]!=f[b][i])a=f[a][i],b=f[b][i]; 70 return f[a][0]; 71 } 72 inline int dis(int a,int b) 73 {return deep[a]+deep[b]-(deep[LCA(a,b)]<<1);} 74 inline void dfs3(int rt,int fa,int Vatty) 75 { 76 h1[root].push(dis(rt,Vatty)); 77 for(int i=adj[rt];i;i=s[i].next) 78 if(!vis[s[i].zhong]&&s[i].zhong!=fa) 79 dfs3(s[i].zhong,rt,Vatty); 80 } 81 inline void dfs2(int rt,int fa) 82 { 83 Vt=fa,vis[rt]=1,h2[rt].push(0); 84 int siz=totsize; 85 for(int i=adj[rt];i;i=s[i].next) 86 if(!vis[s[i].zhong]) 87 { 88 if(size[s[i].zhong]>size[rt]) 89 totsize=siz-size[rt]; 90 else 91 totsize=size[s[i].zhong]; 92 root=0,dfs1(s[i].zhong,0),dfs3(root,0,rt); 93 h2[rt].push(h1[root].top()),dfs2(root,rt); 94 } 95 if(h2[rt].size()>1)h3.push(h2[rt].top()+h2[rt].top2()); 96 } 97 inline void turnoff(int who) 98 { 99 int val,tmp; 100 if(h2[who].size()>1)h3.erase(h2[who].top()+h2[who].top2()); 101 h2[who].push(0); 102 if(h2[who].size()>1)h3.push(h2[who].top()+h2[who].top2()); 103 //queue empty() 后依然有数 104 for(int rt=who;Vt;rt=Vt) 105 { 106 if(h2[Vt].size()>1)h3.erase(h2[Vt].top()+h2[Vt].top2()); 107 if(h1[rt].size())h2[Vt].erase(h1[rt].top()); 108 h1[rt].push(dis(who,Vt)); 109 h2[Vt].push(h1[rt].top()); 110 if(h2[Vt].size()>1)h3.push(h2[Vt].top()+h2[Vt].top2()); 111 } 112 } 113 inline void turnon(int who) 114 { 115 int val,tmp; 116 if(h2[who].size()>1)h3.erase(h2[who].top()+h2[who].top2()); 117 h2[who].erase(0); 118 if(h2[who].size()>1)h3.push(h2[who].top()+h2[who].top2()); 119 //queue empty()后依然有数 120 for(int rt=who;Vt;rt=Vt) 121 { 122 if(h2[Vt].size()>1)h3.erase(h2[Vt].top()+h2[Vt].top2()); 123 h2[Vt].erase(h1[rt].top()); 124 h1[rt].erase(dis(who,Vt)); 125 if(h1[rt].size())h2[Vt].push(h1[rt].top()); 126 if(h2[Vt].size()>1)h3.push(h2[Vt].top()+h2[Vt].top2()); 127 } 128 } 129 char B[1<<15],X=0,*S=B,*T=B; 130 #define getc ( S==T&&( T=(S=B)+fread(B,1,1<<15,stdin),S==T )?0:*S++ ) 131 inline int read() 132 { 133 int x=0;while(X<'0'||X>'9')X=getc; 134 while(X>='0'&&X<='9')x=10*x+(X^48),X=getc; 135 return x; 136 } 137 inline void readc(){X=getc;while(X<'A'||X>'Z')X=getc;} 138 int main() 139 { 140 // freopen("hide1.in","r",stdin); 141 // freopen("hide.out","w",stdout); 142 n=read(); 143 register int i,j,q,a,b,cnt=n; 144 for(bin[0]=i=1;i<=20;++i)bin[i]=bin[i-1]<<1; 145 while(bin[tp+1]<=n)++tp; 146 for(i=1;i<n;++i) 147 a=read(),b=read(),add(a,b),add(b,a); 148 pre(1,0); 149 maxs[0]=inf,root=0,totsize=n,dfs1(1,0),dfs2(root,0); 150 q=read(); 151 while(q--) 152 { 153 readc(); 154 if(X=='C') 155 { 156 i=read(); 157 if(state[i])++cnt,turnoff(i); 158 else --cnt,turnon(i); 159 state[i]^=1; 160 } 161 else 162 { 163 if(cnt<2)printf("%d\n",cnt-1); 164 else printf("%d\n",h3.top()); 165 } 166 } 167 }
BZOJ 3924: [Zjoi2015]幻想乡战略游戏(动态点分治)
题目描述
傲娇少女幽香正在玩一个非常有趣的战略类游戏,本来这个游戏的地图其实还不算太大,幽香还能管得过来,但是不知道为什么现在的网游厂商把游戏的地图越做越大,以至于幽香一眼根本看不过来,更别说和别人打仗了。
在打仗之前,幽香现在面临一个非常基本的管理问题需要解决。 整个地图是一个树结构,一共有n块空地,这些空地被n-1条带权边连接起来,使得每两个点之间有一条唯一的路径将它们连接起来。
在游戏中,幽香可能在空地上增加或者减少一些军队。同时,幽香可以在一个空地上放置一个补给站。 如果补给站在点u上,并且空地v上有dv个单位的军队,那么幽香每天就要花费dv*dist(u,v)的金钱来补给这些军队。
由于幽香需要补给所有的军队,因此幽香总共就要花费为Sigma(Dv*dist(u,v),其中1<=V<=N)的代价。其中dist(u,v)表示u个v在树上的距离(唯一路径的权和)。
因为游戏的规定,幽香只能选择一个空地作为补给站。在游戏的过程中,幽香可能会在某些空地上制造一些军队,也可能会减少某些空地上的军队,进行了这样的操作以后,出于经济上的考虑,幽香往往可以移动他的补给站从而省一些钱。
但是由于这个游戏的地图是在太大了,幽香无法轻易的进行最优的安排,你能帮帮她吗? 你可以假定一开始所有空地上都没有军队。
输入输出格式
输入格式:
第一行两个数n和Q分别表示树的点数和幽香操作的个数,其中点从1到n标号。 接下来n-1行,每行三个正整数a,b,c,表示a和b之间有一条边权为c的边。 接下来Q行,每行两个数u,e,表示幽香在点u上放了e单位个军队(如果e<0,就相当于是幽香在u上减少了|e|单位个军队,说白了就是du←du+e)。数据保证任何时刻每个点上的军队数量都是非负的。
输出格式:
对于幽香的每个操作,输出操作完成以后,每天的最小花费,也即如果幽香选择最优的补给点进行补给时的花费。
输入输出样例
10 5 1 2 1 2 3 1 2 4 1 1 5 1 2 6 1 2 7 1 5 8 1 7 9 1 1 10 1 3 1 2 1 8 1 3 1 4 1
0 1 4 5 6
说明
对于所有数据,1<=c<=1000, 0<=|e|<=1000, n<=10^5, Q<=10^5 非常神奇的是,对于所有数据,这棵树上的点的度数都不超过20,且N,Q>=1
我们具体来分析一下这道题目我们要维护什么
题目要求使$\sum d_v*dis(u,v)$最小,其中$d_v$为$v$点的点权,$dis(u,v)$为原树中$u,v$两点的距离。题目要求就是求带权重心。假设我们当前已经选定了点$v$为答案,那么考虑它的一个子节点$w$,如果把补给站从点$v$转移到$w$,那么$w$的所有子树内的点到补给站的距离少了$dis(v,w)$,而其他所有点到补给站的距离多了$dis(v,w)$。我们假设$sum_v[v]$为$v$的子树内的点权和,那么答案总共的变化量是$$dis(u,v)*(sum_v[v]-sum_v[w]-sum_v[w])$$
不难发现,当$sum_v[w]*2>sum_v[v]$的时候,答案的变化量是小于零的,也就是说代价减小,可以变得更优。而且,满足这样条件的点$w$最多只有一个
那么我们可以每一次选定一个点,然后看看往他的哪个子树走更优,如果没有说明他自己就已经是最优的了。这样不断下去肯定能找到答案。
但是由于原图可能是一条链,要怎么做才能保证复杂度呢?我们选择在点分树上走,每一次都跳到它下一层的重心,这样可以保证层数最多只有$O(log n)$
然后考虑如何维护答案。不难发现,对于点分树上一个点$v$,它的子树就是在点分治时它被选为重心时的那棵树。考虑点分树上的一对父子$u,v$,我们设$sum_a[v]$表示$v$的子树内的所有点到他的代价之和,$sum_b[v]$为$v$的子树内的所有点到$v$点父亲(也就是点$u$)的距离之和,$sum_v[v]$还是表示子树的点权之和。那么我们设答案已经选定为点$w$,并且已经把$v$这一整棵子树上所有点到点$w$的距离之和计算完毕,那么考虑要加上$v$在点分树上的父亲$u$,要计算的答案只有$u$的不包含$v$的子树,答案是$sum_a[v]+sum_a[u]-sum_b[v]+sum_v[u]*dis(u,v)$。于是只要在点分树上不断找父亲并合并,就可以知道答案了
然后我们只要能在修改时维护好这三个数组就可以了
至于修改时如何维护呢?我们修改一个点之后,然后不断在点分树上往父节点跳,每一次只会对它的祖先节点的这些值产生影响,一个一个修改即可
ps:还有个小细节,因为我们判断是否更优要在原树上走,然后计算答案要在点分树里走,所以对于每一个节点不仅要记录它的父亲,还要记录它往下能走哪几条边,在原树的边判断是否更优,然后往点分树上走来保证计算答案的复杂度
然后又新学会了一招,用$RMQ O(1)$查询$LCA$(只会倍增和树剖的我瑟瑟发抖),总时间复杂度$O(nlog^2n)$

1 //minamoto 2 #include<cstdio> 3 #include<iostream> 4 #include<cstring> 5 #define ll long long 6 #define N 100005 7 #define inf 0x3f3f3f3f 8 #define rint register int 9 using namespace std; 10 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 11 char buf[1<<21],*p1=buf,*p2=buf; 12 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} 13 inline int read(){ 14 #define num ch-'0' 15 char ch;bool flag=0;int res; 16 while(!isdigit(ch=getc())) 17 (ch=='-')&&(flag=true); 18 for(res=num;isdigit(ch=getc());res=res*10+num); 19 (flag)&&(res=-res); 20 #undef num 21 return res; 22 } 23 char sr[1<<21],z[20];int C=-1,Z; 24 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 25 inline void print(ll x){ 26 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 27 while(z[++Z]=x%10+48,x/=10); 28 while(sr[++C]=z[Z],--Z);sr[++C]='\n'; 29 } 30 struct G{ 31 int head[N],Next[N<<1],edge[N<<1],ver[N<<1],tot; 32 G(){tot=0;memset(head,0,sizeof(head));} 33 inline void add(int u,int v,int e){ 34 ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; 35 } 36 }T1,T2; 37 int n,q,st[N<<1][18],logn[N<<1],bin[25],tp; 38 ll sum,ans,d[N],dis1[N],dis2[N],sumv[N]; 39 int dfn[N],num; 40 void dfs1(int u,int fa){ 41 st[dfn[u]=++num][0]=d[u]; 42 for(int i=T1.head[u];i;i=T1.Next[i]){ 43 int v=T1.ver[i]; 44 if(v==fa) continue; 45 d[v]=d[u]+T1.edge[i],dfs1(v,u),st[++num][0]=d[u]; 46 } 47 } 48 inline ll LCA(int a,int b){ 49 if(dfn[a]>dfn[b]) a^=b^=a^=b; 50 int k=logn[dfn[b]-dfn[a]+1]; 51 return min(st[dfn[a]][k],st[dfn[b]-bin[k]+1][k])<<1; 52 } 53 inline ll dis(int a,int b){return d[a]+d[b]-LCA(a,b);} 54 int sz[N],son[N],size,rt,fa[N];bool vis[N]; 55 void dfs2(int u,int fa){ 56 sz[u]=1,son[u]=0; 57 for(int i=T1.head[u];i;i=T1.Next[i]){ 58 int v=T1.ver[i]; 59 if(vis[v]||v==fa) continue; 60 dfs2(v,u),sz[u]+=sz[v],cmax(son[u],sz[v]); 61 } 62 cmax(son[u],size-sz[u]); 63 if(son[u]<son[rt]) rt=u; 64 } 65 void dfs3(int u){ 66 vis[u]=true; 67 for(int i=T1.head[u];i;i=T1.Next[i]){ 68 int v=T1.ver[i]; 69 if(vis[v]) continue; 70 rt=0,size=sz[v],son[0]=n+1; 71 dfs2(v,0),T2.add(u,rt,v),fa[rt]=u,dfs3(rt); 72 } 73 } 74 inline void update(int u,int val){ 75 sumv[u]+=val; 76 for(int p=u;fa[p];p=fa[p]){ 77 ll dist=dis(fa[p],u)*val; 78 dis1[fa[p]]+=dist; 79 dis2[p]+=dist; 80 sumv[fa[p]]+=val; 81 } 82 } 83 inline ll calc(int u){ 84 ll ans=dis1[u]; 85 for(int p=u;fa[p];p=fa[p]){ 86 ll dist=dis(fa[p],u); 87 ans+=dis1[fa[p]]-dis2[p]; 88 ans+=dist*(sumv[fa[p]]-sumv[p]); 89 } 90 return ans; 91 } 92 ll query(int u){ 93 ll ans=calc(u); 94 for(int i=T2.head[u];i;i=T2.Next[i]){ 95 ll tmp=calc(T2.edge[i]); 96 if(tmp<ans) return query(T2.ver[i]); 97 } 98 return ans; 99 } 100 void init(){ 101 n=read(),q=read(); 102 bin[0]=1,logn[0]=-1; 103 for(rint i=1;i<=20;++i) bin[i]=bin[i-1]<<1; 104 while(bin[tp+1]<=(n<<1)) ++tp; 105 for(rint i=1;i<=(n<<1);++i) logn[i]=logn[i>>1]+1; 106 for(rint i=1;i<n;++i){ 107 rint u=read(),v=read(),e=read(); 108 T1.add(u,v,e),T1.add(v,u,e); 109 } 110 dfs1(1,0),rt=0,son[0]=n+1,size=n,dfs2(1,0); 111 for(rint j=1;j<=tp;++j) 112 for(rint i=1;i+bin[j]-1<=(n<<1);++i) 113 st[i][j]=min(st[i][j-1],st[i+bin[j-1]][j-1]); 114 } 115 int main(){ 116 init(); 117 int LastOrder=rt;dfs3(rt); 118 while(q--){ 119 int x=read(),y=read();update(x,y); 120 print(query(LastOrder)); 121 } 122 Ot(); 123 return 0; 124 }
BZOJ4012 [HNOI2015]开店 (动态点分治)
Description
风见幽香有一个好朋友叫八云紫,她们经常一起看星星看月亮从诗词歌赋谈到
Input
第一行三个用空格分开的数 n、Q和A,表示树的大小、开店的方案个数和妖
Output
对于每个方案,输出一行表示方便值。
Sample Input
0 0 7 2 1 4 7 7 7 9
1 2 270
2 3 217
1 4 326
2 5 361
4 6 116
3 7 38
1 8 800
6 9 210
7 10 278
8 9 8
2 8 0
9 3 1
8 0 8
4 2 7
9 7 3
4 7 0
2 2 7
3 2 1
2 3 4
Sample Output
957
7161
9466
3232
5223
1879
1669
1282
0
HINT
满足 n<=150000,Q<=200000。对于所有数据,满足 A<=10^9
我们考虑对于每一个点分树上的点维护什么。我们记录三个值,$sz_0$表示子树内的点数之和,$sz_1$表示子树内所有点到其的距离之和,$sz_2$表示子树内所有点到其父亲的距离之和。那么考虑我们在跳点分树的时候要如何维护答案呢?很明显$sz_1[u]+\sum sz_1[fa]-sz_2[p]+(sz_0[fa]-sz_0[p])*dist(fa,u)$就是在点分树上与$u$的$LCA$是$fa$的所有点的距离之和,其中$fa$为$p$的父亲,$p$为从$u$不断跳父亲直到根,那么只要不断枚举$fa$,并不断往上跳并维护答案就可以了。
然而上面只是为了方便理解,因为具体的计算不是这样的。我们对于$u$点内部的贡献可以直接计算,然后考虑往上跳。在上述的式子中如果一个点$p$有$fa$,那么答案就要减去$sz_0[p]*dist(fa,u)+sz_2[p]$,如果一个点不是$u$那么答案就要加上$sz_0[p]+dist(p,u)$,然后每一个点都要加上自己的$sz_1$。按这个规律在跳点分树的时候不断加就好了
然后考虑怎么在$[l,r]$之内,很明显可以搞一个差分,把每一个节点在点分树上的子树内的所有年龄的距离之和加起来,再做前缀和,那么在年龄$[l,r]$的人数就是$[1,r]-[1,l-1]$(因为实际上存储时不可能按年龄,所以可以在每一个点开一个vector然后排序一下即可)

1 //minamoto 2 #include<cstdio> 3 #include<iostream> 4 #include<cstring> 5 #include<vector> 6 #include<algorithm> 7 #define ll long long 8 #define N 150005 9 using namespace std; 10 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 11 char buf[1<<21],*p1=buf,*p2=buf; 12 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} 13 inline int read(){ 14 #define num ch-'0' 15 char ch;bool flag=0;int res; 16 while(!isdigit(ch=getc())) 17 (ch=='-')&&(flag=true); 18 for(res=num;isdigit(ch=getc());res=res*10+num); 19 (flag)&&(res=-res); 20 #undef num 21 return res; 22 } 23 char sr[1<<21],z[20];int C=-1,Z; 24 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 25 inline void print(ll x){ 26 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 27 while(z[++Z]=x%10+48,x/=10); 28 while(sr[++C]=z[Z],--Z);sr[++C]='\n'; 29 } 30 int head[N],Next[N<<1],ver[N<<1],edge[N<<1]; 31 int n,tot,val[N],q,maxn; 32 int st[N<<1][19],d[N],dfn[N],num,bin[25],tp,logn[N<<1]; 33 inline void add(int u,int v,int e){ 34 ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; 35 ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e; 36 } 37 inline void ST(){ 38 for(int j=1;j<=tp;++j) 39 for(int i=1;i+bin[j]-1<=(n<<1);++i) 40 st[i][j]=min(st[i][j-1],st[i+bin[j-1]][j-1]); 41 } 42 void dfs1(int u,int fa){ 43 st[dfn[u]=++num][0]=d[u]; 44 for(int i=head[u];i;i=Next[i]){ 45 int v=ver[i]; 46 if(v==fa) continue; 47 d[v]=d[u]+edge[i],dfs1(v,u),st[++num][0]=d[u]; 48 } 49 } 50 int fa[N],sz[N],son[N],size,rt;bool vis[N]; 51 void dfs2(int u,int fa){ 52 sz[u]=1,son[u]=0; 53 for(int i=head[u];i;i=Next[i]){ 54 int v=ver[i]; 55 if(vis[v]||v==fa) continue; 56 dfs2(v,u),sz[u]+=sz[v],cmax(son[u],sz[v]); 57 } 58 cmax(son[u],size-sz[u]); 59 if(son[u]<son[rt]) rt=u; 60 } 61 inline ll dis(int a,int b){ 62 if(dfn[a]>dfn[b]) a^=b^=a^=b; 63 int k=logn[dfn[b]-dfn[a]+1]; 64 return d[a]+d[b]-(min(st[dfn[a]][k],st[dfn[b]-bin[k]+1][k])<<1); 65 } 66 struct node{ 67 int val;ll sz[3]; 68 node(int a=0,ll b=0,ll c=0,ll d=0){val=a,sz[0]=b,sz[1]=c,sz[2]=d;} 69 inline bool operator <(const node &b)const 70 {return val<b.val;} 71 }; 72 vector<node> sta[N]; 73 void dfs3(int u,int f,int rt){ 74 sta[rt].push_back(node(val[u],1,dis(u,rt),fa[rt]?dis(u,fa[rt]):0)); 75 for(int i=head[u];i;i=Next[i]){ 76 int v=ver[i]; 77 if(v==f||vis[v]) continue; 78 dfs3(v,u,rt); 79 } 80 } 81 void dfs4(int u){ 82 vis[u]=true; 83 dfs3(u,0,u);sta[u].push_back(node(-1,0,0,0)); 84 sort(sta[u].begin(),sta[u].end()); 85 for(int i=0,j=sta[u].size();i<j-1;++i) 86 sta[u][i+1].sz[0]+=sta[u][i].sz[0], 87 sta[u][i+1].sz[1]+=sta[u][i].sz[1], 88 sta[u][i+1].sz[2]+=sta[u][i].sz[2]; 89 for(int i=head[u];i;i=Next[i]){ 90 int v=ver[i]; 91 if(vis[v]) continue; 92 rt=0,size=sz[v]; 93 dfs2(v,0),fa[rt]=u,dfs4(rt); 94 } 95 } 96 inline node query(int id,int l,int r){ 97 if(id==0) return node(); 98 vector<node>::iterator it1=upper_bound(sta[id].begin(),sta[id].end(),node(r,0,0,0));--it1; 99 vector<node>::iterator it2=upper_bound(sta[id].begin(),sta[id].end(),node(l-1,0,0,0));--it2; 100 return node(0,it1->sz[0]-it2->sz[0],it1->sz[1]-it2->sz[1],it1->sz[2]-it2->sz[2]); 101 } 102 inline ll calc(int u,int l,int r){ 103 ll res=0; 104 for(int p=u;p;p=fa[p]){ 105 node a=query(p,l,r); 106 res+=a.sz[1]; 107 if(p!=u) res+=a.sz[0]*dis(p,u); 108 if(fa[p]) res-=a.sz[2]+a.sz[0]*dis(fa[p],u); 109 } 110 return res; 111 } 112 int main(){ 113 ll ans=0; 114 n=read(),q=read(),maxn=read(); 115 bin[0]=1,logn[0]=-1; 116 for(int i=1;i<=20;++i) bin[i]=bin[i-1]<<1; 117 while(bin[tp+1]<=(n<<1)) ++tp; 118 for(int i=1;i<=(n<<1);++i) logn[i]=logn[i>>1]+1; 119 for(int i=1;i<=n;++i) val[i]=read(); 120 for(int i=1;i<n;++i){ 121 int u=read(),v=read(),e=read(); 122 add(u,v,e); 123 } 124 dfs1(1,0),ST(); 125 rt=0,son[0]=n+1,size=n,dfs2(1,0); 126 dfs4(rt); 127 while(q--){ 128 int a=read(),b=read(),c=read(); 129 b=(b+ans)%maxn,c=(c+ans)%maxn; 130 if(b>c) b^=c^=b^=c; 131 print(ans=calc(a,b,c)); 132 } 133 Ot(); 134 return 0; 135 }
emm……最后再来两个大boss吧(我已经想(抄)到了一种很棒的解法可惜这里写不下)
说真的抄代码其实很累的
洛谷P3676 小清新数据结构题--------->蒟蒻的题解
bzoj3435 [Wc2014]紫荆花之恋(权限)(非权限)---------------->蒟蒻的题解
那么就到这里吧……感谢观看……累死我了……


