bzoj4199: [Noi2015]品酒大会(后缀数组)
题目描述
一年一度的“幻影阁夏日品酒大会”隆重开幕了。大会包含品尝和趣味挑战 两个环节,分别向优胜者颁发“首席品酒家”和“首席猎手”两个奖项,吸引了众多品酒师参加。
在大会的晚餐上,调酒师 Rainbow 调制了 n 杯鸡尾酒。这 n 杯鸡尾酒排成一行,其中第 n 杯酒 (1 ≤ i ≤ n) 被贴上了一个标签si,每个标签都是 26 个小写 英文字母之一。设 str(l, r)表示第 l 杯酒到第 r 杯酒的 r − l + 1 个标签顺次连接构成的字符串。若 str(p, po) = str(q, qo),其中 1 ≤ p ≤ po ≤ n, 1 ≤ q ≤ qo ≤ n, p ≠ q, po − p + 1 = qo − q + 1 = r ,则称第 p 杯酒与第 q 杯酒是“ r 相似” 的。当然两杯“ r 相似”(r > 1)的酒同时也是“ 1 相似”、“ 2 相似”、……、“ (r − 1) 相似”的。特别地,对于任意的 1 ≤ p , q ≤ n , p ≠ q ,第 p 杯酒和第 q 杯酒都 是“ 0 相似”的。
在品尝环节上,品酒师 Freda 轻松地评定了每一杯酒的美味度,凭借其专业的水准和经验成功夺取了“首席品酒家”的称号,其中第 i 杯酒 (1 ≤ i ≤ n) 的 美味度为 ai 。现在 Rainbow 公布了挑战环节的问题:本次大会调制的鸡尾酒有一个特点,如果把第 p 杯酒与第 q 杯酒调兑在一起,将得到一杯美味度为 ap*aq 的 酒。现在请各位品酒师分别对于 r = 0,1,2, ⋯ , n − 1 ,统计出有多少种方法可以 选出 2 杯“ r 相似”的酒,并回答选择 2 杯“ r 相似”的酒调兑可以得到的美味度的最大值。
输入输出格式
输入格式:
第 1 行包含 1 个正整数 n ,表示鸡尾酒的杯数。
第 2 行包含一个长度为 n 的字符串 S,其中第 i 个字符表示第 i 杯酒的标签。
第 3 行包含 n 个整数,相邻整数之间用单个空格隔开,其中第 i 个整数表示第 i 杯酒的美味度 ai 。
输出格式:
包括 n 行。第 i 行输出 2 个整数,中间用单个空格隔开。第 1 个整 数表示选出两杯“ (i − 1) 相似”的酒的方案数,第 2 个整数表示选出两杯 “ (i − 1) 相似”的酒调兑可以得到的最大美味度。若不存在两杯“ (i − 1) 相似” 的酒,这两个数均为 0 。
输入输出样例
10 ponoiiipoi 2 1 4 7 4 8 3 6 4 7
45 56 10 56 3 32 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12 abaabaabaaba 1 -2 3 -4 5 -6 7 -8 9 -10 11 -12
66 120 34 120 15 55 12 40 9 27 7 16 5 7 3 -4 2 -4 1 -4 0 0 0 0
说明
【样例说明 1】
用二元组 (p, q) 表示第 p 杯酒与第 q 杯酒。
0 相似:所有 45 对二元组都是 0 相似的,美味度最大的是 8 × 7 = 56 。
1 相似: (1,8) (2,4) (2,9) (4,9) (5,6) (5,7) (5,10) (6,7) (6,10) (7,10) ,最大的 8 × 7 = 56 。
2 相似: (1,8) (4,9) (5,6) ,最大的 4 × 8 = 32 。
没有 3,4,5, ⋯ ,9 相似的两杯酒,故均输出 0 。
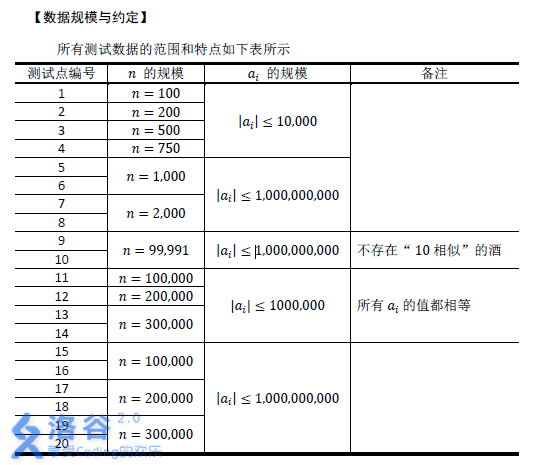
【时限1s,内存512M】
题解
我果然还是太弱……学了这么久后缀系列竟然连这么一道裸题都看不出来……
考虑一下,如果两杯酒是$r$相似的,那么他们肯定也是$[0,r-1]$相似的,所以大的可以对小的产生贡献
于是就跑一遍SA,求出height数组,然后把height从大到小排个序,每次取出height一样的合并就是了
考虑怎么合并,可以用并查集实现,两个集合合并之后方案数$sum[x]+=size[x]*size[y]$(因为两个集合中所有元素都是$r$相似的,而且集合中的两两匹配已经考虑过了,所以只要加上两个集合之间互相匹配的就是了),然后再用$mx[x]*mx[y]$和$mn[x]*mn[y]$更新一下$ans[x]$就可以了(记录最小是因为负负得正)
据说这题还有SAM的做法,因为做的时候只要考虑两串的最长相似,然后答案做一下前缀和。而一对串的最长相似就是两个后缀的lcp,直接把原串翻转SAM转后缀树,然后dfs一遍即可(明明这么裸我居然没有看出来啊岂可修)
1 //minamoto 2 #include<cstdio> 3 #include<algorithm> 4 #include<iostream> 5 #include<cstring> 6 #define ll long long 7 using namespace std; 8 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 9 char buf[1<<21],*p1=buf,*p2=buf; 10 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} 11 template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,1:0;} 12 inline int read(){ 13 #define num ch-'0' 14 char ch;bool flag=0;int res; 15 while(!isdigit(ch=getc())) 16 (ch=='-')&&(flag=true); 17 for(res=num;isdigit(ch=getc());res=res*10+num); 18 (flag)&&(res=-res); 19 #undef num 20 return res; 21 } 22 char sr[1<<21],z[30];int C=-1,Z; 23 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 24 inline void print(ll x,char ch){ 25 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 26 while(z[++Z]=x%10+48,x/=10); 27 while(sr[++C]=z[Z],--Z);sr[++C]=ch; 28 } 29 const int N=300005; 30 int s[N],y[N],x[N],c[N],sa[N],rk[N],h[N]; 31 int n,m; 32 int fa[N],sz[N];ll ans[N],sum[N],mx[N],mn[N],val[N]; 33 struct node{ 34 int h,x,y; 35 node(){} 36 node(int h,int x,int y):h(h),x(x),y(y){} 37 inline bool operator <(const node &b)const 38 {return h>b.h;} 39 }g[N]; 40 int ff(int x){return fa[x]==x?x:fa[x]=ff(fa[x]);} 41 void unite(int x,int y){ 42 fa[y]=x,sz[x]+=sz[y]; 43 cmax(mx[x],mx[y]),cmin(mn[x],mn[y]); 44 } 45 void get_sa(){ 46 m=26; 47 for(int i=1;i<=n;i++) ++c[x[i]=s[i]]; 48 for(int i=2;i<=m;i++) c[i]+=c[i-1]; 49 for(int i=n;i>=1;i--) sa[c[x[i]]--]=i; 50 for(int k=1;k<=n;k<<=1){ 51 int num=0; 52 for(int i=n-k+1;i<=n;i++) y[++num]=i; 53 for(int i=1;i<=n;i++) if(sa[i]>k) y[++num]=sa[i]-k; 54 for(int i=1;i<=m;i++) c[i]=0; 55 for(int i=1;i<=n;i++) ++c[x[i]]; 56 for(int i=2;i<=m;i++) c[i]+=c[i-1]; 57 for(int i=n;i>=1;i--) sa[c[x[y[i]]]--]=y[i],y[i]=0; 58 swap(x,y); 59 x[sa[1]]=1; 60 num=1; 61 for(int i=2;i<=n;i++) 62 x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num; 63 if(num==n) break; 64 m=num; 65 } 66 } 67 void get_h(){ 68 int k=0; 69 for(int i=1;i<=n;i++) rk[sa[i]]=i; 70 for(int i=1;i<=n;i++){ 71 if(rk[i]==1) continue; 72 if(k) k--; 73 int j=sa[rk[i]-1]; 74 while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k]) k++; 75 h[rk[i]]=k; 76 } 77 } 78 int main(){ 79 n=read(); 80 for(int i=1;i<=n;++i) s[i]=getc()-'a'+1; 81 for(int i=1;i<=n;++i) val[i]=read(); 82 get_sa(),get_h(); 83 for(int i=1;i<=n;++i){ 84 fa[i]=i,sz[i]=1; 85 mx[rk[i]]=mn[rk[i]]=val[i]; 86 } 87 for(int i=2;i<=n;++i) g[i-1]=node(h[i],i,i-1); 88 sort(g+1,g+n); 89 memset(sum,128,sizeof(sum)); 90 for(int i=g[1].h,j=1;i>=0;--i){ 91 ans[i]=ans[i+1],sum[i]=sum[i+1]; 92 for(;j<n&&g[j].h==i;++j){ 93 int x=ff(g[j].x),y=ff(g[j].y); 94 cmax(sum[i],mn[x]*mn[y]); 95 cmax(sum[i],mx[x]*mx[y]); 96 ans[i]+=1ll*sz[x]*sz[y]; 97 unite(x,y); 98 } 99 } 100 for(int i=0;i<n;++i){ 101 print(ans[i],' '); 102 print(ans[i]==0?0:sum[i],'\n'); 103 } 104 Ot(); 105 return 0; 106 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号