P2146 [NOI2015]软件包管理器

题目描述

Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。Debian/Ubuntu使用的apt-get，Fedora/CentOS使用的yum，以及OSX下可用的homebrew都是优秀的软件包管理器。

你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包A依赖软件包B，那么安装软件包A以前，必须先安装软件包B。同时，如果想要卸载软件包B，则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除0号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而0号软件包不依赖任何一个软件包。依赖关系不存在环（若有m(m≥2)个软件包A1,A2,A3,⋯,Am，其中A1依赖A2，A2依赖A3，A3依赖A4，……，A[m-1]依赖Am，而Am依赖A1，则称这m个软件包的依赖关系构成环），当然也不会有一个软件包依赖自己。

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为0。

输入输出格式

输入格式：

 

从文件manager.in中读入数据。

输入文件的第1行包含1个整数n，表示软件包的总数。软件包从0开始编号。

随后一行包含n−1个整数，相邻整数之间用单个空格隔开，分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。

接下来一行包含1个整数q，表示询问的总数。之后q行，每行1个询问。询问分为两种：

install x：表示安装软件包x

uninstall x：表示卸载软件包x

你需要维护每个软件包的安装状态，一开始所有的软件包都处于未安装状态。

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

 

输出格式：

 

输出到文件manager.out中。

输出文件包括q行。

输出文件的第i行输出1个整数，为第i步操作中改变安装状态的软件包数。

 

输入输出样例

输入样例#1： 复制 
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0
输出样例#1： 复制 
3
1
3
2
3
输入样例#2： 复制 
10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9
输出样例#2： 复制 
1
3
2
1
3
1
1
1
0
1

说明

【样例说明 1】

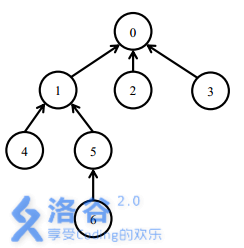
一开始所有的软件包都处于未安装状态。

安装5号软件包，需要安装0,1,5三个软件包。

之后安装6号软件包，只需要安装6号软件包。此时安装了0,1,5,6四个软件包。

卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。

之后安装4号软件包，需要安装1,4两个软件包。此时0,1,4处在安装状态。最后，卸载0号软件包会卸载所有的软件包。`

【数据范围】

【时限1s，内存512M】

 

题解

嗯……树链剖分的题目……

有点懵逼……看了看大佬们的题解才知道树剖还有这么多讲究……

首先，我们可以将所有的软件看作一棵树，初始时都是-1

对于安装操作，相当于将它到根节点的路径上的点全都变为1

对于卸载操作，相当于将它的子树全都变为0

然后只要输出每次操作前后整棵树权值的变化量即可

卸载操作的话……直接在dfs序后的线段树上区间覆盖

安装操作的话……在树剖树上向上走，然后不断更新路径即可

  1 //minamoto
  2 #include<iostream>
  3 #include<cstdio>
  4 #include<algorithm>
  5 using namespace std;
  6 typedef long long LL;
  7 const int N=200005;
  8 struct SegmentTree{
  9     int l,r;
 10     LL sum,add;
 11     #define l(x) tree[x].l
 12     #define r(x) tree[x].r
 13     #define sum(x) tree[x].sum
 14     #define add(x) tree[x].add
 15 } tree[N*4];
 16 int n,m,a[N],top_,num;
 17 int size[N],son[N],fa[N],dep[N],top[N],cnt[N],rnk[N];
 18 int ver[N*2],Next[N*2],head[N];char s[20];
 19 int read()
 20 {
 21     int x=0,f=1;
 22     char ch=getchar();
 23     for (; !isdigit(ch); ch=getchar()) if(ch=='-') f=-1;
 24     for (; isdigit(ch); ch=getchar()) x=x*10+ch-'0';
 25     return x*f;
 26 }
 27 void add_(int x,int y){
 28     ver[++top_]=y,Next[top_]=head[x],head[x]=top_;
 29 }
 30 void dfs(int x){
 31     size[x]=1,dep[x]=dep[fa[x]]+1;
 32     for(int i=head[x];i;i=Next[i]){
 33         int y=ver[i];
 34         if(y!=fa[x]){
 35             fa[y]=x;
 36             dfs(y);
 37             size[x]+=size[y];
 38             if(!son[x]||size[y]>size[son[x]]){
 39                 son[x]=y;
 40             }
 41         }
 42     }
 43 }
 44 void dfs_(int x){
 45     if(!top[x]) top[x]=x;
 46     cnt[x]=++num,rnk[num]=x;
 47     if(son[x]) top[son[x]]=top[x],dfs_(son[x]);
 48     for(int i=head[x];i;i=Next[i]){
 49         int y=ver[i];
 50         if(y!=fa[x]&&y!=son[x]){
 51             dfs_(y);
 52         }
 53     }
 54 }
 55 void build(int p,int l,int r)
 56 {
 57     l(p)=l,r(p)=r;
 58     if(l==r) {sum(p)=0,add(p)=-1;return;}
 59     int mid=(l+r)>>1;
 60     build(p<<1,l,mid);
 61     build((p<<1)|1,mid+1,r);
 62 }
 63 void spread(int p)
 64 {
 65     if(~add(p))
 66     {
 67         int lc=p<<1,rc=(p<<1)+1;
 68         sum(lc)=add(p)*(r(lc)-l(lc)+1),sum(lc);
 69         sum(rc)=add(p)*(r(rc)-l(rc)+1),sum(rc);
 70         add(lc)=add(p);
 71         add(rc)=add(p);
 72         add(p)=-1;
 73     }
 74 }
 75 void update(int p,int l,int r,int d)
 76 {
 77     if(l<=l(p)&&r>=r(p))
 78     {
 79         sum(p)=1ll*d*(r(p)-l(p)+1);
 80         add(p)=d;
 81         return;
 82     }
 83     spread(p);
 84     int mid=(l(p)+r(p))>>1;
 85     if(l<=mid) update(p<<1,l,r,d);
 86     if(r>mid) update((p<<1)+1,l,r,d);
 87     sum(p)=sum(p<<1)+sum((p<<1)+1);
 88 }
 89 void change(int u,int v,int val){
 90     while(top[u]!=top[v]){
 91         if(dep[top[u]]<dep[top[v]]) swap(u,v);
 92         update(1,cnt[top[u]],cnt[u],val);
 93         u=fa[top[u]];
 94     }
 95     if(dep[u]>dep[v]) swap(u,v);
 96     update(1,cnt[u],cnt[v],val);
 97     return;
 98 }
 99 int main()
100 {
101     //freopen("testdata.in","r",stdin);
102     n=read();
103     for(int i=2;i<=n;++i){
104         int x=read();++x;
105         add_(x,i);
106     }
107     m=read();
108     dfs(1),dfs_(1);build(1,1,n);
109     while(m--){
110         scanf("%s",s);
111         int x=read();++x;
112         int t1=sum(1);
113         if(s[0]=='i'){
114             change(1,x,1);
115             int t2=sum(1);
116             printf("%d\n",abs(t1-t2));
117         }
118         else{
119             update(1,cnt[x],cnt[x]+size[x]-1,0);
120             int t2=sum(1);
121             printf("%d\n",abs(t1-t2));
122         }
123     }
124     return 0;
125 }

 

posted @ 2018-07-18 13:44  bztMinamoto  阅读(339)  评论(0)  编辑  收藏  举报
Live2D