注意事项以及一些奇怪的姿势

本文用于总结各种奇怪的姿势，仅供个人学习，有的地方可能直接引用原文，并无冒犯之意

计数

0.做题想到思路之后先去证明！实在不会证明去找反例！找不出反例再看几遍题目！确定没问题了再去敲代码！

1.主席树空间尽量往大了开

2.LCT的splay维护链信息下传加法标记的时候要维护size，否则加法标记下传会出问题

3.LCT的isroot判断的是该点是否是splay中的根！不是原树的根！

4.splay的pop之后记得pushup

5.点分时递归找根的时候这样写\(size=sz[v]>sz[rt]?totsz-sz[rt]:sz[v],rt=0;\)

upd：然而一般的写法并不会退化所以实际上不用这样写

6.看到棋盘先黑白染色冷静一下

7.最少需要多少可以转化为最多能拿走多少再转化为最大流

8.混合图求欧拉回路->这里

9.最小割树->这里

10.手动模拟队列的时候队列大小要开节点被访问的次数而不是节点个数！！

11.整数概率公式$$E(x)=\sum_{i=1}^\infty P(x\geq i)$$
即\(x\)取值的期望等于它大于等于某数的概率之和

证明如下：$$E(x)=\sum_{i=1}^\infty i*P(i)$$
这是期望的定义

\[E(x)=\sum_{i=1}^\infty i*(P(x\geq i)-P(x\geq i+1)) \]

然后把上式一项一项展开之后，合并同类项可得$$E(x)=\sum_{i=1}^\infty P(x\geq i)$$

12.考虑一个下标从\(0\)开始的数列，这个数列的每个数均为\(1\)。 我们对这个数列做\(k\)阶前缀和，得到的数列第\(i\)项的值为\(C_{k+i}^k\)

如果对一个区间\([l,r]\)每一个数字加上\(1\)，相当于它的一阶差分的更改。因为差分和前缀和互为逆运算，设\(cha[i][j]\)表示\(i\)阶差分的第\(j\)位，那么上面的区间加可以看做是\(cha[1][l]++\)，\(ch[i][r+1]--\)（1可以看做是\(C_{0+i-l}^0\)）。同理，推广到区间\([l,r]\)中的数\(a_i\)加上\(C_{k+i-l}^{k}\)可以看做是它的\(cha[k+1][l]++\)，\(cha[k+1][r+1]--\)。然而这样还不够，我们之前假设是区间全部为\(1\)，才能\(k\)阶前缀和后有如上的性质。而现在进行了这两个操作，一阶前缀和后只有\([l,r]\)区间全都是\(1\)，也就是说再继续前缀和下去也只有这个区间会满足上面的性质，也就满足我们要求的区间加。然而\(r+1\)及后面会加上一些不该加的东西。于是我们还得对\(1\leq i\leq k\)阶差分的第\(r+1\)项做一下修改，也就是减去该阶差分数组的前缀和，即\(C_{k-i+1+r-l}^{k-i+1}\)（为什么是这个手推一下，很难表述啊……）

代码长这样（dec是减）

while(m--){
    int l=read(),r=read(),k=read();
    cha[k+1][l]++,cha[k+1][r+1]--;
    for(int i=k;i;--i)
    cha[i][r+1]=dec(cha[i][r+1],C[k-i+1+r-l][k-i+1]);
}

13.\(i\)个节点的带标号连通图的个数（枚举\(1\)所在的连通块中有多少点，容斥减去不合法的）$$f_i=2^{{\dbinom{i}{2}}-\sum_{j=1}}2^{\dbinom{i-j}{2}}\dbinom{i-1}{j-1} f_j$$

14.不要什么时候都用线段树常数太大了而且空间太炸，多想想树状数组，哪怕是需要查询\([i-k,i+k]\)之类的也可以预处理之后离散化，如果\(k\)是询问时才给的可以每一次读进来在lower_bound或upper_bound

15.手打队列的时候空间开大开大开大，实在不行的话用STL或者让头尾指针对\(n\)取模

16.题目要求取模的话，加减乘除都要取模

17.如果有的题目不保证正解与树有关，而口胡出的做法需要dfs整棵树，还是手动模拟深搜比较好，防止爆栈

18.对于可以化成\(b-a|k\)的约数条件，考虑化成\(b\equiv a\pmod{k}\)

19.\(n!\)中质因子\(2\)的个数等于\(n\)减去\(n\)的二进制表示中\(1\)的个数。

20.枚举子集的时候如果直接暴力枚举是\(O(m*3^n)\)的（一共有\(m\)个数且每个数二进制有\(n\)位），按一下两种看不懂的写法是\(O(m*2^n)\)

for (int i=1;i<=m;i++) {
    scanf("%d",&x);
    s[x]++;
}
for (int i=0;i<n;i++)
	for (int j=1;j<=(1<<n)-1;j++) if (j&(1<<i)) s[j^(1<<i)]+=s[j];

for(rint i=1;i<=m;++i)x=read(),++cnt[x];
for (int len = 2; len <= (1 << n); len <<= 1) {
    for (int i = 0; i <= lim; i += len)
    for (int j = i, k = i + len / 2; k < i + len; j++, k++)
        cnt[j] += cnt[k];
}

21.判断一个数的因子（可以用多次也可以不用）加起来能否等于另一个数\(n\)，首先只有质因子有用。质因子只有一个直接判断，两个用exgcd解，三个的话，那么把最小质因子\(x\)提出来，剩下的数肯定能构成形如\(T\equiv n\pmod{x}\)的情况，只要构成的\(T\)小于等于\(n\)肯定能加上一些\(x\)使其成立。所以只要在模意义下，将每个点\(u\)向\(u+c_i\)连边（\(c_i\)为除最小质因子之外的其他质因子），跑最短路，那么从\(0\)到\(n\ mod\ x\)的最短路就是所求的\(T\)，判断它是否小于等于\(n\)即可

22.统计某一个数二进制最低位的\(1\)在第几位

for(rint i=1;i<lim;++i)lst[i]=(i&1)?1:lst[i>>1]+1;

23.一种奇特的BFS方法，适用于点特别少的时候，其中\(s\)表示需要达到的状态，\(Q\)中的每一位表示该位是否在队列中，\(vis\)表示该位是否被访问，\(lst\)表示该状态下二进制最低的\(1\)的位置（即上面那个），\(ct\)表示该状态的代价。如果能够从一开始不断枚举到最终状态，说明该方案可行

int vis=0,Q=s&-s;
while(Q){
    int c=lst[Q];
    vis|=1<<c-1,Q^=1<<c-1,Q|=f[c]&s&~vis;
}
if(vis==s&&ct[ans]>ct[s])ans=s;

24.若三点在某一条经过原点的直线上的投影中心对称，设三点坐标分别为\((x_a,y_a),(x_b,y_b),(x_c,y_c)\)，则\((y_a+y_c-2*y_b,-x_a-x_c+2*x_b)\)为该直线上一点，其中\(B\)点的投影为对称中心

25.有关树的路径的问题可以考虑两端的取值范围，用dfs序转化为矩阵覆盖的问题

26.写读优的时候最后不要忘了返回resf，不要忘记f，否则会导致读入负数挂掉

27.有向图中的最小平均权值回路->这里

28.求\(1\)到\(n\)的异或和\(O(1)\)

inline int calc(R int n){int t=n&3;return t&1?(t/2^1):(t/2^n);}

29.\(Min-Max\)容斥

设\(max(S)\)为集合\(S\)中最大值，\(min(S)\)为集合中最小值，\(|S|\)为集合的元素个数，则有

\[max(S)=\sum_{T\subseteq S}(-1)^{|T|+1}min(T) \]

\[min(S)=\sum_{T\subseteq S}(-1)^{|T|+1}max(T) \]

以第一个等式为例，假设集合中元素两两不同（有相同的可以通过加上\(eps\)扰动，反正最大最小值不会变），设元素\(b\)的排名为\(k\)，那么\(min(T)=b\)当且仅当\(T\)为后面的\(n-k\)个元素的集合的子集加上\(b\)，那么后面那些元素的子集共有\(2^{n-k}\)个，其中集合大小为奇数和为偶数的都有\(2^{n-k-1}\)个，两两相消就都变成\(0\)了。只有在\(b\)的排名为\(n\)的时候不满足，此时这个集合\(T=\{b\}\)，\(min(T)\)自然等于\(b\)。于是我们发现整个集合里只有最大的元素会有贡献，其他全都没了，证毕

第二个等式同理

\(Min-Max\)容斥对期望同样成立

具体应用

拓展\(Min-Max\)容斥$$\max_k(S)=\sum_{T\subseteq S}(-1)^{|T|-k}{|T|-1\choose k-1}min(T)$$

\[\min_k(S)=\sum_{T\subseteq S}(-1)^{|T|-k}{|T|-1\choose k-1}max(T) \]

以第一个等式为例，对于第\(p\)大元素\(v\)，如果\(p<k\)贡献为\(0\)，那么\(min(T)=v\)当且仅当集合是由\(v\)以及后面的元素的子集加上\(v\)，贡献为$$\sum_{i=1}^p{p-1\choose i-1}(-1)^{i-k}{i-1\choose k-1}$$
即枚举集合大小，然后加上贡献，其中\({p-1\choose i-1}\)表示大小为\(i\)且\(min(T)=v\)的集合个数

上式可以改写成$$\sum_{i=1}^p(-1)$$

原式可以看成从\(p-1\)个数中选\(i-1\)个再从\(i-1\)个中选\(k-1\)个，改成从\(p-1\)个数中选\(k-1\)在从剩下的数中选剩下的\((i-1)-(k-1)=i-k\)个

\({p-1\choose k-1}\)是常数，提到前面之后剩下的就是个裸的容斥系数了，当\(p=k\)时为\(1\)，否则为\(0\)

证毕

30.离散随机变量的几何分布

如果有一个离散型随机变量\(X\)，满足$$P(X==k)=(1-p)^{k-1}p$$
其中\(p\)是一个常数，那么称\(X\)服从以\(p\)为参数的几何分布

然后关于服从几何分布的随机变量的期望$$E(X)=\sum i*P(x==i)$$

\[E(X)=p\sum i*(1-p)^{i-1} \]

这是一个等比*等差数列的求和公式，运用高中数学姿势可得$$E(x)=p\frac{1}{p^2}=\frac{1}{p}$$

31.循环卷积->这里（\(k\)进制下不进位加法）

32.一个可重集合\(S\)中任取一个子集\(T\)，记其中所有元素的异或和为\(x\)，那么\(x\)取到所有能取到的值的概率是相等的

证：设\(n=|S|\)，\(S\)中线性基的大小为\(Base\)，我们考虑在那些不在线性基中的元素取数，共有\(2^{n-Base}\)中取法，对于每一种取法取到的值\(x\)，线性基中有唯一对应的取法取到\(x\)，所以在线性基中取数使得所有元素异或和为\(0\)的方案数是\(2^{n-Base}\)

\(x\)能取到的每一个值\(v\)都可以被线性基中的元素唯一表示，记为\(L\)，所有使异或和\(x\)为\(v\)的集合一定是形如\(L\)异或上元素异或和为\(0\)的集合\(T\)，所以个数取到每个\(v\)的方案数都是\(2^{n-Base}\)，所以概率相等

33.对于树的直径（考虑点数），如果直径为奇数，所有直径有同一个中点，如果直径为偶数，所有直径有同一条最中间的边

34.\(n\)个节点的完全图的生成树个数为\(n^{n-2}\)->证明

35.斐波那契数列的前缀和\(S(n)=f(n+2)-1\)

证明：当\(n=1\)时显然成立

假设当\(1~n-1\)时成立，那么\(S(n)=S(n-1)+f(n)=f(n+1)+f(n)-1=f(n+2)-1\)

综上，原命题成立

36.当\(p\)为质数时，有$$\prod_{i=1}^p(x+i)\equiv x(x^{p-1}-1)\pmod{p}$$

证：对于\(\prod_{i=1}^p(x+i)\)，在模\(p\)意义下有且仅有\(p\)个根\(0,1,2,...,p-1\)

根据费马小定理，对于\(0<x<p\)，\(x^{p-1}\equiv 1\pmod{p}\)恒成立，所以\(x(x^{p-1}-1)\)也有且仅有\(p\)个根\(0,1,2,...,p-1\)

因为\(Z_p[x]\)是唯一分解整环（咱也不知道这是个啥），所以这两个多项式相等

37.任意长度的\(DFT\)

考虑\(DFT\)，有

\[\begin{align*} y_k &= \sum_{i = 0}^{n - 1} a_i \omega_n^{ki}\\ &= \sum_{i = 0}^{n - 1} a_i \omega_{2n}^{-(k - i)^2 +k^2+i^2}\\ &= \omega_{2n}^{k^2} \sum_{i = 0}^{n - 1} a_i \omega_{2n}^{i^2} \times \omega_{2n}^{-(k - i)^2} \end{align*} \]

和式是个卷积，可以用\(FFT\)计算

简单来说就是可以用卷积来计算\(DFT\)

38.合并两棵树时，设\(a,b\)为\(A\)的直径的两个端点，\(c,d\)为\(B\)的直径的两个端点，那么新的树的直径一定是\(ab,ac,ad,bc,bd,cd\)中的一个

证明：新树的直径一定是原树的直径或一条经过\((u,v)\)的链（其中\((u,v)\)为新加的边），这条经过\((u,v)\)的链肯定是\(A\)中离\(u\)最远的点到\(u+(u,v)+v\)到\(B\)中离\(v\)最远的点，感性理解一下易知，其中前者必为\(a\)或\(b\)，后者必为\(c\)或\(d\)

39.特征值与特征向量

如果等式$$(\lambda E-A)v=0$$

则称\(\lambda\)为矩阵\(A\)的特征值，\(v\)为矩阵\(A\)的特征向量

以及两个结论：

①.如果大小为\(n\)的矩阵\(A\)满秩（即行列式不为\(0\)），则\(A\)有\(n\)组线性无关的特征向量

②.如果\(Det(\lambda E-A)=0\)，则存在\(v\)使等式成立，否则不存在

40.\(Cayley-Hamilton\)定理

当\(A\)满秩时，下列等式恒成立

\[\prod_{k}(\lambda_{k} E-A)=0 \]

其中\(\lambda_{k}\)表示\(A\)的第\(k\)个特征值

直接证明它为\(0\)很难，我们可以考虑证明任意向量乘上它为\(0\)

因为它的\(n\)组特征向量线性无关，所以任意向量都可以被这\(n\)组特征向量表示，那么只要证明任意特征向量乘上它为\(0\)即可

首先，我们证明这玩意儿满足交换律

\[(aE-A)(bE-A)=abE^2-aEA-bEA+A^2=(bE-A)(aE-A) \]

那么就可以把里面的给提出来

\[v_i\prod_{k}(\lambda_{k} E-A)=v_i(\lambda_{i} E-A)\prod_{k\neq i}(\lambda_{k} E-A)=0 \]

41.\(\prod_{k}(\lambda_{k} E-A)\)和\(f(\lambda)=Det(\lambda E-A)\)，把它们看做两个多项式的话，那么这两个多项式的系数相等

大概可以这么理解，方程$$\prod_{k}(\lambda_{k} E-A)=0$$

的解为\(A\)的\(n\)个特征值，所以这个多项式的系数可以写成\(f(x)=\prod_{k}(\lambda_i-x)\)，后面那个多项式的解也是\(A\)的\(n\)个特征值，所以系数也可以写成这样的形式。所以这两个多项式系数相等

42.$$\ln(1-x^{i)=-\sum_{j=1}}\frac{x^{ij}}{j}$$

证明如下

\[\ln F(x)=G(x)\\\frac{F'(x)}{F(x)}=G'(x)\\\frac{-ix^{i-1}}{1-x^i}=G'(x)\\-\sum_{j=0}^{\infty} ix^{i-1+ij}=G'(x)\\-\sum_{j=0}^{\infty}\frac{ix^{i+ij}}{i+ij}=G(x)\\-\sum_{j=1}^{\infty}\frac{x^{ij}}{j}=G(x) \]

43.$$\sum_{i=1}^n i[\gcd(i,n)=1]={\varphi(n)\times n+[n=1]\over 2}$$

\(n=1\)时显然成立

若\(n\neq 1\)，因为\([(n,i)=1]\Longrightarrow [(n-i,i)=1]\)

\[\begin{align} 2\sum_{i=1}^n i[\gcd(i,n)=1] &=\sum_{i=1}^n i[\gcd(i,n)=1]+\sum_{i=1}^n i[\gcd(n,n-i)=1]\\ &=\sum_{i=1}^n i[\gcd(i,n)=1]+\sum_{i=1}^n n-i[\gcd(n,i)=1]\\ &=\sum_{i=1}^n n[\gcd(i,n)=1]\\ &=n\varphi(n)\\ \end{align} \]

44.$$\sigma_1(ij)=\sum_{p|i}\sum_{q|j}[\gcd(p,q)=1]{pj\over q}$$

其中\(\sigma_1(i)\)表示\(i\)的因子的和

我们分别考虑每一个质因子\(d\)，设\(i\)中\(d\)的次数为\(a\)，\(j\)中\(d\)的次数为\(b\)，如果\(d\mid p\)且\(d\nmid q\)，那么\({pj\over q}\)可以取遍\(d^{b+1}\)到\(d^{b+a}\)之间的所有次数，否则如果\(d\nmid p\)且\(d\mid q\)，\({pj\over q}\)可以取遍\(d^{0}\)到\(d^b\)之间的所有次数，综上\(d\)可以取遍所有的次数，所以所有的数都会被统计到

45.\(\begin{align} \sum_{i=1}^n i\left\lfloor\frac n i\right\rfloor=\sum_{i=1}^n\sigma_1(i) \end{align}\)

因为\(\left\lfloor\frac n d\right\rfloor\)的实际意义就是\(\le n\)的所有数中是\(i\)的倍数的数的个数（可用于\(\sigma_1\)的快速求和）

46.指数型生成函数形如

\[G(x) = a_0 + a_1x + a_2\frac{x^2}{2!} + a_3\frac{x^3}{3!} + a_4\frac{x^4}{4!} + \dots = \sum\limits_{i = 0}^{\infty} a_i\frac{x^i}{i!} \]

对于两个指数型生成函数\(F(x)\)和\(G(x)\)的卷积有

\[\begin{aligned} F(x) \centerdot G(x) &= (\sum\limits_{i = 0}^{\infty} a_i \frac{x^i}{i!})(\sum\limits_{i = 0}^{\infty} b_i \frac{x^i}{i!}) \\ &= \sum\limits_{n = 0}^{\infty} (\sum\limits_{i = 0}^{\infty} \frac{a_ix^i}{i!} \centerdot \frac{b_{n - i}x^{n - i}}{(n - i)!})x^n \\ &= \sum\limits_{n = 0}^{\infty} (\sum\limits_{i = 0}^{\infty} {n \choose i} a_i b_{n - i}) \frac{x^n}{n!} \end{aligned} \]

上面的式子意思就是，如果\(F(x)\)中\(x^i\)的系数表示从\(F\)的所有物品中选择\(i\)个的排列个数，\(G(x)\)同理，那么\(F\times G\)中的第\(x^i\)项的系数就代表从\(F\)和\(G\)中共选\(i\)个物品的排列数（考虑里面，假设\(F\)选了\(i\)个物品，\(G\)选了\(j\)个物品，那么一个新的排列就是把它们合起来，并保证\(i\)个物品之间的相对顺序不变，\(j\)个物品的相对顺序也不变，方案数就是\({i+j\choose i}\)）

47.设满足性质\(A\)的集合为\(S_A\)，集合有标号，并设\(S_B\)为若干个\(S_A\)构成的一个大集合

设\(a_i\)为大小为\(i\)的\(S_A\)的个数，\(b_i\)为大小为\(i\)的\(S_B\)的个数，那么\(S_A\)和\(S_B\)的指数型生成函数分别为

\[A(x)=\sum_{i=0}^\infty a_i{x^i\over i!} \]

\[B(x)=\sum_{i=0}^\infty b_i{x^i\over i!} \]

考虑\(S_B\)由多少个\(S_A\)构成，又因为选出的\(S_A\)是无序的所以要乘上一个\(i!\)，于是有

\[B(x)=\sum_i\frac{A^i(x)}{i!}=e^{A(x)} \]

比方说\(A(x)\)代表所有的无向连通图的生成函数，\(B(x)\)表示所有的无向图的生成函数，那么有\(B(x)=e^{A(x)}\)

48.假设一个边集\(T\)对应的森林有k个联通块，第 \(i\) 个联通块的大小是 \(a_{i}\) ，那么我们断言

\[C(T)=N^{k-2}\prod_{i=1}^{k}a_{i} \]

其中 \(C(T)\) 表示含有\(T\)这个集合的边的树的个数

证明的话我们采取矩阵树定理+手玩行列式的方法来证明它

当然我们需要先构造出一张图来，具体点来讲我们将第i个联通块当中的点缩成一个点i，然后我们在点i和点j之间连接 \(a_{i}a_{j}\) 条重边，这样形成的图的生成树个数就是边集包含 \(T\) 的树的个数,(应该很好理解这样做为什么是对的，自己画画图就明白了)

那么这样建出来图的基尔霍夫矩阵应该长这样

\[\left[\begin{matrix}a_{1}(n-a_{1}) & -a_{1}a_{2} & \cdots& -a_{1}a_{k} \\ -a_{2}a_{1} & a_{2}(n-a_{2}) & \cdots & -a_{2}a_{k} \\ \vdots & \vdots & \ddots & \vdots \\ -a_{k}a_{1} & -a_{k}a_{2} & \cdots & a_{k}(n-a_{k}) \end{matrix} \right] \]

然后我们删去一行一列之后会变成这样

\[\left[\begin{matrix}a_{1}(n-a_{1}) & -a_{1}a_{2} & \cdots& -a_{1}a_{k-1} \\ -a_{2}a_{1} & a_{2}(n-a_{2}) & \cdots & -a_{2}a_{k-1} \\ \vdots & \vdots & \ddots & \vdots \\ -a_{k-1}a_{1} & -a_{k-1}a_{2} & \cdots & a_{k-1}(n-a_{k-1}) \end{matrix} \right] \]

接下来我们将第 \(i\) 行除去 \(a_{i}\) 这样最终的行列式需要乘上一个 \(\prod_{i=1}^{k-1}a_{i}\) ，矩阵会变成这样

\[\left[\begin{matrix}(n-a_{1}) & -a_{2} & \cdots& -a_{k-1} \\ -a_{1} & (n-a_{2}) & \cdots & -a_{k-1} \\ \vdots & \vdots & \ddots & \vdots \\ -a_{1} & -a_{2} & \cdots & (n-a_{k-1}) \end{matrix} \right] \]

然后我们将第2列到第k-1列加到第1列上，会得到

\[\left[\begin{matrix}a_{k} & -a_{2} & \cdots& -a_{k-1} \\ a_{k} & (n-a_{2}) & \cdots & -a_{k-1} \\ \vdots & \vdots & \ddots & \vdots \\ a_{k} & -a_{2} & \cdots & (n-a_{k-1}) \end{matrix} \right] \]

接下来我们用第1行去减其他的行，会得到

\[\left[\begin{matrix}a_{k} & -a_{2} & \cdots& -a_{k-1} \\ 0 & n & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & n \end{matrix} \right] \]

这样矩阵就被我们削成了一个上三角阵，它的行列式是 \(n^{k-2}a_{k}\) 乘上 \(\prod_{i=1}^{k-1}a_{i}\) 就是

\[n^{k-2}\prod_{i=1}^{k}a_{i} \]

这样我们就证明了我们的式子是正确的

49.$$x^n-yn=(x-y)(x^{n-1}+xy+x^{n-3}y2+...+y^{n-1})$$

证明：当\(x=y\)时等式为\(0\)，故原式含有因式\((x-y)\)

\[x^n-y^n=(x^n-x^{n-1}y)+(x^{n-1}y-x^{n-2}y^2)+...+(xy^{n-1}-y^n) \]

然后每一项都提出一个公因式\((x-y)\)即可得证

50.$${1\over k}\sum_{i=0}^{k-1}\omega_k=[k|n]$$

直接等比数列求和公式带进去就行了

51.Simpson公式$$\int_a^bf(x)dx\approx\frac{(b-a)(f(a)+f(b)+4f(\frac{a+b}{2}))}{6}$$

对于原函数，我们找一个二次函数来拟合它

\[\begin{aligned} \int_a^bf(x)dx &\approx\int_a^bAx^2+Bx+C\\ &=\frac{A}{3}(b^3-a^3)+\frac{B}{2}(b^2-a^2)+C(a-b)\\ &=\frac{(b-a)}{6}(2A(b^2+ab+a^2)+3B(b+a)+6C)\\ &=\frac{(b-a)}{6}(2Ab^2+2Aab+2Aa^2+3Bb+3Ba+6C)\\ &=\frac{(b-a)}{6}(Aa^2+Ba+C+Ab^2+Bb+C+4A(\frac{a+b}{2})^2+4B(\frac{a+b}{2})+4C)\\ &=\frac{(b-a)}{6}(f(a)+f(b)+4f(\frac{a+b}{2}))\\ \end{aligned} \]

52.欧拉公式$$V-E+F=2$$

\(V:vertex\)顶点

\(E:edge\)边

\(F:flat\)面

对所有维度的所有多边形都成立

53.圆的反演

反演中心为\(O\)，常数为\(k\)，若经过\(O\)的直线经过\(P,P'\)，且\(OP\times OP'=k\)，则称\(P,P'\)关于\(O\)互为反演，其中\(O\)为反演中心，\(k\)为反演幂

以及一些性质（这里\(O\)指反演中心）

1.一根过\(O\)的直线的反形是本身

2.一根不过\(O\)的直线的反形是一个过\(O\)的圆

3.一个过\(O\)的圆的反形是一根不过\(O\)的直线

4.一个不过\(O\)的圆的反形是一个和该圆关于\(O\)位似的圆

5.反演不改变相切关系

可以大概这么解释：两个不同颜色的三角形相似，易证直线\(CD\)关于\(E\)的反演是一个圆

关于\(4\)大概是长这个样子

54.无向图三元环计数

我们把每一条边重定向，设它连接的两个点的度数分别为\(deg_u\)和\(deg_v\)，那么把这条边定为从度数大的连向度数小的，如果度数相同按标号大小。这样显然可以建出一个有向无环图

所以怎么找环呢

我们枚举点\(u\)，并枚举它的所有出边，把出边指向的点\(v\)标记上\(u\)。然后再枚举一边出边，并对每个\(v\)也枚举出边，如果\(v\)的出边指向的点\(w\)上的标记是\(u\)那么说明找到了一个三元环

显然，每个三元环都会被统计恰好一次

接下来的问题是复杂度，我们要证明它的上界是\(O(m\sqrt{m})\)

1.\(\forall v,out_v\leq \sqrt{m}\)，每一次枚举\(v\)的出边的复杂度不会超过\(O(\sqrt{m})\)，所以这一部分复杂度不会超过\(O(m\sqrt{m})\)

2.\(\forall v,out_v\geq \sqrt{m}\)，因为在这种情况下必有\(deg_u\geq deg_v\)，所以所有这样的\(u\)不会超过\(O(\sqrt{m})\)个，每一个\(out_v\)的贡献最多是\(\sqrt{m}out_v\)，由于\(\sum out_v=O(m)\)，所以这一部分的复杂度也不会超过\(O(m\sqrt{m})\)

55.这是一个可以\(O(n)\)求出\(n\)个数逆元的方案

先把所有的数做一个前缀积，记为\(s_i\)

然后我们用快速幂求出\(s_n\)的逆元，记为\(sv_n\)

因为\(sv_n\)是\(a_1\)到\(a_n\)的逆元，我们把它乘上\(a_n\)，就得到了\(sv_{n-1}\)

同理可得\(sv_{1,...,n-2}\)

那么\(a_i\)的逆元就可以用\(sv_i\times s_{i-1}\)来表示了

顺便还有\(O(s)\)预处理，\(O(1)\)求快速幂的办法（\(s=\sqrt{P}\)）（给定\(x\)的情况下）

预处理出\(x^0,x^1,...,x^s\)，以及\(x^0,x^s,x^{2s},...\)，然后就可以\(O(1)\)询问了

55.环的染色方案数

我们现在要对一个环进行染色，要求两两颜色不同，设点的个数为\(n\)，颜色个数为\(c\)，求方案数

设\(f_i\)表示\(i\)个点的染色方案数。我们可以钦定一个开头，设为\(1\)，并顺时针一次记为\(2,3,...,n\)

如果\(1\)号点和\(n-1\)号点颜色不同，那么方案数为\(f_{n-1}，\)\(n\)号点可以选的方案数就是\((c-2)\)

如果\(1\)号点和\(n-1\)号点颜色相同，那么方案数为\(f_{n-2}\)，即等价于\(n-2\)个点的环再插一个进去，此时\(n\)号点的颜色方案数为\(c-1\)

所以我们可以求得递推公式

\[f_n=(c-2)f_{n-1}+(c-1)f_{n-2} \]

初值为\(f_0=1,f_1=c\)

根据数列的特征方程（因为我数学课老师讲这个的时候我快睡着了所以我也不是很清楚所以具体百度），我们可以求得\(f_n\)的通项公式为

\[f_n=(c-1)^n+(-1)^n(c-1) \]

顺带一提，如果需要如果强制环的两个端点相同的话，方案显然就是\(f_{n-1}\)

56.\(O(n^2)\)多项式\(Ln\)和多项式\(Exp\)

其实这里是可以\(O(n\log n)\)搞的然而代码实在太长而，且这里数据范围够小所以我们可以\(O(n^2)\)做，如果您耐心够好而且对自己的多项式码力有自信完全可以跳过这一节

经过\(shadowice\)巨巨一个下午的调教我终于会了

对于多项式\(Ln\)，我们需要暴力的就是它求逆的过程，即我们需要暴力计算一个形如

\[F(x)={P(x)\over Q(x)} \]

的柿子

根据\(Ln\)的使用条件，得有\([x^0]Q(x)=1\)

我们令\(T(x)=Q(x)-1\)，则\(Q(x)=T(x)+1\)，即

\[F(x)={P(x)\over T(x)+1} \]

\[F(x)(T(x)+1)=P(x) \]

\[F(x)=P(x)-F(x)T(x) \]

因为有\([x^0]T(x)=0\)，所以我们就可以直接暴力卷积把\(F(x)\)给一项一项卷出来了，卷完之后积分一下就可以求出\(Ln\)了

然后是多项式\(Exp\)，即要求

\[F(z)=e^{G(z)} \]

\[F'(z)=G'(z)F(z) \]

没了

多项式\(Ln\)

int main(){
//	freopen("testdata.in","r",stdin);
	n=read();
	fp(i,0,n-1)A[i]=read();
	--A[0];
	inv[0]=inv[1]=1;fp(i,2,n)inv[i]=mul(P-P/i,inv[P%i]);
	fp(i,0,n-1){
		B[i]=0;
		fp(j,0,i)B[i]=add(B[i],mul(A[i-j],B[j]));
		B[i]=dec(mul(A[i+1],i+1),B[i]);
	}
	fd(i,n-1,1)B[i]=mul(B[i-1],inv[i]);B[0]=0;
	fp(i,0,n-1)print(B[i]);
	return Ot(),0;
}

多项式\(Exp\)

int main(){
//	freopen("testdata.in","r",stdin);
	n=read();
	fp(i,0,n-1)A[i]=read();
	fp(i,1,n-1)A[i-1]=mul(A[i],i);A[n-1]=0;
	inv[0]=inv[1]=1;fp(i,2,n)inv[i]=mul(P-P/i,inv[P%i]);
	B[0]=1;
	fp(i,0,n-1){
		res=0;
		fp(j,0,i)res=add(res,mul(A[i-j],B[j]));
		B[i+1]=mul(res,inv[i+1]);
	}
	fp(i,0,n-1)print(B[i]);
	return Ot(),0;
}

57.对于线性规划

\[Ax+By+C<0 \]

不论\(A,B,C\)符号如何，这个线性规划对应的半平面永远是\((-B,A)\)（也就是说设这个向量为\(x\)，\(Ax+By+C=0\)上任意一点为\(p\)，那么\(p,p+x\)这两个点确定的直线的左边就是对应的半平面）

58.对\(1+p+p^2+...+p^{k-1}\)求和，可以直接用等比数列求和公式代入计算\({1-p^k\over1-p}\)，复杂度\(O(\log P)\)（求逆元）

或者把长为\(k\)的数列拆成\(\log k\)段计算，复杂度\(O(\log k)\)

int calc(R int x,R int y){
	R int res=1,d=1;
	for(--y;y;y>>=1,d=add(mul(d,x),d),x=mul(x,x))(y&1)?res=add(mul(res,x),d):0;
	return res;
}

59.计算几何中的平面图转对偶图->这里

60.混合积

对于三个三维向量\(a,b,c\)，定义它们的混合积为\((a\times b)\cdot c\)，其中$\times \(表示叉乘，\)\cdot\(表示点乘，记为\)[a\ b\ c]$

关于它的几何意义的话……图片来自网络

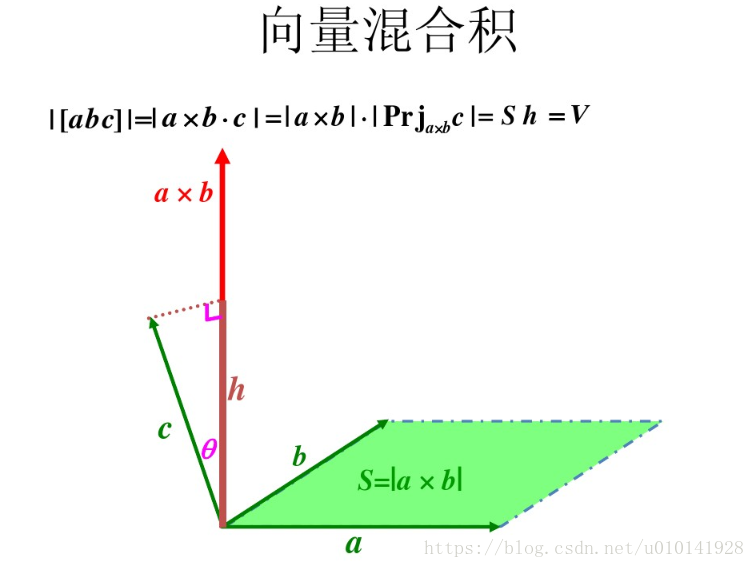
其中\(Prj_{a\times b}c\)代表的是\(c\)这个向量在\(a\times b\)这个向量上的投影

那么显然我们最后得到的是以这三个向量为三条临边的一个六面体的体积

61.四面体体积

假设四面体的四个顶点分别为\(A,B,C,D\)，并设三个向量\(a=B-A,b=C-A,c=D-A\)，那么这个正四面体的体积就是\({1\over 6}[a\ b\ c]\)

这个应该比较显然吧……看上面那幅图，四面体的体积是以\(ab\)这个平行四边形为底，\(c\)为顶点的棱锥的一半，而棱锥的体积是棱柱的\({1\over 3}\)，所以四面体体积就是六面体的\({1\over 6}\)了

62.凸多面体的重心

我们先来考虑一下凸多边形的重心好了……

对于三角形，它的重心就是它所有坐标的平均值

那么对于凸多边形，我们把它三角剖分了，记第\(i\)块的重心为\(a_i\)，面积为\(m_i\)，那么凸多边形的重心就是

\[{\sum_{i=1}^na_i\times m_i\over \sum_{i=1}^nm_i} \]

那么凸多面体也差不多了，我们把它给四面体剖分了，然后也差不多按上面的算就好了

关于四面体剖分，具体的说我们在多面体中随便选一个点，比方说是\(p_1\)，然后把每一个面给三角剖分，那么三角形就和选定的点构成了一个四面体。设\(v_i\)表示第\(i\)个四面体的体积，\(a_i\)表示重心，则最终多面体的重心为

\[{\sum_{i=1}^na_i\times v_i\over \sum_{i=1}^nv_i} \]

62.二面角

这玩意儿班里数学课正在上然而我正在停课

简单来说就是两个平面的夹角

我们假设现在有\(a,b,c\)三个向量，要求\(ab\)这个平面和\(ac\)这个平面的二面角

那么求出\(ab\)和\(ac\)的法向量（法向量可以直接用叉积算），两个法向量之间的夹角就是二面角了，法向量之间的夹角直接用点积除以长度计算

可以画个图来理解。我们俯视的话，即要求二面角\(\angle 1\)，那么显然两个法向量的夹角\(\angle 2=\angle 1\)

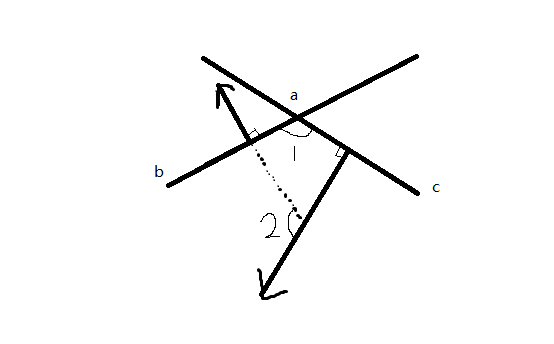
63.设直线\(y=kx+b\)，点\((x,y)\)，则点到直线的距离为

\[{|kx-y+b|\over \sqrt{k^2+1}} \]

64.求到\(n\)个点的距离的平方和最小的直线->这里

求到\(n\)条直线距离的平方和最小的点->这里

65.曼哈顿距离和切比雪夫距离

对于两个点\((x_i,y_i)\)和\(x_j,y_j\)，我们定义它们之间的曼哈顿距离为

\[|x_i-x_j|+|y_i-y_j| \]

定义它们的切比雪夫距离为

\[\max(|x_i-x_j|,|y_i-y_j|) \]

有如下转换：

将原坐标为\((x,y)\)的点转化为\((x+y,x-y)\)之后，原坐标系中的曼哈顿距离等于新坐标系中的切比雪夫距离

将原坐标为\((x,y)\)的点转化为\(({x+y\over 2},{x-y\over 2})\)之后，原坐标系中的切比雪夫距离等于新坐标系中的曼哈顿距离

这里只证后一个，因为前一个就是它反过来

证明：

首先我们有一个结论

\[\max\left({|a+b|,|a-b|}\right)=|a|+|b| \]

分类讨论就能证明了

那么两个点重构之后的坐标为\(({x_i+y_i\over 2},{x_i-y_i\over 2}),({x_j+y_j\over 2},{x_j-y_j\over 2})\)，设为\((x_i',y_i'),(x_j',y_j')\)，那么现在它们之间的距离为

\[\begin{aligned} Ans &=\max(|x_i-x_j|,|y_i-y_j|)\\ &=\max(|(x_i'+y_i')-(x_j'+y_j')|,|(x_i'-y_i')-(x_j'-y_j')|)\\ &=\max(|(x_i'-x_j')+(y_i'-y_j')|,|(x_i'-x_j')-(y_i'-y_j')|)\\ &=|x_i'-x_j'|+|y_i'-y_j'| \end{aligned} \]

没了

66.笛卡尔定理

我们定义一个圆的曲率为\(k=\pm {1\over r}\)，其中\(r\)是圆的半径

若在平面上有两两相切，且六个切点互不相同的四个圆，设其曲率分别为\(k1,k2,k3,k4\)（若该圆和其它所有圆都外切，则其曲率取正，否则曲率取负），则有

\[(k1+k2+k3+k4)^2=2(k1^2+k2^2+k3^2+k4^2) \]

类似的，若是空间中有两两相切且切点互不相同的五个球体，则有

\[(k1+k2+k3+k4+k5)^2=3(k1^2+k2^2+k3^2+k4^2+k5^2) \]

67.巴什博奕

\(Nim\)游戏的改版，我们现在每次最多只能取走\(k\)个石子，那么\(SG\)函数很容易写出来

\[SG(x)=mex_{i=1}^{\min(x,k)}SG(x-i) \]

有\(SG(0)=0\),用归纳法易知\(SG(x)=x\bmod (k+1)\)

68.阶梯博弈

有\(n\)级台阶，从\(0\)级开始数到\(n\)级。每级上都有一定的石子。每次可以把一个阶梯的石子往下移，\(0\)级阶梯的不能移，不能操作者输。

这里有一个结论，我们只需要考虑所有奇数层，该游戏就等价于\(Nim\)游戏

为啥嘞？

首先偶数层是不会有任何影响的，因为如果你移动偶数层若干个石子到奇数层，那么对手一定可以通过移动把你移的石子移到下一个偶数层，相当于这些石子仍然在偶数层。如果移动奇数层的石子，我们就默认它消失了

69.设\(i\)和\(j\)在\([1,n]\)上随机取值的离散型随机变量，则\(\max(i,j)\)的期望是\(O({2\over 3}n)\)，\(|i-j|\)的期望是\(O({1\over 3}n)\)

关于前面那个，我们枚举最大值，然后计算有多少对的最大值为它

\[\begin{aligned} E(\max(i,j)) &={1\over n^2}\sum_{k=1}^nk\times (2k-1)\\ &={1\over n^2}\left(2\sum_{k=1}^nk^2-\sum_{k=1}^nk\right)\\ &={1\over n^2}\left({2n(n+1)(2n+1)\over 6}-{3n(n+1)\over 6}\right)\\ &={1\over n^2}\left({4n^3+3n^2-n\over 6}\right)\\ &=O({2\over 3}n)\\ \end{aligned} \]

关于后面这个，记\(s(i)=\sum\limits_{k=1}^ik\)，我们枚举第一个位置选在哪儿

\[\begin{aligned} E(|i-j|) &={1\over n^2}\left(\sum_{k=1}^ns(k-1)+s(n-k)\right)\\ &={1\over n^2}\left(2\sum_{k=1}^{n-1}s(k)\right)\\ &={1\over n^2}\left(\sum_{k=1}^{n-1}k(k-1)\right)\\ &={1\over n^2}\left(\sum_{k=1}^{n-1}k^2-k\right)\\ \end{aligned} \]

具体不算下去了（我也算不动……），看一下前面那个大概可以猜出它是\(O({1\over 3}n)\)了

70.平面上随机\(n\)个点，凸包上的期望点数是\(O(n^{1\over 3})\)（据说这好像已经是个结论了？）

71.在\([0,1]\)上插入\(n-1\)个点使其分成\(n\)条线段，最短线段的长度期望是\({1\over n^2}\)

72.暴力多项式取模

我们要计算\(A(x)\bmod{B(x)}\)，首先有\(B(x)\equiv 0\pmod{B(x)}\)，那么设\(B\)的最高次项次数为\(m\)，就有\(x^m\equiv -{1\over b_m}\sum_{i=0}^{m-1}b_ix^i\pmod{B(x)}\)，把\(A(x)\)中所有次数大于\(m\)的项都这样暴力分解就行了

poly Mod(poly A,poly B){
	int n=A.size(),m=B.size();
	fd(i,n-1,m-1)if(A[i]){
		int t=mul(P-A[i],ksm(B[m-1],P-2));
		fp(j,0,m-1)A[i-j]=(A[i-j]+1ll*t*B[m-1-j])%P;
	}
	while(!A.empty()&&!A.back())A.pop_back();
	return A;
}