treap

1.是什么？

treap是一种二叉平衡树，其中每个点通常包含两个值（z1,z2）z1满足平衡树性质也就是根据z1的得到的中序遍历是升序的，z2满足最小堆的性质，也就是父亲的z2<儿子的z2

且z1为题目所给的值，z2为随机产生（保证期望深度<=log(n)）

2.treap支持哪些操作？

（1）插入

当插入一个数z(对应z1)的时候,我们从根开始走，设目前在点k

如果x[k].z1==z,那么我们就将次数的记录++即可

如果x[k].z1<z,那么这个数应该放在右子树

如果x[k].z1>z,则放在左子树

当我们发现这个点是空的，那么就可以把这个数放在这里，x[k].z1=z,并且，随机赋值一个z2

然后我们思考，既然是随机赋值，那就有可能不满足最小堆的性质

那么我们就要通过旋转使其满足

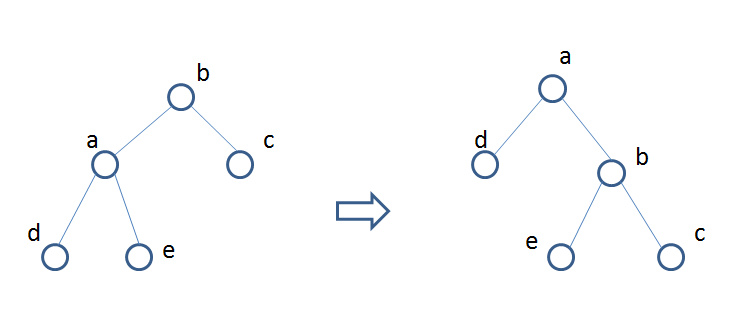
如下图我们观察这种变换不会改变中序遍历

但是却改变了a,b两个点的关系

也就是说假设原本a，b不满足最小堆的性质，那么这样旋转后就满足了

所以只需要这样旋转就可以了

具体其实是b和b的一个儿子a不满足最小堆的性质，此时我们就把e变为b的左儿子，b变为a的右儿子

如果a是b的右儿子的话所进行的操作则与上述镜面对称

（2）删除

删除的时候要记得,找到需要删除的点之后如果这个点既有左儿子也有右儿子那么就要把它的位置通过旋转向下调整到只有左儿子或者只有右儿子或者都没有再删除

（3）求一个数的排名，排名为x的数，前驱，后继

这个根据二叉树的性质就可以求出。

模板题：https://www.luogu.org/problemnew/show/P3369

#include<cstdio>
#include<cstdlib>
const int N=1e5+5;
struct X{
    int z1,z2,s[2],sz,sl;
}x[N];
int s,ans;
void xz(int& k,int p){
    int t=x[k].s[p];
    x[k].s[p]=x[t].s[p^1];
    x[t].s[p^1]=k;
    x[t].sz=x[k].sz;
    x[k].sz=x[x[k].s[0]].sz+x[x[k].s[1]].sz+x[k].sl;
    k=t;
}
void cr(int& k,int z){
    if(!k){
        k=++s;
        x[k].z1=z;
        x[k].z2=rand();
        x[k].sz=x[k].sl=1;
        return;
    }
    ++x[k].sz;
    if(x[k].z1==z) ++x[k].sl;
    else{
        int p=z>x[k].z1;
        cr(x[k].s[p],z);
        if(x[x[k].s[p]].z2<x[k].z2) xz(k,p); 
    }
}
void de(int &k,int z){
    if(x[k].z1==z){
        if(x[k].sl>1) --x[k].sl,--x[k].sz;
        else if(x[k].s[0]&&x[k].s[1]){
            int p=x[x[k].s[1]].z2<x[x[k].s[0]].z2;
            xz(k,p);--x[k].sz;
            de(x[k].s[p^1],z);
        }
        else x[k].sl=x[k].sz=0,k=x[k].s[0]+x[k].s[1];
    }
    else --x[k].sz,de(x[k].s[z>x[k].z1],z);
}
int ask3(int k,int z){
    if(!k) return 0;
    int t=x[x[k].s[0]].sz;
    if(x[k].z1==z) return t;
    else if(x[k].z1>z) return ask3(x[k].s[0],z);
    else return t+x[k].sl+ask3(x[k].s[1],z);
}
int ask4(int k,int z){
    int t=x[x[k].s[0]].sz;
    if(t+x[k].sl<z) return ask4(x[k].s[1],z-t-x[k].sl);
    else if(t>=z) return ask4(x[k].s[0],z);
    else return x[k].z1;
}
void ask5(int k,int z){
    if(!k) return;
    if(x[k].z1<z) ans=x[k].z1,ask5(x[k].s[1],z);
    else ask5(x[k].s[0],z);
}
void ask6(int k,int z){
    if(!k) return;
    if(x[k].z1>z) ans=x[k].z1,ask6(x[k].s[0],z);
    else ask6(x[k].s[1],z);
}
int main(){
    int t,rt=0;
    scanf("%d",&t);
    srand(t);
    while(t--){
        int opt,a;
        scanf("%d%d",&opt,&a);
        if(opt==1) cr(rt,a);
        else if(opt==2) de(rt,a);
        else if(opt==3) printf("%d\n",ask3(rt,a)+1);
        else if(opt==4) printf("%d\n",ask4(rt,a));
        else{
            opt==5?ask5(rt,a):ask6(rt,a);
            printf("%d\n",ans);
        }
    }
    return 0;
}