题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

 

输出格式：

 

输出包含若干行整数，即为所有操作3的结果。

 

输入输出样例

输入样例#1： 复制 
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
输出样例#1： 复制 
17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

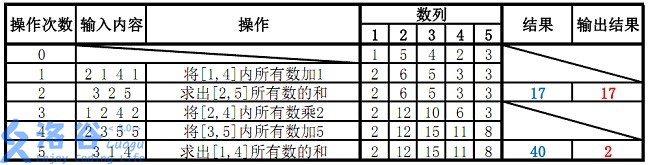
故输出应为17、2（40 mod 38=2）

首先是乘法和加法都是不受%运算位置影响的，也就是说可以在过程中取模和在最后取模效果相同，不过在过程中取模能把数值控制在0~P-1的范围内

这里对于线段树的操作与之前有所不同

对于当前所给的乘法和加法标记，我们考虑在pushdown的时候先下推乘法标记，如果此时子节点已经有了加法和乘法标记，此时我们需要把乘法标记和加法标记都乘上此标记，

因为之前给的加法标记也会受到影响，然后对于子节点做一个更新。

如果是下推加法标记，此时则对乘法标记不会有影响，直接让加法标记加上对应的值即可。

我们在add的时候也是与pushdown类似

#include<cstdio>
#define ls x<<1
#define rs x<<1|1
typedef long long ll;
const ll N=100005;
ll tr[N<<2],lz1[N<<2],lz2[N<<2],bh,ql,qr,a,p;
void bt(ll x,ll l,ll r)
{
    if(l==r) scanf("%lld",&tr[x]);
    else
    {
        ll mid=(l+r)>>1;
        bt(ls,l,mid);
        bt(rs,mid+1,r);
        tr[x]=tr[ls]+tr[rs]; 
    }
}
void pd(ll x,ll l,ll r,ll mid)
{
    if(lz1[x]!=1) 
    {
        lz1[ls]=lz1[ls]*lz1[x]%p;//对于左右儿子分别下推乘法标记 
        lz2[ls]=lz2[ls]*lz1[x]%p;
        tr[ls]=tr[ls]*lz1[x]%p;
        lz1[rs]=lz1[rs]*lz1[x]%p;
        lz2[rs]=lz2[rs]*lz1[x]%p;
        tr[rs]=tr[rs]*lz1[x]%p;
        lz1[x]=1;
    }
    if(lz2[x])
    {
        lz2[ls]=(lz2[ls]+lz2[x])%p;
        tr[ls]=(lz2[x]*(mid-l+1)+tr[ls])%p;
        lz2[rs]=(lz2[rs]+lz2[x])%p;
        tr[rs]=(lz2[x]*(r-mid)+tr[rs])%p;
        lz2[x]=0;
    }
}
void add(ll x,ll l,ll r)
{
    if(ql<=l&&qr>=r) 
    {
        if(bh==1)
        {
            lz1[x]=lz1[x]*a%p;
            lz2[x]=lz2[x]*a%p;
            tr[x]=tr[x]*a%p;//给这区间添加乘法标记时也要给加法标记乘上此数 
        }
        else
        {
            lz2[x]=(lz2[x]+a)%p;
            tr[x]=(a*(r-l+1)+tr[x])%p;
        }
    }
    else
    {
        ll mid=(l+r)>>1;
        pd(x,l,r,mid);
        if(ql<=mid) add(ls,l,mid);
        if(mid<qr) add(rs,mid+1,r);
        tr[x]=tr[ls]+tr[rs];
    }
}
ll ask(ll x,ll l,ll r)
{
    if(ql<=l&&qr>=r) return tr[x];
    else
    {
        ll mid=(l+r)>>1,re=0;
        pd(x,l,r,mid);
        if(ql<=mid) re=(re+ask(ls,l,mid))%p;
        if(mid<qr) re=(re+ask(rs,mid+1,r))%p;
        return re;
    }
}
int main()
{
    ll n,m;
    scanf("%lld%lld%lld",&n,&m,&p);
    for(ll i=1;i<N<<2;++i) lz1[i]=1;//为了应对可能出现的乘0情况，要先把乘法标记都变为1 
    bt(1,1,n);
    while(m--)
    {
        scanf("%lld%lld%lld",&bh,&ql,&qr);
        if(bh==3) printf("%lld\n",ask(1,1,n));
        else
        {
            scanf("%lld",&a);
            add(1,1,n);
        }
    }
    return 0;
}