最大子段和问题,最大子矩阵和问题,最大m子段和问题
1、最大子段和问题
问题定义:对于给定序列a1,a2,a3……an,寻找它的某个连续子段,使得其和最大。如( -2,11,-4,13,-5,-2 )最大子段是{ 11,-4,13 }其和为20。
(1)枚举法求解
枚举法思路如下:
以a[0]开始: {a[0]}, {a[0],a[1]},{a[0],a[1],a[2]}……{a[0],a[1],……a[n]}共n个
以a[1]开始: {a[1]}, {a[1],a[2]},{a[1],a[2],a[3]}……{a[1],a[2],……a[n]}共n-1个
……
以a[n]开始:{a[n]}共1个
一共(n+1)*n/2个连续子段,使用枚举,那么应该可以得到以下算法:
具体代码如下:
//3d4-1 最大子段和问题的简单算法 #include "stdafx.h" #include <iostream> using namespace std; int MaxSum(int n,int *a,int& besti,int& bestj); int main() { int a[] = {-2,11,-4,13,-5,-2}; for(int i=0; i<6; i++) { cout<<a[i]<<" "; } int besti,bestj; cout<<endl; cout<<"数组a的最大连续子段和为:a["<<besti<<":"<<bestj<<"]:"<<MaxSum(6,a,besti,bestj)<<endl; return 0; } int MaxSum(int n,int *a,int& besti,int& bestj) { int sum = 0; for(int i=0; i<n; i++)//控制求和起始项 { for(int j=i; j<n; j++)//控制求和结束项 { int thissum = 0; for(int k=i; k<=j; k++)//求和 { thissum += a[k]; } if(thissum>sum)//求最大子段和 { sum = thissum; besti = i; bestj = j; } } } return sum; }
从这个算法的三个for循环可以看出,它所需要的计算时间是O(n^3)。事实上,如果注意到 ,则可将算法中的最后一个for循环省去,避免重复计算,从而使算法得以改进。改进后的代码如下:
,则可将算法中的最后一个for循环省去,避免重复计算,从而使算法得以改进。改进后的代码如下:
//3d4-2 最大子段和问题的避免重复的简单算法 #include "stdafx.h" #include <iostream> using namespace std; int MaxSum(int n,int *a,int& besti,int& bestj); int main() { int a[] = {-2,11,-4,13,-5,-2}; for(int i=0; i<6; i++) { cout<<a[i]<<" "; } int besti,bestj; cout<<endl; cout<<"数组a的最大连续子段和为:a["<<besti<<":"<<bestj<<"]:"<<MaxSum(6,a,besti,bestj)<<endl; return 0; } int MaxSum(int n,int *a,int& besti,int& bestj) { int sum = 0; for(int i=0; i<n; i++)//控制求和起始项 { int thissum = 0; for(int j=i; j<=n; j++)//控制求和结束项 { thissum += a[j];//求和 if(thissum>sum) { sum = thissum; besti = i; bestj = j; } } } return sum; }
(2)分治法求解
分治法思路如下:
将序列a[1:n]分成长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大字段和,则a[1:n]的最大子段和有三中情形:
[1]、a[1:n]的最大子段和与a[1:n/2]的最大子段和相同;
[2]、a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同;
[3]、a[1:n]的最大字段和为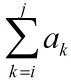 ,且1<=i<=n/2,n/2+1<=j<=n。
,且1<=i<=n/2,n/2+1<=j<=n。
可用递归方法求得情形[1],[2]。对于情形[3],可以看出a[n/2]与a[n/2+1]在最优子序列中。因此可以在a[1:n/2]中计算出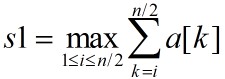 ,并在a[n/2+1:n]中计算出
,并在a[n/2+1:n]中计算出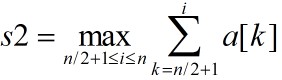 。则s1+s2即为出现情形[3]时的最优值。
。则s1+s2即为出现情形[3]时的最优值。
具体代码如下:
//3d4-1 最大子段和问题的分治算法 #include "stdafx.h" #include <iostream> using namespace std; int MaxSubSum(int *a,int left,int right); int MaxSum(int n,int *a); int main() { int a[] = {-2,11,-4,13,-5,-2}; for(int i=0; i<6; i++) { cout<<a[i]<<" "; } cout<<endl; cout<<"数组a的最大连续子段和为:"<<MaxSum(6,a)<<endl; return 0; } int MaxSubSum(int *a,int left,int right) { int sum = 0; if(left == right) { sum = a[left]>0?a[left]:0; } else { int center = (left+right)/2; int leftsum = MaxSubSum(a,left,center); int rightsum = MaxSubSum(a,center+1,right); int s1 = 0; int lefts = 0; for(int i=center; i>=left;i--) { lefts += a[i]; if(lefts>s1) { s1=lefts; } } int s2 = 0; int rights = 0; for(int i=center+1; i<=right;i++) { rights += a[i]; if(rights>s2) { s2=rights; } } sum = s1+s2; if(sum<leftsum) { sum = leftsum; } if(sum<rightsum) { sum = rightsum; } } return sum; } int MaxSum(int n,int *a) { return MaxSubSum(a,0,n-1); }
算法所需的计算时间T(n)满足一下递归式:
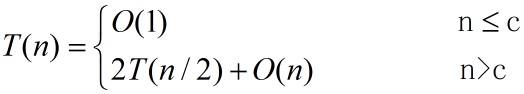
解此递归方程可知:T(n)=O(nlogn)。
(3)动态规划算法求解
算法思路如下:
记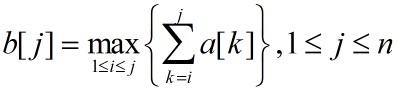 ,则所求的最大子段和为:
,则所求的最大子段和为: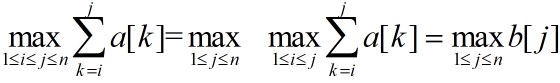
由b[j]的定义知,当b[j-1]>0时,b[j]=b[j-1]+a[j],否则b[j]=a[j]。由此可得b[j]的动态规划递推式如下:
b[j]=max{b[j-1]+a[j],a[j]},1<=j<=n。
具体代码如下:
//3d4-1 最大子段和问题的动态规划算法 #include "stdafx.h" #include <iostream> using namespace std; int MaxSum(int n,int *a); int main() { int a[] = {-2,11,-4,13,-5,-2}; for(int i=0; i<6; i++) { cout<<a[i]<<" "; } cout<<endl; cout<<"数组a的最大连续子段和为:"<<MaxSum(6,a)<<endl; return 0; } int MaxSum(int n,int *a) { int sum=0,b=0; for(int i=1; i<=n; i++) { if(b>0) { b+=a[i]; } else { b=a[i]; } if(b>sum) { sum = b; } } return sum; }
上述算法的时间复杂度和空间复杂度均为O(n)。
2、最大子矩阵和问题
(1)问题描述:给定一个m行n列的整数矩阵A,试求A的一个子矩阵,使其各元素之和为最大。
(2)问题分析:
用二维数组a[1:m][1:n]表示给定的m行n列的整数矩阵。子数组a[i1:i2][j1:j2]表示左上角和右下角行列坐标分别为(i1,j1)和(i2,j2)的子矩阵,其各元素之和记为: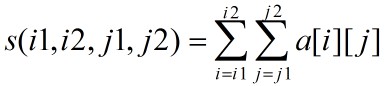
最大子矩阵问题的最优值为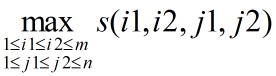 。如果用直接枚举的方法解最大子矩阵和问题,需要O(m^2n^2)时间。注意到
。如果用直接枚举的方法解最大子矩阵和问题,需要O(m^2n^2)时间。注意到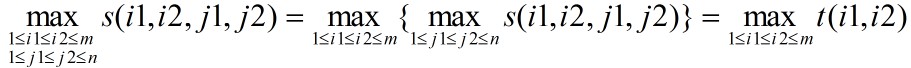 ,式中,
,式中,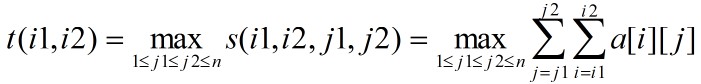 ,设
,设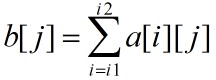 ,则
,则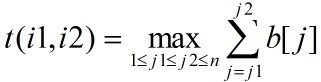
容易看出,这正是一维情形的最大子段和问题。因此,借助最大子段和问题的动态规划算法MaxSum,可设计出最大子矩阵和动态规划算法如下:
//3d4-5 最大子矩阵之和问题 #include "stdafx.h" #include <iostream> using namespace std; const int M=4; const int N=3; int MaxSum(int n,int *a); int MaxSum2(int m,int n,int a[M][N]); int main() { int a[][N] = {{4,-2,9},{-1,3,8},{-6,7,6},{0,9,-5}}; for(int i=0; i<M; i++) { for(int j=0; j<N; j++) { cout<<a[i][j]<<" "; } cout<<endl; } cout<<endl; cout<<"数组a的最大连续子段和为:"<<MaxSum2(M,N,a)<<endl; return 0; } int MaxSum2(int m,int n,int a[M][N]) { int sum = 0; int *b = new int[n+1]; for(int i=0; i<m; i++)//枚举行 { for(int k=0; k<n;k++) { b[k]=0; } for(int j=i;j<m;j++)//枚举初始行i,结束行j { for(int k=0; k<n; k++) { b[k] += a[j][k];//b[k]为纵向列之和 int max = MaxSum(n,b); if(max>sum) { sum = max; } } } } return sum; } int MaxSum(int n,int *a) { int sum=0,b=0; for(int i=1; i<=n; i++) { if(b>0) { b+=a[i]; } else { b=a[i]; } if(b>sum) { sum = b; } } return sum; }
以上代码MaxSum2方法的执行过程可用下图表示:
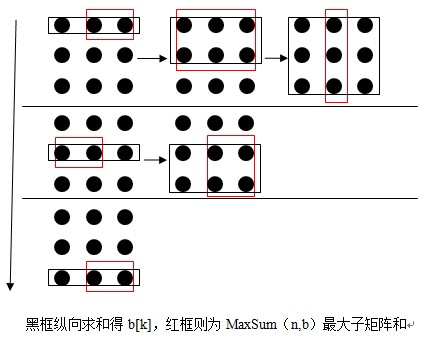
3、最大m子段和问题
(1)问题描述:给定由n个整数(可能为负数)组成的序列a1,a2,a3……an,以及一个正整数m,要求确定此序列的m个不相交子段的总和达到最大。最大子段和问题是最大m字段和问题当m=1时的特殊情形。
(2)问题分析:设b(i,j)表示数组a的前j项中i个子段和的最大值,且第i个子段含a[j](1<=i<=m,i<=j<=n),则所求的最优值显然为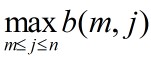 。与最大子段问题相似,计算b(i,j)的递归式为:
。与最大子段问题相似,计算b(i,j)的递归式为: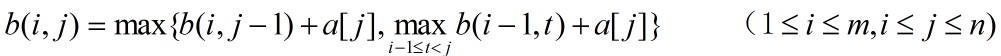
其中,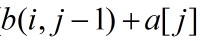 表示第i个子段含a[j-1],而
表示第i个子段含a[j-1],而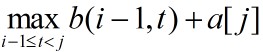 项表示第i个子段仅含a[j]。初始时,b(0,j)=0,(1<=j<=n);b(i,0)=0,(1<=i<=m)。
项表示第i个子段仅含a[j]。初始时,b(0,j)=0,(1<=j<=n);b(i,0)=0,(1<=i<=m)。
具体代码如下:
//3d4-6 最大m子段问题 #include "stdafx.h" #include <iostream> using namespace std; int MaxSum(int m,int n,int *a); int main() { int a[] = {0,2,3,-7,6,4,-5};//数组脚标从1开始 for(int i=1; i<=6; i++) { cout<<a[i]<<" "; } cout<<endl; cout<<"数组a的最大连续子段和为:"<<MaxSum(3,6,a)<<endl; } int MaxSum(int m,int n,int *a) { if(n<m || m<1) return 0; int **b = new int *[m+1]; for(int i=0; i<=m; i++) { b[i] = new int[n+1]; } for(int i=0; i<=m; i++) { b[i][0] = 0; } for(int j=1;j<=n; j++) { b[0][j] = 0; } //枚举子段数目,从1开始,迭代到m,递推出b[i][j]的值 for(int i=1; i<=m; i++) { //n-m+i限制避免多余运算,当i=m时,j最大为n,可据此递推所有情形 for(int j=i; j<=n-m+i; j++) { if(j>i) { b[i][j] = b[i][j-1] + a[j];//代表a[j]同a[j-1]一起,都在最后一子段中 for(int k=i-1; k<j; k++) { if(b[i][j]<b[i-1][k]+a[j]) b[i][j] = b[i-1][k]+a[j];//代表最后一子段仅包含a[j] } } else { b[i][j] = b[i-1][j-1]+a[j];//当i=j时,每一项为一子段 } } } int sum = 0; for(int j=m; j<=n; j++) { if(sum<b[m][j]) { sum = b[m][j]; } } return sum; }
上述算法的时间复杂度为O(mn^2),空间复杂度为O(mn)。其实,上述算法中,计算b[i][j]时,只用到了数组b的第i-1行和第i行的值。因而,算法中只要存储数组b的当前行,不必存储整个数组。另一方面,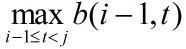 的值可以在计算i-1行时预先计算并保存起来。计算第i行的值时不必重新计算,节省了计算时间和空间。因此,算法可继续改进如下:
的值可以在计算i-1行时预先计算并保存起来。计算第i行的值时不必重新计算,节省了计算时间和空间。因此,算法可继续改进如下:
//3d4-7 最大m子段问题 #include "stdafx.h" #include <iostream> using namespace std; int MaxSum(int m,int n,int *a); int main() { int a[] = {0,2,3,-7,6,4,-5};//数组脚标从1开始 for(int i=1; i<=6; i++) { cout<<a[i]<<" "; } cout<<endl; cout<<"数组a的最大连续子段和为:"<<MaxSum(3,6,a)<<endl; } int MaxSum(int m,int n,int *a) { if(n<m || m<1) return 0; int *b = new int[n+1]; int *c = new int[n+1]; b[0] = 0;//b数组记录第i行的最大i子段和 c[1] = 0;//c数组记录第i-1行的最大i-1子段和 for(int i=1; i<=m; i++) { b[i] = b[i-1] + a[i]; c[i-1] = b[i]; int max = b[i]; //n-m+i限制避免多余运算,当i=m时,j最大为n,可据此递推所有情形 for(int j=i+1; j<=i+n-m;j++) { b[j] = b[j-1]>c[j-1]?b[j-1]+a[j]:c[j-1]+a[j]; c[j-1] = max;//预先保存第j-1行的最大j-1子段和 if(max<b[j]) { max = b[j]; } } c[i+n-m] = max; } int sum = 0; for(int j=m; j<=n; j++) { if(sum<b[j]) { sum = b[j]; } } return sum; }
上述算法时间复杂度为O(m(n-m)),空间复杂度为O(n)。当m或n-m为常数时,时间复杂度和空间复杂度均为O(n)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号