mAP(mean Average Precision)应用(转)
1. precision 和 recall 的计算（没什么好说的，图片示例相当棒）：
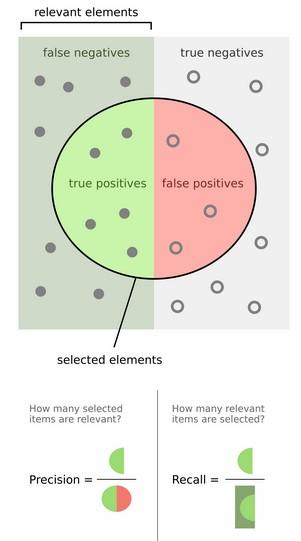图1
图中上部分，左边一整个矩形中（false negative和true positive）的数表示ground truth之中为1的（即为正确的）数据，右边一整个矩形中的数表示ground truth之中为0的数据。
精度precision的计算是用 检测正确的数据个数/总的检测个数。
召回率recall的计算是用 检测正确的数据个数/ground truth之中所有正数据个数。
2. AP：average precision
假设我们有数据（原数据缺失并有错。根据个人理解进行补充，红色为出错部分，绿色为缺失部分）：
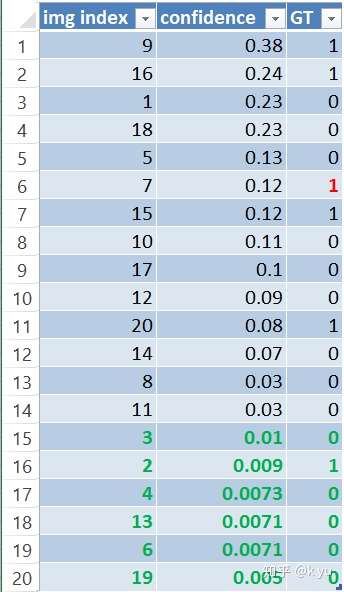图2
一共20个图像，20行，第一列是图像index， 第二列是检测confidence， 第三列是ground truth。根据confidence从大到小排列。
每检测一个图像时，无论是正例还是负例，计算当下的precision和recall。
假设检测样本中每N个样本中有M个正例，那么我们会得到M个recall值（1/M, 2/M, ..., M/M）（由于检测N'数量正样本时，precision有不同情况）,对于每个recall值r，我们可以计算出对应（r' >= r）的最大precision，然后对这些max precision取平均即得到最后的AP值。具体计算如图，top-N是指根据confidence降级排列后样本的排位号（eg. 1为confidence最大的图像9）：
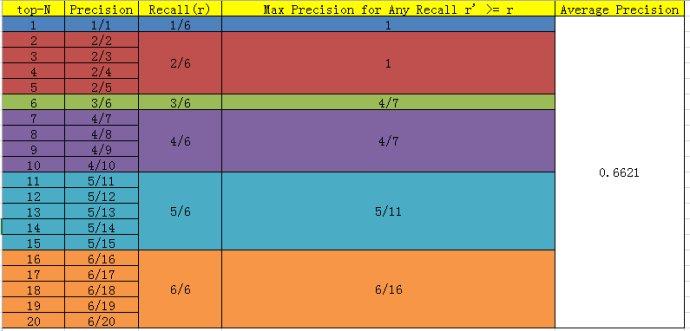图3
补充解释：
一共20个图像，GT为True的共6个图像，img_index分别是9, 16, 7（纠正），15, 20和2（补充）。
在图2中从上往下依次计算得图3结果：
排位号1:
精度=TP个数/已经选择的样本数=1/1；
召回率=TP个数/所有GT为True的样本数=1/6；
当召回率大于等于1/6时，最大精度=那就是1，也就是100%没有比100%更大的数值了
排位号2:
精度=TP个数/已经选择的样本数=2/2；
召回率=TP个数/所有GT为True的样本数=2/6；
当召回率大于等于2/6时，最大精度=仍然是1，也就是100%没有比100%更大的数值了
排位号6:
精度=TP个数/已经选择的样本数=3/6；
召回率=TP个数/所有GT为True的样本数=3/6；
当召回率大于等于3/6时，最大精度：先看召回率大于等于3/6时，所有精度有哪些，有精度：3/6， 4/7， 4/8， 4/9， 4/10， 5/11， 5/12， 5/13， 5/14， 5/15， 6/16， 6/17， 6/18， 6/19， 6/20。取最大 精度4/7
排位号7:
精度=TP个数/已经选择的样本数=4/7；
召回率=TP个数/所有GT为True的样本数=4/6；
当召回率大于等于4/6时，最大精度：先看召回率大于等于4/6时，所有精度有哪些，有精度：4/7， 4/8， 4/9， 4/10， 5/11， 5/12， 5/13， 5/14， 5/15， 6/16， 6/17， 6/18， 6/19， 6/20。取最大 精度4/7
排位号11:
精度=TP个数/已经选择的样本数=5/11；
召回率=TP个数/所有GT为True的样本数=5/6；
当召回率大于等于5/6时，最大精度：先看召回率大于等于5/6时，所有精度有哪些，有精度：5/11， 5/12， 5/13， 5/14， 5/15， 6/16， 6/17， 6/18， 6/19， 6/20。取最大 精度5/11
其余排位号不在列举。
AP = （1 +１＋４/７＋４/７＋５/１１＋６/１６）／６ ＝ ０．６６２１
3. mAP: mean average precision
多类的检测中，取每个类AP的平均值，即为mAP。
