ResNet详解(转)
本篇文章涉及到的文献
- Residual Network(ResNet)
- Deep Residual Learning for Image Recognition[arXiv:1512.03385]
- Identity Mappings in Deep Residual Networks[arXiv:1603.05027]
- 2016_tutorial_deep_residual_networks
- ResNet-50 Architecture
- KaimingHe/deep-residual-networks
- CS231n 2017 lecture9
- BIGBALLON/cifar-10-cnn
妹纸:昨天试了一下VGG19,训练时间挺久的,不过效果不错。
花花:呜呜,前几天我们都在讲很基本的网络架构,今天我们讲稍微难一丢丢的。
妹纸:好啊,好啊!我猜是ResNet!
花花:你猜得真准(23333orz)。
最原始的 Residual Network
Residual Network,简称 ResNet(残差网络),是MSRA 何凯明 团队设计的一种网络架构,在2015年的ILSVRC 和 COCO 上拿到了多项冠军,其发表的论文Deep Residual Learning for Image Recognition, 是 CVPR 2016 的最佳论文。
Residual Network的历史从这里开始。
卷积神经网络(Convolutional Neural Network)正不断朝着“Deep”这个方向发展,最早期的LeNet只有5层,后来VGG把深度增加到19层,而我们即将要介绍的ResNet,更是超过了100层。
人们不禁要问:
Is learning better networks as easy as stacking more layers?
不,事实并非如此
只是简单地增加网路的深度,不能得到很好的效果,甚至还会使误差增大:

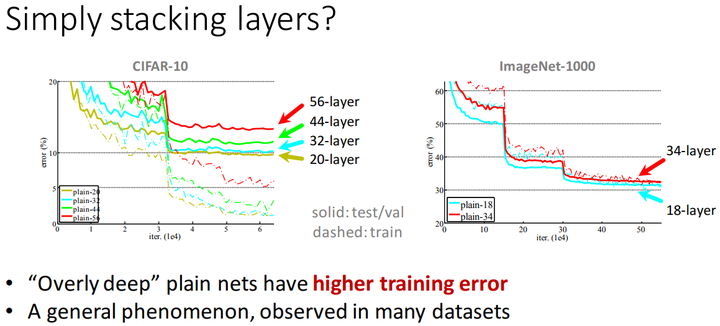
多个datasets的测试表明,仅仅只是简单地堆叠卷积层,并不能让网络训练得更好。
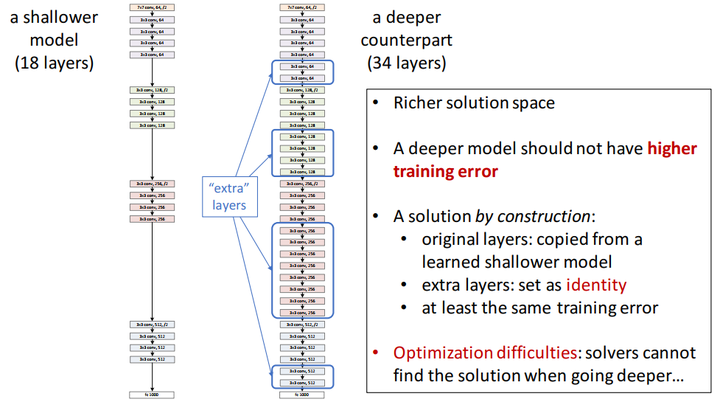
按理来说,如果网络加深,training acc应该增大,而testing acc减小,但是上图并不是这么回事,于是乎,Kaiming He提出了Deep Residual Learning的架构。
关于残差模块(residual block)
这里Kaiming聚聚首先引入了一个残差模块(residual block)的概念
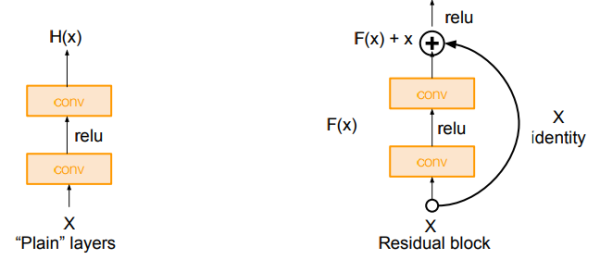
上图所示的Residual Block:
输入为 ,需要拟合的结果(输出)为
。
那么我们把输出差分为 ,也就是
再令 ,意思是
也是由
拟合而来,
那么最后的输出就变为 本来就是输入,
所以我们就只需要拟合 就好了。
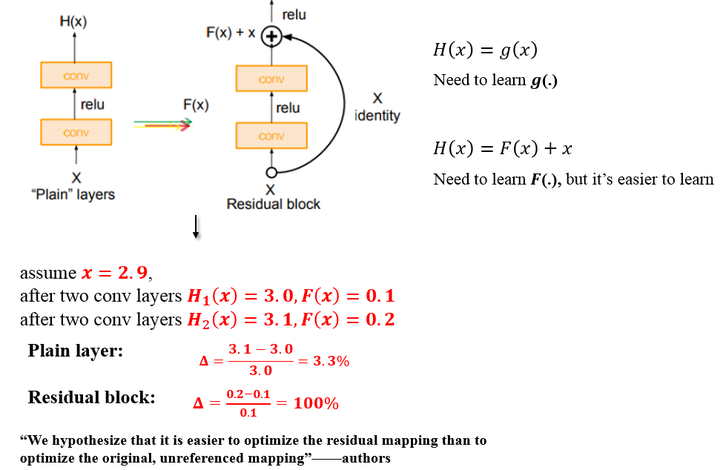
如上图,原始的plain架构,我们用两层卷积层来模拟函数 ,
而在residual block中,我们用两层卷积层来模拟函数
举个例子:
输入 , 经过拟合后的输出为
那么残差就是
如果拟合的是恒等变换,即输入 ,输出还是
那么残差就是
而如上图所示,假设 从
经过两层卷基层(conv)之后变为
,
平原网络的变化率
而残差模块的变化率为
残差的引入去掉了主体部分,从而突出了微小的变化。我想这是他们敢说
We hypothesize that it is easier to optimize the residual mapping than to optimize
the original, unreferenced mapping
的原因。
有了残差模块(residual block)这个概念,我们再来设计网络架构,
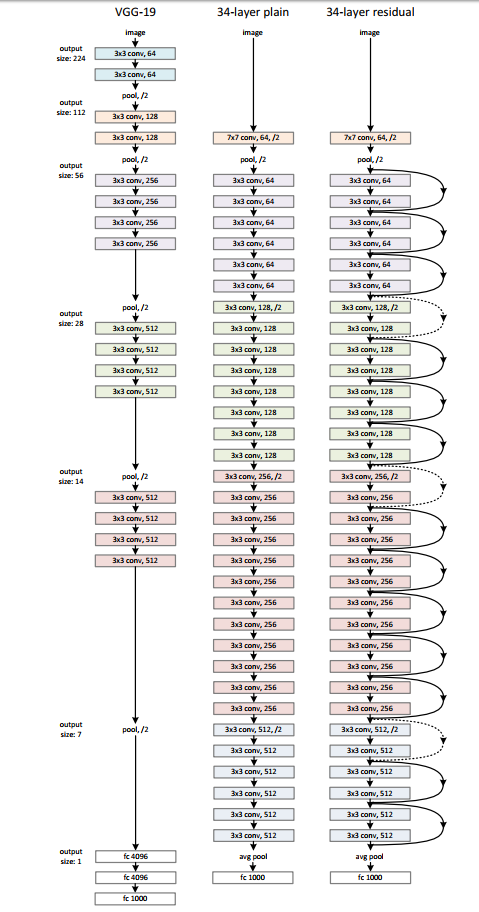
架构很简单,基于VGG19的架构,我们首先把网络增加到34层,增加过后的网络我们叫做plain network,再此基础上,增加残差模块,得到我们的Residual Network
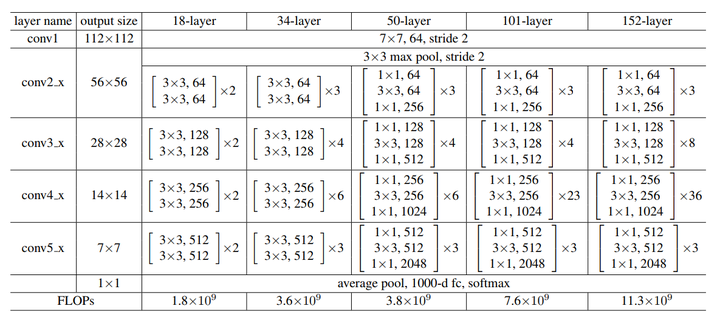
关于bottleneck
论文中有两种residual block的设计,如下图所示:
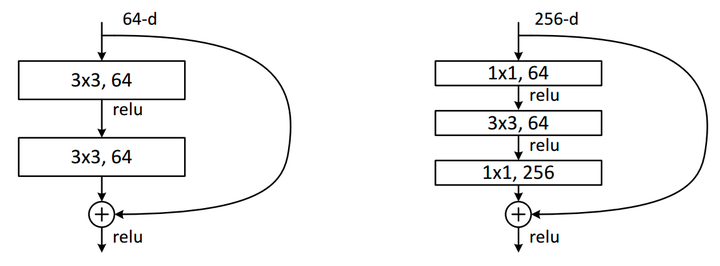
在训练浅层网络的时候,我们选用前面这种,而如果网络较深(大于50层)时,会考虑使用后面这种(bottleneck),这两个设计具有相似的时间复杂度。
同样举个例子:
对于ImageNet而言,进入到第一个residual block的input为
采用左侧的两个 的卷积层:
参数量为
化简一下:
采用右侧的bottleneck:
参数量为
化简一下:
可以看到它们的参数量属于同一个量级,
但是这里bottleneck占用了整个network的「三层」,而原本只有「两层」,
所以这样就节省了大量的参数,
在大于50层的resnet中,他们使用了bottleneck这种形式。
具体细节如图所示:
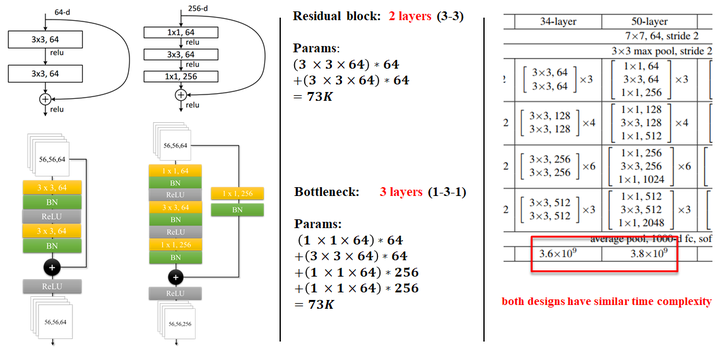
如果你还有问题,参考这里 ResNet之Deeper Bottleneck Architectures
Identity mapping 改进
Kaiming He最初的paper,就是上面介绍的部分,但很快,他们又对ResNet提出了进一步的改进,这便是我们接下来要提到的paper:
Identity Mappings in Deep Residual Networks[arXiv:1603.05027]
我们来仔细分析一下Residual Block, 在这篇paper中也被叫为Residual Unit.
对于原始的 Residual Unit(block),我们有如下计算:
表示 第
个Residual Unit的输入,
则代表 第
个Residual Unit的输出
代表的某个变换,在这里是恒等变换,
代表residual function,
代表某种操作,在这里是ReLU
所以可以写成如下形式:

也就是Residual Unit一开始的做法了。
那如果,我们 是恒等变换呢,即
,那么有:
对于任意一层,我们都能用这个公式来表示:
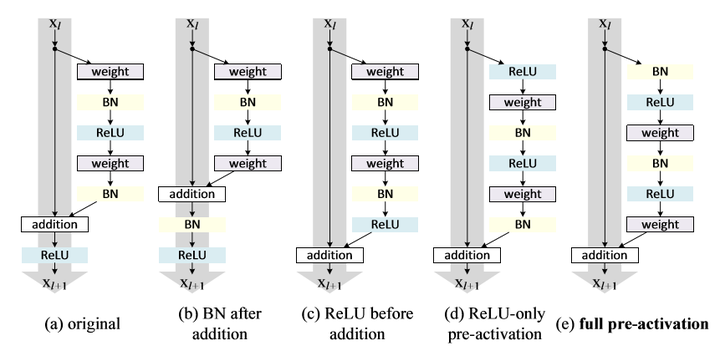
这便是这篇paper的改进,把原本的ReLU,放到Residual Unit的conv前面去,而不是放在addition之后。
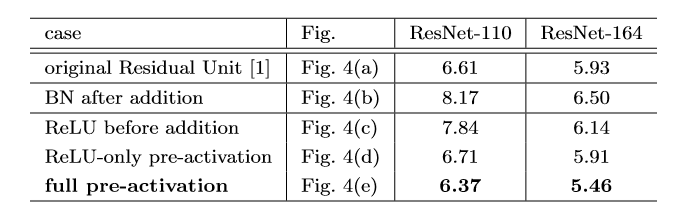
可以看到,在上图作者对cifar10进行的多组实验中,使用full pre-activation这种Residul Unit效果最佳,个人认为这张表格还是挺重要的,我们简单分析一下!
- (a)original:原始的结构
- (b)BN after addition:这是在做相反的实验,本来我们的目的是把ReLU移到旁路上去,这里反而把BN拿出来,这进一步破坏了主路线上的恒等关系,阻碍了信号的传递,从结果也很容易看出,这种做法不ok
- (c)ReLU before addition:将
变为恒等变换,最容易想到的方法就是将ReLU直接移动到BN后面,但这会出现一个问题,一个
(残差函数)的输出应该可以是
,但是经过ReLU之后就会变为
,这种做法的结果,也比(a)要差。
直接提上来似乎不行,但是问题反过来想, 在addition之后做ReLU,不是相当于在下一次conv之前做ReLU吗?
- (d)ReLU-only pre-activation:根据刚才的想法,我们把ReLU放到前面去,然而我们得到的结果和(a)差不多,原因是什么呢?因为这个ReLU层不与BN层连接使用,因此无法共享BN所带来的好处。
- (e)full pre-activation:啊,那要不我们也把BN弄前面去,惊喜出现了,我们得到了相当可观的结果,是的,这便是我们最后要使用的Unit结构!!!
代码实现
终于到了可以写代码的时候了,
还是放在我的 Github,测试只是用了50层,
使用GTX980TI,训练时间为 8 h 58 min
最后testing accuracy:94.10%
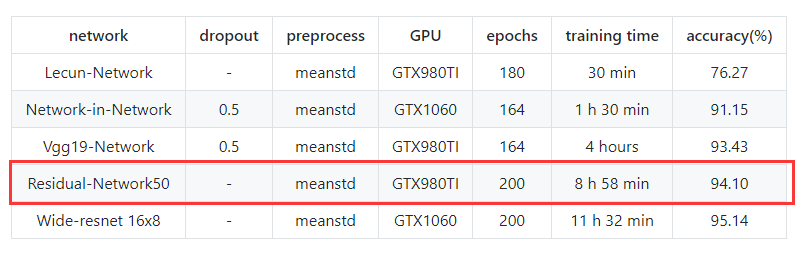
妹纸:哇,ResNet的residual block好帅气啊,何凯明简直是我男神!
花花:喔,他是所有人心中的男神!
妹纸:要训练9个小时啊,我周末试一下啊
花花:你的是1080TI,训练个毛9小时,我980TI才要9小时啊!!
妹纸:啊,反正是学长给配的
花花:啊,2333


 浙公网安备 33010602011771号
浙公网安备 33010602011771号