[leetcode] 141. Linked List Cycle
题目大意
判断单链表中是否存在环
#!/usr/bin/env python # coding=utf-8 # Date: 2018-08-31 """ https://leetcode.com/problems/linked-list-cycle/description/ 141. Linked List Cycle Given a linked list, determine if it has a cycle in it. Follow up: Can you solve it without using extra space? """ # Definition for singly-linked list. class ListNode(object): def __init__(self, x): self.val = x self.next = None class Solution(object): def hasCycle(self, head): """ :type head: ListNode :rtype: bool """
解题思路
Approach 1: Hash Table 哈希表
Intuition
To detect if a list is cyclic, we can check whether a node had been visited before. A natural way is to use a hash table.
Algorithm
We go through each node one by one and record each node's reference (or memory address) in a hash table. If the current node is null, we have reached the end of the list and it must not be cyclic. If current node’s reference is in the hash table, then return true.
Java解法:
public boolean hasCycle(ListNode head) { Set<ListNode> nodesSeen = new HashSet<>(); while (head != null) { if (nodesSeen.contains(head)) { return true; } else { nodesSeen.add(head); } head = head.next; } return false; }
Python解法:
class Solution(object): def hasCycle(self, head): # Hash Table """ :type head: ListNode :rtype: bool """ visited = set() while head: if head in visited: return True else: visited.add(head) head = head.next return False
Complexity analysis
Time complexity : O(n)O(n). We visit each of the nn elements in the list at most once. Adding a node to the hash table costs only O(1)O(1) time.
Space complexity: O(n)O(n). The space depends on the number of elements added to the hash table, which contains at most nn elements.
Approach 2: Two Pointers 快慢指针
Intuition
Imagine two runners running on a track at different speed. What happens when the track is actually a circle?
Algorithm
The space complexity can be reduced to O(1)O(1) by considering two pointers at different speed - a slow pointer and a fast pointer. The slow pointer moves one step at a time while the fast pointer moves two steps at a time.
If there is no cycle in the list, the fast pointer will eventually reach the end and we can return false in this case.
Now consider a cyclic list and imagine the slow and fast pointers are two runners racing around a circle track. The fast runner will eventually meet the slow runner. Why? Consider this case (we name it case A) - The fast runner is just one step behind the slow runner. In the next iteration, they both increment one and two steps respectively and meet each other.
How about other cases? For example, we have not considered cases where the fast runner is two or three steps behind the slow runner yet. This is simple, because in the next or next's next iteration, this case will be reduced to case A mentioned above.
Java解法:
public boolean hasCycle(ListNode head) { if (head == null || head.next == null) { return false; } ListNode slow = head; ListNode fast = head.next; while (slow != fast) { if (fast == null || fast.next == null) { return false; } slow = slow.next; fast = fast.next.next; } return true; }
Python解法:
class Solution(object): def hasCycle(self, head): # Two Pointers """ :type head: ListNode :rtype: bool """ if not head or not head.next: return False slow, fast = head, head.next while slow != fast: if not fast or not fast.next: return False slow, fast = slow.next, fast.next.next return True
Complexity analysis
- Time complexity : O(n)O(n). Let us denote nn as the total number of nodes in the linked list. To analyze its time complexity, we consider the following two cases separately.
- List has no cycle:
The fast pointer reaches the end first and the run time depends on the list's length, which is O(n)O(n).
-
- List has a cycle:
We break down the movement of the slow pointer into two steps, the non-cyclic part and the cyclic part:
- The slow pointer takes "non-cyclic length" steps to enter the cycle. At this point, the fast pointer has already reached the cycle.
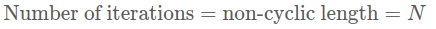
- Both pointers are now in the cycle. Consider two runners running in a cycle - the fast runner moves 2 steps while the slow runner moves 1 steps at a time. Since the speed difference is 1, it takes
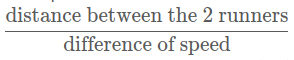
loops for the fast runner to catch up with the slow runner. As the distance is at most "cyclic length K" and the speed difference is 1, we conclude that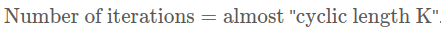
- The slow pointer takes "non-cyclic length" steps to enter the cycle. At this point, the fast pointer has already reached the cycle.
Therefore, the worst case time complexity is O(N+K)O(N+K), which is O(n)O(n).
- Space complexity : O(1)O(1). We only use two nodes (slow and fast) so the space complexity is O(1)O(1).
参考:https://leetcode.com/problems/linked-list-cycle/solution/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号