201971010259-张圆圆 实验三 结对项目—《{0-1}KP 实例数据集算法实验平台》项目报告
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 2022年春软件工程课程班(2019级计算机科学与技术) |
| 作业要求链接 | 实验三 软件工程结对项目 |
| 我的课程学习目标 | * 仔细阅读《构建之法》,理解并掌握代码风格规范、代码设计规范、代码复审、结对编程概念 * 体验软件项目开发中的两人合作,练习结对编程(Pair programming) * 掌握Github协作开发软件的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | * 通过阅读《构建之法》中的第3,4章,对代码风格规范、代码设计规范、代码复审、结对编程等概念有了更加深入的了解 * 通过两人结伴编程项目,体验了软件项目开发中的两人合作,对结对编程(Pair programming)有了实质性认识 * 通过两人结对编程此次项目,并上传至github,掌握了Github协作开发软件的操作方法。 |
| 结对方学号-姓名 | 201971010116-姜婷 |
| 结对方本次博客作业链接 | 201971010116-姜婷 实验三 结对项目—《{0-1}KP 实例数据集算法实验平台》项目报告 |
| 项目Github的仓库链接地址 | Knapsack-0-1 |
任务1:阅读《现代软件工程—构建之法》第3-4章内容,理解掌握代码风格规范、代码设计规范、代码复审、结对编程概念#
《现代软件工程—构建之法》第3章#
- 软件工程师的成长
- 积累软件开发相关的知识,提升技术技能,对具体技术的掌握,动手能力。
- 积累问题领域的知识和经验。
- 对通用的软件设计思想和软件工程思想的理解。
- 提升职业技能(其区别于技术技能)。
- 软件流程TSP
- 交流:有效地和其他队员交流,从大的技术方向,到看似微小的问题。
- 说到做到:团队成员要做到“按时交付”。
- 接受团队赋予的角色并按角色要求工作:团队要完成任务,有很多事情要做,要接受不同的任务并高质量完成。
- 全力投入团队的活动:对于团队任务及活动,都要全力以赴地参加,而不是游离于团队之外。
- 按照团队流程的要求工作:团队有自己的流程,个人的能力要按照团队制定的流程工作,而不要认为自己不受流程约束。
- 准备:在开会讨论之前,开始一个新功能之前,一个新项目之前,都要做好准备工作。
- 理性地工作:软件开发有很多个人的、感情驱动的因素,但是一个成熟的团队成员必须从事实和数据出发,按照流程,理性地工作。
- 软件工程师的思维误区
- 分析麻痹:一种极端情况是想弄清楚所有细节、所有依赖关系之后再动手,心理上过于悲观,不想修复问题,出了问题都赖在相关问题上。
- 不分主次,想解决所有依赖问题:过于积极,想马上动手修复所有主要和次要的
依赖问题,然后就可以“完美地”达成最初设定的目标,而不是根据现有条件找到一个“足够
好”的方案。 - 过早优化:软件有很大的可塑性,可以不断改进。 一个复杂的软件似乎很多模块都可以变得更好。一个工程师在写程序的时候,经常容易在某一个局部问题上陷进去,花大量时间对其进行优化;无视这个模块对全局的重要性,甚至不了解“全局”。
- 过早扩大化/泛化( Premature Generalization):软件可以扩展,但有些软件本来是解决一个特定环境下的具体问题,不适合用于处理所有类似的问题,程序员在解决问题时要了解必要性、难度和时机。
《现代软件工程—构建之法》第4章#
- 代码规范
- 代码风格规范
代码风格的原则是:简明,易读,无二义性,具体代码风格规范如下表所示:
- 代码风格规范
| 代码要求 | 代码规范 |
|---|---|
| 缩进 | * 缩进采用4个空格,可读性好。 * 不用Tab键,是因为Tab键在不同的情况下会显示不同的长度,严重干扰阅读体验。 |
| 行宽 | 限定为100字符 |
| 括号 | * 在复杂的条件表达式中,用括号清楚地表示逻辑优先级。 |
| 断行与空白的{}行 | * 断行可便于查看各个程序变量的变化情况。 * {}用于判断程序的结构,每个“{”和“}”都独占一行。 |
| 分行 | 不要把多条语句放在一行上。 不要把多个变量定义在一行上。 |
| 命名 | * 在变量名中不要提到类型或其他语法方面的描述。 避免过多的描述。 如果信息可以从上下文中得到,那么此类信息就不必写在变量名中。 * 避免可要可不要的修饰词。 |
| 下划线 | * 用来分割变量名字中的作用域标注和变量的语义。 |
| 大小写 | * 所有类型/类/函数名都用Pascal形式,即所有单词第一个字母都大写。 * 所有变量都用Camel形式,即第一个单词全部小写,随后单词用Pascal形式。 * 类/类型/变量:名词或组合名词。 * 函数用动词或动宾组合词来表示。 |
| 注释 | * 复杂的注释应该放在函数头,很多函数头的注释都用来解释参数的类型等,如果程序正文已经能够说明参数的类型in/out,就不要重复。 * 注释要随着程序的修改而不断更新。 * 注释(包括所有源代码)应该只用ASCII字符,不要用中文或其他特殊字符,否则会极大地影响程序的可移植性。 |
- 代码设计规范
代码设计规范不光是程序书写的格式问题,而且牵涉到程序设计、模块之间的关系、设计模式等方方面面,而这里又有不少内容与具体程序设计语言息息相关(如C、C++、Java、 C#),但是也有通用的原则,具体原则如下表所示:
| 名称 | 代码设计规范原则 |
|---|---|
| 函数 | * 最重要的原则是:只做一件事, 并且要做好。 |
| goto | * 函数最好有单一出口,为了达到这一目的,可以使用goto,有助于程序逻辑的清晰体现。 |
| 错误处理 | * 参数处理:在Debug版本中,所有的参数都要验证其正确性,在正式版本中,对从外部(用户或别的模块)传递过来的参数,要验证其正确性。 * 断言:验证正确性。 |
| 如何处理C++中的类 | 代码设计要求 |
| - 类 | * 使用类来封装面向对象的概念和多态。 * 避免传递类型实体的值,应该用指针传递。对于简单的数据类型,没有必要要用类来实现。 * 对于有显示的构造和析构的类,不要建立全局的实体。 * 仅在有必要时,才是用“类”。 |
| - class vs.struct | * 如果只是数据的封装,用struct即可。 |
| - 公共/保护/私有成员 | * 按照这样的次序来说明类中的成员:public、protected、 private。 |
| - 数据成员 | * 数据类型的成员用m_name说明。 * 不要使用公共的数据成员,要用inline访问函数,可兼顾封装和效率。 |
| - 虚函数 | * 使用虚函数来实现多态。 * 仅在很有必要时,才使用虚函数。 * 如果一个类型要实现多态,在基类中的析构函数应该是虚函数。 |
| - 构造函数 | * 不要在构造函数中做复杂的操作,简单初始化所有成员即可。 * 构造函数不应该返回错误,把可能出错的操作放到HrInit()或FInit()中。 |
| - 析构函数 | * 把所有的清理工作都放在析构函数中,若有些析构函数在之前就释放了,要重置这些成员为0或NULL。 * 析构函数不应该出错。 |
| - new 和 delete | * 若有可能,实现自己的new/delete,可方便地加上自己的跟踪和管理机制。自己的new/delete可以包装系统提供的new/delete。 * 检查new的返回值。new不一定都成功。 * 释放指针时不用检查NULL。 |
| - 运算符 | * 在理想情况下,定义的类不需要自定义操作符。确有必要时,才会自定义操作符。 * 运算符不要做标准语义之外的任何动作。 * 运算符的实现必须非常有效率,若有复杂的操作,应定义一个单独的函数。 * 当拿不定注意时,用成员函数,不要用运算符。 |
| - 异常 | * 不要用异常作为逻辑控制来处理程序的主要流程。 * 了解异常及处理异常的花销。 * 当使用异常时,要注意在什么地方清理数据。 * 异常不能跨过DLL或进程的边界来传递消息,异常不是万能的。 |
| - 类型继承 | * 仅在有必要时,才使用类型继承。 * 用const标注只读的参数。 * 用const标注不改变数据的函数。 |
- 代码复审
- 代码复审的正确定义:看代码是否在代码规范的框架内正确地解决了问题。
- 代码复审的目的:
- 找出代码的错误,如:编码错误,不符合团队代码规范的地方
- 发现逻辑错误,程序可以编译通过,但是代码的逻辑是错的
- 发现算法错误,比如使用的算法不够优化,边界条件没有处理好等
- 发现潜在的错误和回归性错误一当前的修改导致以前修复的缺陷又重新出现
- 发现可能需要改进的地方
- 教育(互相教育)开发人员,传授经验,让更多的成员熟悉项目各部分的代码,同时熟悉和应用领域相关的实际知识
- 代码复审的形式:(见下表)
| 名称 | 形式 | 目的 |
|---|---|---|
| 自我复审 | 自己 vs.自己 | 用同伴复审的标准来要求自己。不一定最有效,因为开发者对自己总是过于自信。如果能持之以恒,则对个人有很大好处 |
| 同伴复审 | 复审者 vs.开发者 | 简便易行,软件工程中最基本的复审手段 |
| 团队复审 | 团队 vs.开发者 | 有比较严格的规定和流程,适用于关键的代码,以及复审后不再更新的代码覆盖率高一有很多双眼睛盯着程序,但效率可能不高( 全体人员都要到会) |
- 结对编程
在结对编程模式下,一对程序员肩并肩、平等地、互补地进行开发工作。他们并排坐在一台电脑前,面对同一个显示器,使用同一个键盘、同一个鼠标一起工作。他们一起分析,一起设计,一起写测试用例,一起编码,一起做单元测试,一起做集成测试,一起写文档等。- 结对编程的角色:
- 驾驶员( Driver) :控制键盘输人。
- 领航员(Navigator) :起到领航、提醒的作用。
- 结对编程的好处
- 在开发层次,结对编程能提供更好的设计质量和代码质量,两人合作解决问题的能力更强。两人合作,还有相互激励的作用,工程师看到别人的思路和技能,得到实时的讲解,受到激励,从而努力提高自己的水平,提出更多创意。
- 对开发人员自身来说,结对工作能带来更多的信心,高质量的产出能带来更高的满足感。
- 在企业管理层次上,结对能更有效地交流,相互学习和传递经验,分享知识,能更好地应对人员流动。
- 结对编程的角色:
任务2:两两自由结对,对结对方《实验二 软件工程个人项目》的项目成果进行评价#
- 对项目博文作业进行阅读并进行评论
| 评论博客链接 | 评论内容 |
|---|---|
| 201971010116-姜婷 实验二 0/1背包 | 1. 博文结构:整体结构精练,排版也比较好,特别是有目录,查看非常方便。 2. 博文内容:正文内容基本完成了要求的实验内容,从不同的方面描述了此次实验项目,但对于项目的核心技术部分可以再深入研究并写在博客中,会更好一点。博主也可考虑将项目代码以模块化的方式,根据不同的功能模块对代码进行划分。 3. 博文结构与PSP中“任务内容”列的关系:博主在博客中所写到的项目实现流程基本与PSP的主要流程一致,可见博主是按照PSP来完成此次项目的,博客正文结构简单明了,逻辑性较好。 4. PSP中“计划共完成需要的时间”与“实际完成需要的时间”两列数据的差异化分析与原因探究:博主在PSP中的实际完成需要的时间数据比计划完成需要的时间较长,对实际问题所需时间的把控不太好,项目开发编码阶段所需时间较长,可能是编程方面有一定的阻力,博主可多多练习编程。 |
- 克隆结对方项目源码到本地机器,阅读并测试运行代码,参照核查表复审同伴项目代码并记录。
- 已成功克隆结对方项目源码到本地文件夹
- 已阅读并测试运行代码
选择数据集2,采用动态规划算法解决0-1问题,所求解为388,运行时间也已给出,该项目也实现了对求解结果的保存,具体如下图所示:
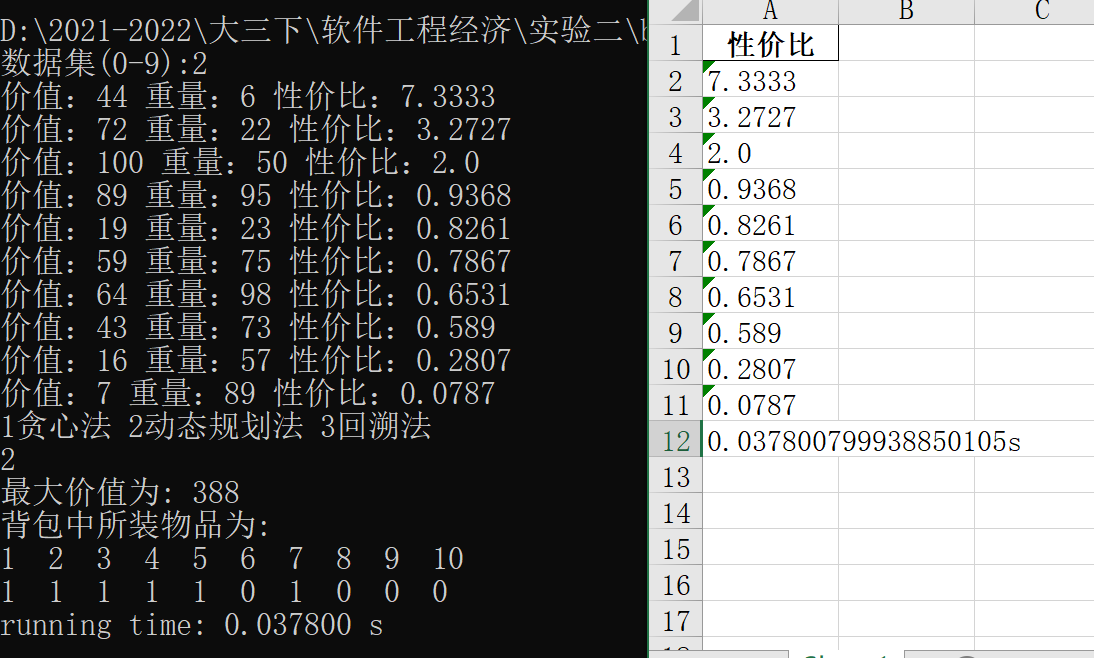
利用0-1背包测试数据绘制散点图的功能也以实现,如下图所示为利用数据集2绘制散点图:
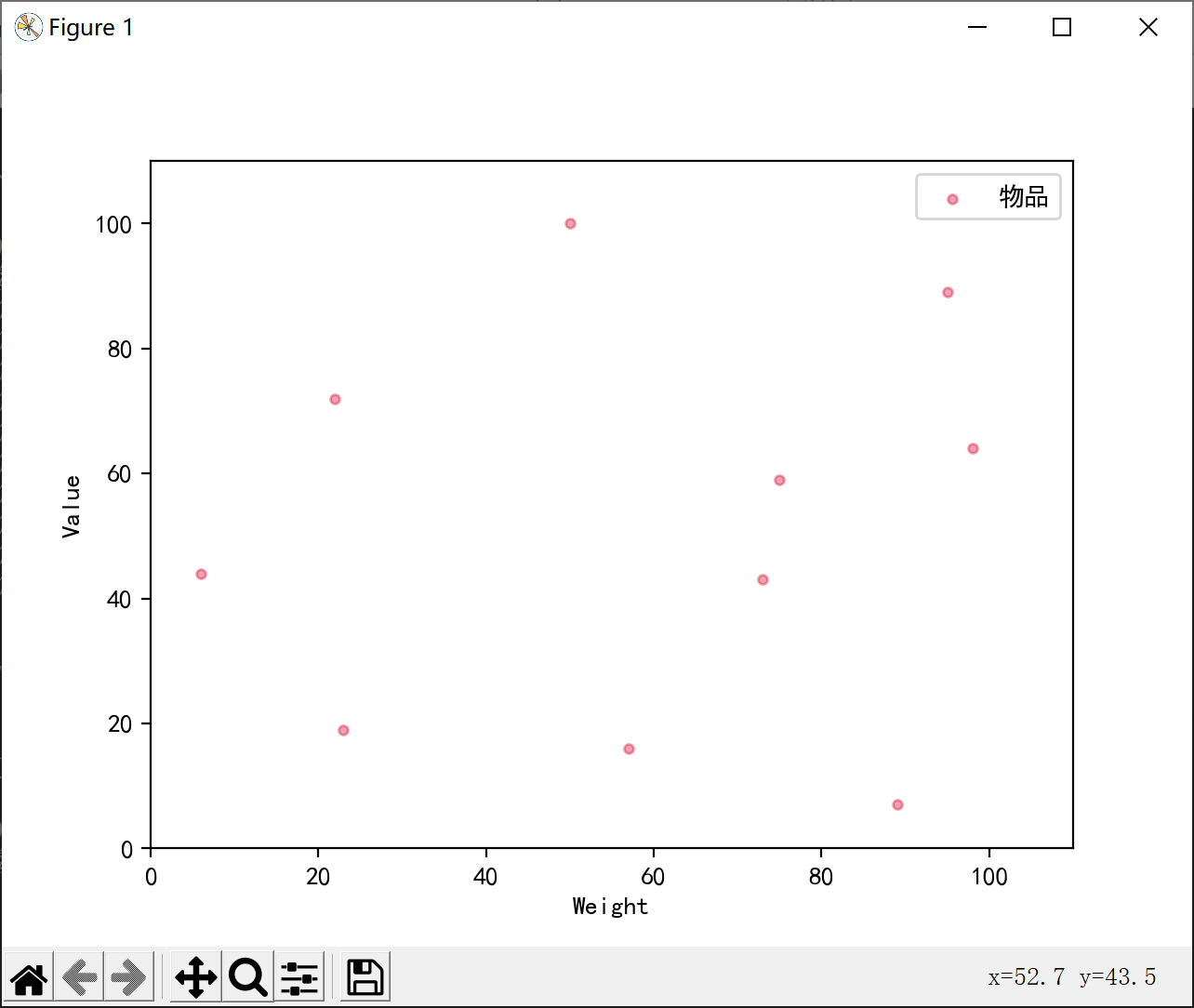
| 项目 | 内容 |
|---|---|
| 概要部分 | |
| 代码符合需求和规格说明么? | 符合需求和规格说明,基本实现了全部功能 |
| 代码设计是否考虑周全? | 基本考虑了所有需求设计功能 |
| 代码可读性如何? | 对关键代码进行了注释,可读性较好 |
| 代码容易维护么? | 不太容易维护,整体代码以一个模块展示,对于不同功能进行修改时,可能对其他代码有影响 |
| 代码的每一行都执行并检查过了吗? | 对项目代码都已执行并检查过 |
| 设计规范部分 | |
| 设计是否遵从已知的设计模式或项目中常用的模式? | 项目设计遵守 |
| 有没有硬编码或字符串/数字等存在? | 有 |
| 代码有没有依赖于某一平台,是否会影响将来的移植? | 移植影响较小 |
| 开发者新写的代码是否用已有的Library/SDK/Framework中的功能实现?在本项目中是否存在类似的功能可以通过调用而不用全部重新实现? | 未用到 |
| 有没有无用的代码可以清除? | 有 |
| 代码规范部分 | |
| 修改的部分符合代码标准和风格么? | 基本符合 |
| 具体代码部分 | |
| 有没有对错误进行处理?对于调用的外部函数,是否检查了返回值或处理了异常? | 已处理所出现错误 |
| 参数传递有无错误,字符串的长度是字节的长度还是字符的长度,是从0开始计数还是从1开始计数 | 无错误出现;字符的长度;从0开始 |
| 边界条件是如何处理的?switch语句和default分支是如何处理的?循环有没有可能出现死循环? | 前提分析推导边界条件;可能 |
| 有没有使用断言来保证我们认为不变的条件真的得到满足? | 否 |
| 对资源的利用,是在哪里申请,在哪里释放的?有无可能存在资源泄露?有没有优化的空间? | 使用程序语句进行申请、释放;不存在资源泄露;有优化空间 |
| 数据结构中有没有用不到的元素? | 无 |
| 效能 | |
| 代码的效能如何?最坏的情况是怎么样的? | 效能较好;最坏情况下算法无法得出正确解 |
| 代码中,特别是循环中是否有明显可优化的部分? | 无,目前未找到 |
| 对于系统和网络的调用是否会超时?如何处理? | 不会超时 |
| 可读性 | |
| 代码可读性如何?有没有足够的注释? | 对关键代码均有注释,可读性较好 |
| 可测试性 | |
| 代码是否需要更新或创建新的单元测试? | 需要 |
- 依据复审结果尝试利用github的Fork、Clone、Push、Pull request、Merge pull request等操作对同伴个人项目仓库的源码进行合作修改。
- Clone操作:拷贝项目仓库到本地文件夹
- Fork操作:将项目代码克隆到自己的仓库
任务3:采用两人结对编程方式,设计开发一款{0-1}KP 实例数据集算法实验平台,使之具有以下功能:#
1. 需求分析#
- Who 为谁设计,用户是谁?
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景,出现在各种领域的现实世界的决策过程中,主要用户为在决策过程中,如寻找最少浪费的方式来削减原材料,选择投资和投资组合,选择资产支持资产证券化,和生成密钥为Merkle-Hellman 和其他背包密码系统等方面所遇到问题的人。 - What 需要解决如下问题?
- 正确存储并读取数据
将{0-1}KP 实例数据集存储在mysql数据库中,使用数据时从数据库读取实验数据文件的有效{0-1}KP数据; - 排序
对任意一组{0-1}KP数据按重量比进行非递增排序 - 算法求解
用户自主选择贪心算法、动态规划算法、回溯算法,遗传算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位) - 保存结果
将任意一组{0-1} KP数据的最优解、和解向量可保存为Excel表格 - 保存日志数据
可动态嵌入任何一个有效的{0-1}KP 实例求解算法,并保存算法实验日志数据 - 实现人机交互界面为GUI界面
通过Android Studio 构建APP框架的方式和web页面访问的方式实现人机交互界面 - 绘制散点图
对任意一组{0-1}KP数据绘制以重量为横轴、价值为纵轴的数据散点图 - 绘制条形图(扩展部分)
对任意一组{0-1}KP数据绘制以重量为横轴、价值为纵轴的数据条形图 - 实现用户的登录注册(扩展部分)
用户可通过注册账号,使用账号密码登录成功后即可使用app
- 正确存储并读取数据
- Why 为什么解决这些问题?
通过查阅资料,学习不同的算法去解决0-1背包问题,提高自己的编程能力,学习软件项目的开发和管理
2. 软件功能设计#
该项目开发过程中主要实现了11个功能,具体功能设计如下图所示:
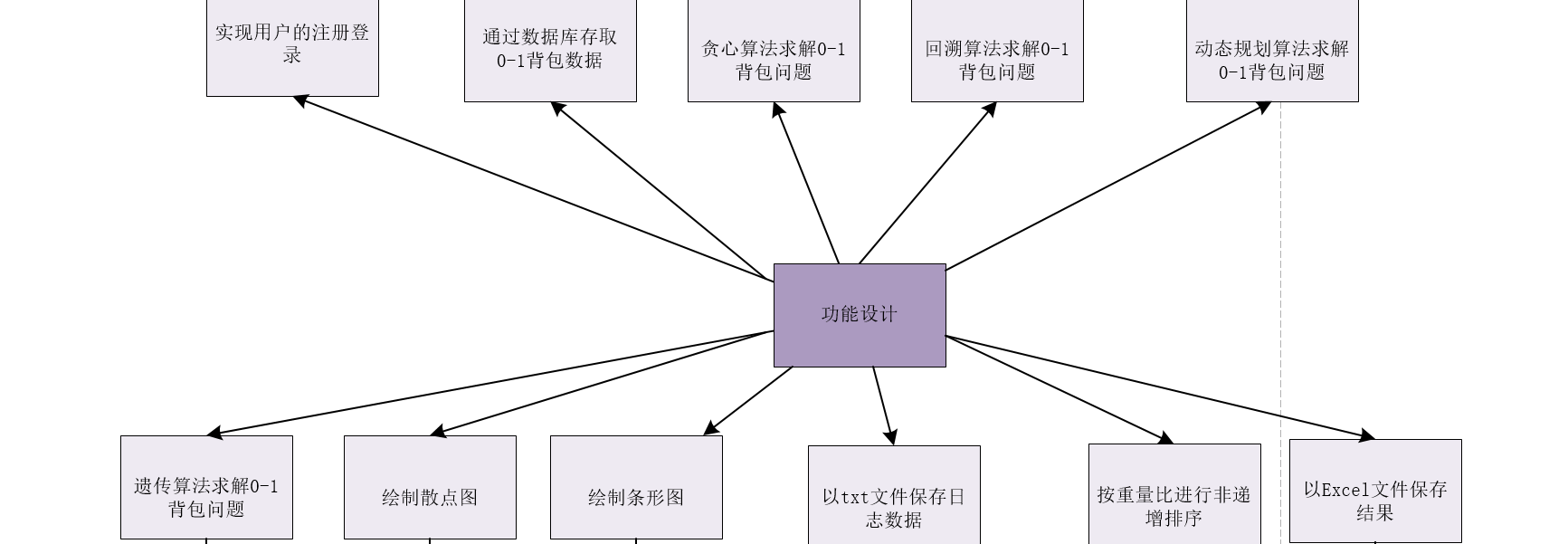
成员分工如下表所示:
| 成员 | 负责内容 |
|---|---|
| 201971010259_张圆圆 | app界面的搭建及逻辑实现 |
| 201971010116_姜婷 | web界面的搭建及逻辑实现 |
3.APP实现及核心功能展示#
整体项目结构及关系介绍#
在此次项目开发过程中,前端页面实现所用的文件如下所示:
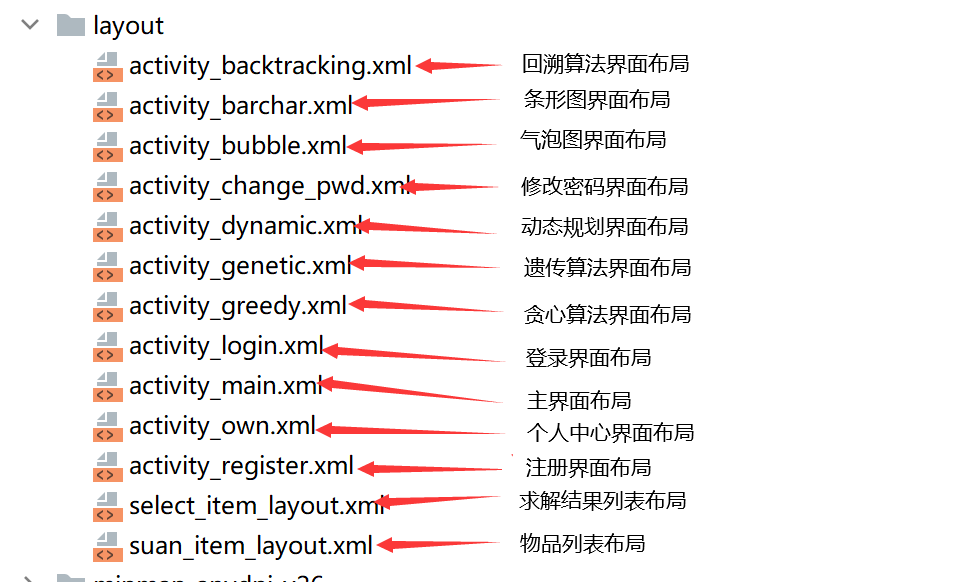
后端数据库及页面逻辑功能实现项目结构介绍如下图所示:
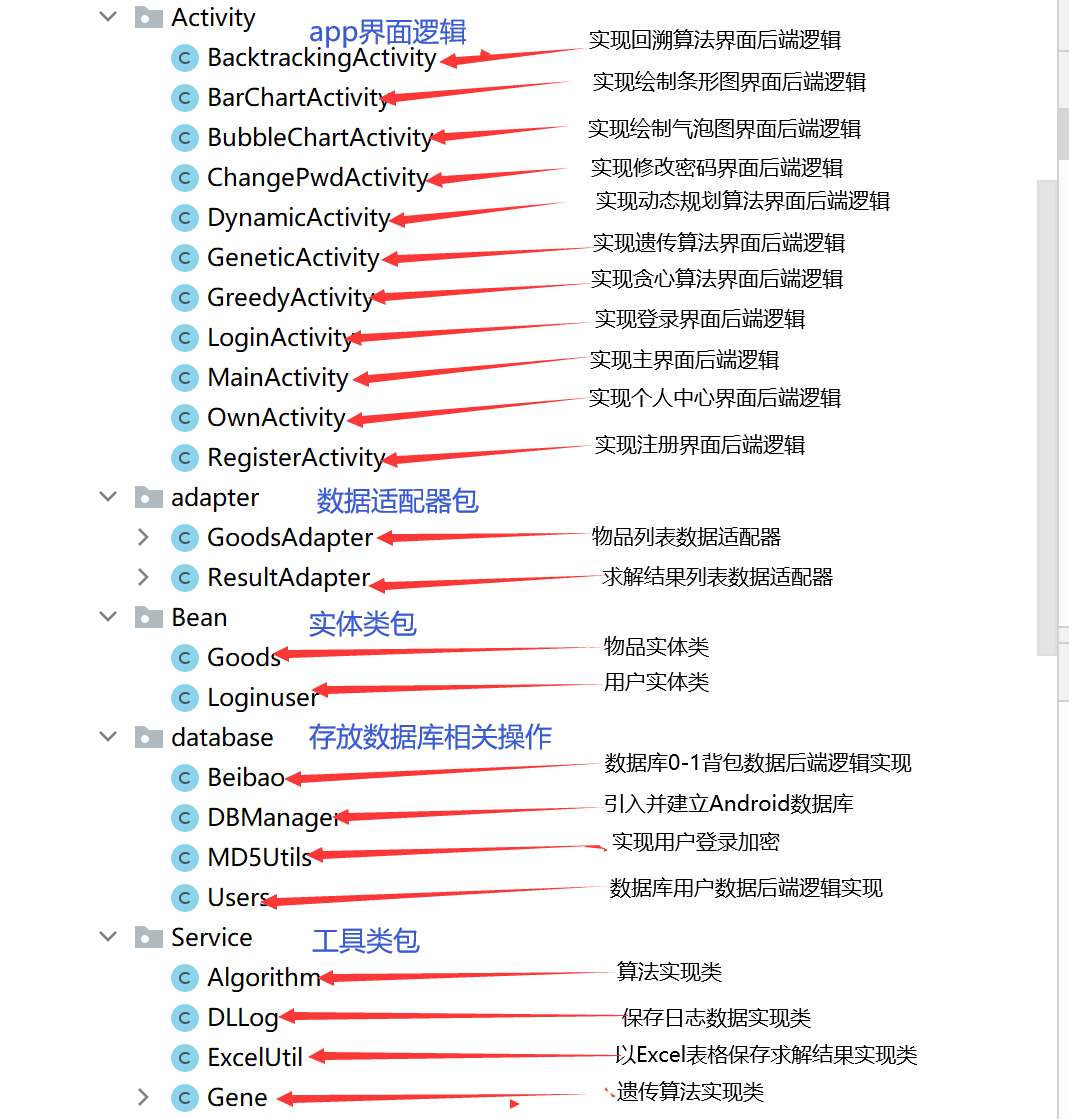
此项目所用到数据库具体如下图所示:
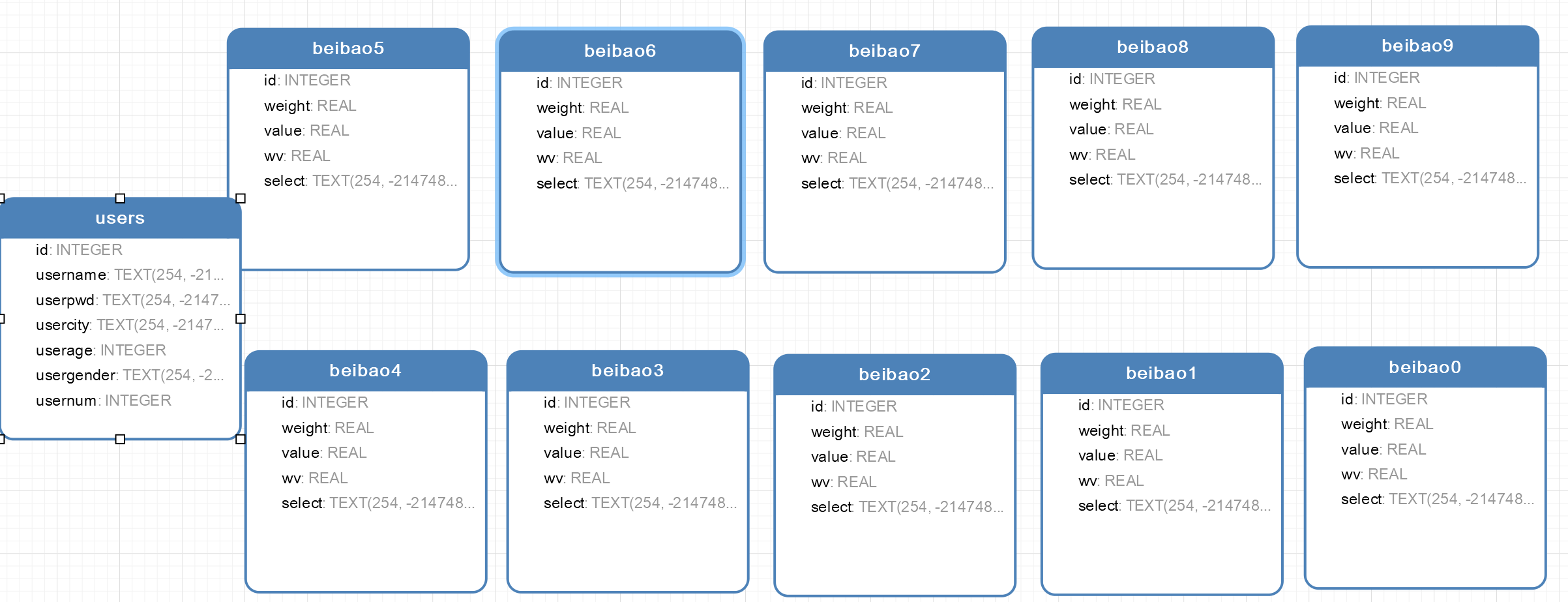
此次项目中,前端页面,数据库及后端逻辑功能实现之间的关系如下图所示:
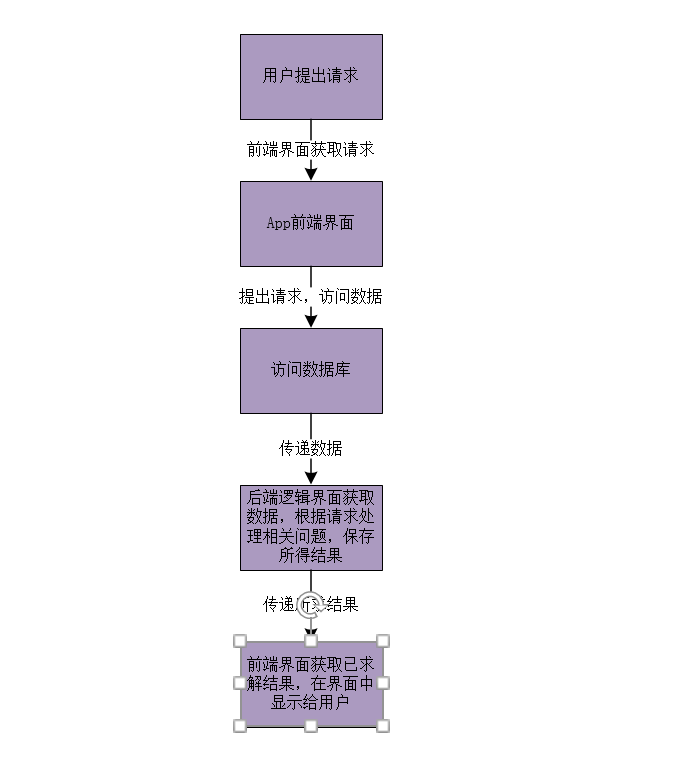
4. 核心类及函数介绍#
-
引入数据库
每个应用程序都要使用数据,Android应用程序也不例外,Android使用开源的、与操作系统无关的SQL数据库—SQLite。SQLite是一款轻量级数据库,它的设计目标是嵌入式的,占用资源非常的低,已经被多种软件和产品使用,Android使用SQLite来存储数据的。本项目中主要通过DBManager类来实现将外部数据库Knapsack引入app中,并将其存放在该app的database包中,核心代码如下所示:public static final String DB_NAME = "knapsacks.db"; //保存的数据库文件名 public static final String PACKAGE_NAME = "com.example.knapsack";//包名 public static final String DB_PATH = "/data" + Environment.getDataDirectory().getAbsolutePath() + "/" + PACKAGE_NAME + "/databases"; //存放数据库的位置 private SQLiteDatabase database; private Context context; public DBManager(Context context) { this.context = context; } public void openDatabase() { File dFile = new File(DB_PATH);//判断路径是否存在,不存在则创建路径 if (!dFile.exists()) dFile.mkdir(); this.database = this.openDatabase(DB_PATH + "/" + DB_NAME); } private SQLiteDatabase openDatabase(String dbfile) { try { if (!(new File(dbfile).exists())) { //打开数据库文件 InputStream is = this.context.getResources().getAssets().open("Knapsack.db"); //欲导入的数据库 FileOutputStream fos = new FileOutputStream(dbfile); int BUFFER_SIZE = 1028 * 10; byte[] buffer = new byte[BUFFER_SIZE]; int count = 0; while ((count = is.read(buffer)) > 0) { fos.write(buffer, 0, count); } fos.close(); is.close(); } return SQLiteDatabase.openOrCreateDatabase(dbfile, null); } catch (FileNotFoundException e) { Log.e("Database", "File not found"); e.printStackTrace(); } catch (IOException e) { Log.e("Database", "IO exception"); e.printStackTrace(); } return null; } -
用户登录采用MD5加密方式
MD5算法具有以下特点:
1、压缩性:任意长度的数据,算出的MD5值长度都是固定的。
2、容易计算:从原数据计算出MD5值很容易。
3、抗修改性:对原数据进行任何改动,哪怕只修改1个字节,所得到的MD5值都有很大区别。
4、强抗碰撞:已知原数据和其MD5值,想找到一个具有相同MD5值的数据(即伪造数据)是非常困难的。
5、不可逆(作者自己加的):已知原数据的MD5值,无法算出原数据。
MD5的作用是让大容量信息在用数字签名软件签署私人密钥前被"压缩"成一种保密的格式(就是把一个任意长度的字节串变换成一定长的十六进制数字串),以此来保护信息安全。在实现用户登录时,本项目选用了MD5加密方式,具体代码如下所示:
点击查看代码
/**
* md5加密方法
* @param password
* @return
*/
public static String md5Password(String password){
try {//得到一个信息摘要器
MessageDigest digest = MessageDigest.getInstance("md5");
byte[] result = digest.digest(password.getBytes());
StringBuffer buffer = new StringBuffer();//要把每一个byte做一个与运算0xff,0xff是十六进制,十进制为255
for(byte b:result){//与运算
int number = b & 0xff;
String str = Integer.toHexString(number);
//如果位数不够前面加个零
if(str.length()==1){
buffer.append("0");
}
buffer.append(str);
}
//标准的md5加密后的结果
return buffer.toString();
} catch (NoSuchAlgorithmException e) {
// TODO Auto-generated catch block
e.printStackTrace();
return "";
}
}
- 贪心算法-函数Greedy( )
- 为了求解该背包问题,我们首先计算每个商品的单位重量价值比(v/w),将物品按照其单位重量价值比来进行排序,遵循贪心策略,首先尽量多地拿走单位重量价值比最高的商品,如果该商品已全部拿走而背包未装满,则继续尽量多地拿走单位重量价值比第二高的商品,依次类推,直到达到重量上限W,背包已无法容纳其他物品,则可得到解,但所得解不是最优解,因为它无法保证最终能将背包装满,部分闲置的背包空间使每公斤背包空间的价值降低了,其算法流程图如下所示:
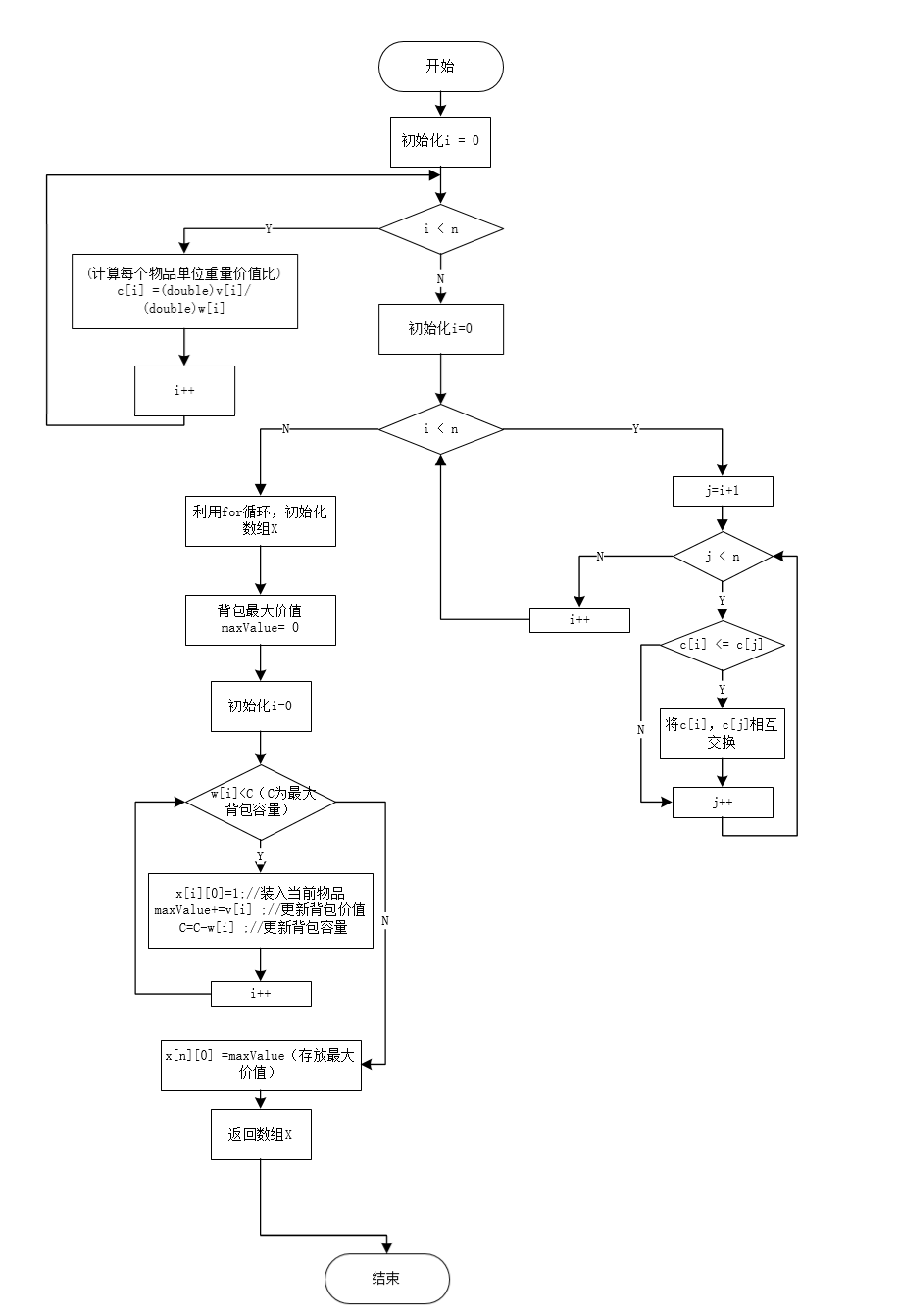
- 贪心算法核心代码
点击查看代码
//贪心算法
public List<Goods> Greedy(List<Goods> list)
{
int C = list.get(0).getWeight();
int n = (int)list.get(0).getValue();
//计算每个物品单位重量价值比,对每个物品按照单位重量价值比进行排序
knapsack(list);
//初始化数组x
for(int i = 1;i <= n;i++)
{
list.get(i).setSelect("No");
}
int maxValue= 0;//背包最大价值
for (int i=1; list.get(i).getWeight()<C; i++ )
{
list.get(i).setSelect("Yes");//装入当前物品
maxValue+=list.get(i).getValue() ;//更新背包价值
C=C-list.get(i).getWeight() ;//更新背包容量
}
list.get(0).setSelect(maxValue+"");
for(int i=1;i<=n-1;i++)
{
for(int j=i+1;j<=n;j++)
if(list.get(i).getId()>list.get(j).getId())//冒泡排序
{
swap(list,i,j);
}
}
return list;
}
- 回溯算法-函数backtrack( )
- 利用回溯法解决0-1背包,属于找最优解问题,需要构造解的子集树。对于每一个物品i,对于该物品只有选与不选2个决策,若总共有n个物品,可以顺序依次考虑每个物品,这样就形成了一棵解空间树, 遍历这棵树,以枚举所有情况。为了更好地计算,首先利用函数knapsack()先将物品按照其单位重量价值从大到小排序,然后再进行遍历搜索。在搜索状态空间树时,只要左子节点是可一个可行结点,搜索就进入其左子树。对于右子树时,先计算上界函数,以判断是否将其减去(剪枝),最后进行判断,如果重量不超过背包容量,且价值最大的话,该方案就是最后的答案,其中构造了上界函数bound():当前价值cw+剩余容量可容纳的最大价值<=当前最优价值bestp,利用其进行剪枝,其算法流程图如下所示:

- 回溯算法核心代码
点击查看代码
double cw = 0.0;//当前背包重量
double cp = 0.0;//当前背包中物品价值
double bestp = 0.0;//当前最优价值
//回溯函数
void backtrack(int i,List<Goods> list)
{
int C = list.get(0).getWeight();
int n = (int)list.get(0).getValue();
bound(i,list); //计算上界
if(i>n) //所有元素都已遍历到,回溯结束
{
bestp = cp;
return ;
}
if(cw+list.get(i).getWeight()<=C)
{
//放入背包
cw+=list.get(i).getWeight();
cp+=list.get(i).getValue();
list.get(i).setSelect("Yes");
backtrack(i+1,list);
cw-=list.get(i).getWeight();
cp-=list.get(i).getValue();
}
if(bound(i+1,list)>bestp)//符合条件搜索右子数
backtrack(i+1,list);
}
//计算上界函数
double bound(int i ,List<Goods> list)
{
int C = list.get(0).getWeight();
int n = (int)list.get(0).getValue();
double leftw= C-cw;
double b = cp;
while(i<= n && list.get(i).getWeight()<=leftw)
{
leftw-=list.get(i).getWeight();
b+=list.get(i).getValue();
i++;
}
if(i<=n)
b+=list.get(i).getValue()/list.get(i).getWeight()*leftw;
return b;//返回上界值
}
private static <E> void swap(List<E> list,int index1,int index2) {
//定义第三方变量
E e=list.get(index1);
//交换值
list.set(index1, list.get(index2));
list.set(index2, e);
}
//按单位价值排序
void knapsack(List<Goods> list)
{
int i,j;
int temp = 0;
int C = list.get(0).getWeight();
int n = (int)list.get(0).getValue();
for( i = 1;i <= n;i++)
{
Goods g = list.get(i);
double d = g.getValue()/g.getWeight();
// d = new BigDecimal(d.setScale(2, BigDecimal.ROUND_HALF_UP).doubleValue()
g.setWvproportion( d);
list.get(i).setWvproportion(g.getWvproportion());
list.get(i).setSelect("No");
}
for(i=1;i<=n-1;i++)
{
for(j=i+1;j<=n;j++)
if(list.get(i).getWvproportion()<list.get(j).getWvproportion())//冒泡排序
{
swap(list,i,j);
}
}
}
public List<Goods> Backtracking(List<Goods> list)
{
knapsack(list);
backtrack(1,list);
list.get(0).setSelect(bestp+"");
int n = (int)list.get(0).getValue();
for(int i=1;i<=n-1;i++)
{
for(int j=i+1;j<=n;j++)
if(list.get(i).getId()>list.get(j).getId())//冒泡排序
{
swap(list,i,j);
}
}
return list;
}
- 动态规划算法-函数Dynamic( )
- 利用动态规划算法求解0-1背包问题时,在选择装入背包的物品时,对每种物品i只有两种选择:装入背包或不装入背包。在0/1背包问题中,其动态规划函数为:
V(i,j)表示把前i个物品放入容量为j的背包中的最大价值和,根据上述分析,设n个物品的重量存储在数组w[n]中,价值存储在数组v[n]中,背包容量为C,数组V[n+1][C+1]存放迭代结果,其中V[i][j]表示前i个物品装入容量为j的背包中获得的最大价值,数组x[n]存储装入背包的物品。其算法流程图如下所示:
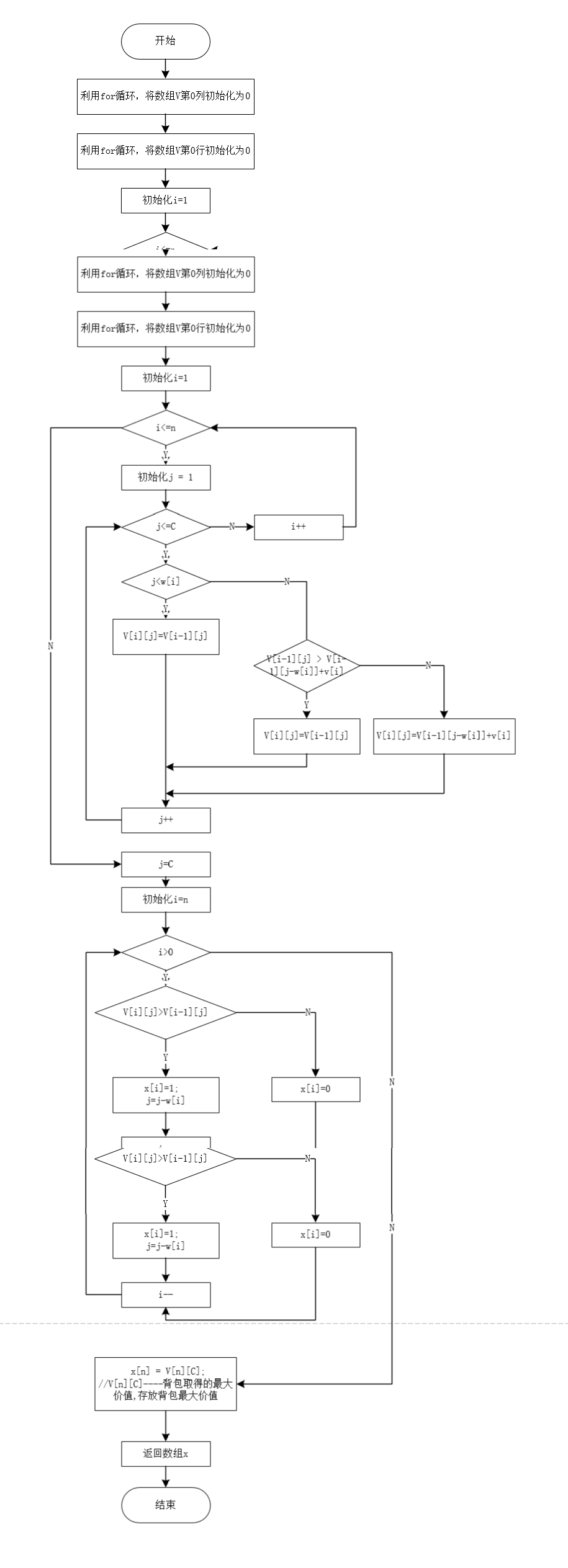
- 动态规划算法核心代码
点击查看代码
//动态规划算法
public List<Goods> Dynamic(List<Goods> list)
{
int i,j;
int C = list.get(0).getWeight();
int n = (int)list.get(0).getValue();
int[][] V = new int [10000][10000];
for (i=0; i<=n; i++) //初始化第0列
{
V[i][0]=0;
}
for (j=0; j<=C; j++) //初始化第0行
{
V[0][j]=0;
}
for (i=1; i<=n; i++) //计算第i行,进行第i次迭代
{
for (j=1; j<=C; j++)
{
if (j<list.get(i).getWeight())
{
V[i][j]=V[i-1][j];
}
else
{
if(V[i-1][j] > V[i-1][j-list.get(i).getWeight()]+list.get(i).getValue())
{
V[i][j]=V[i-1][j];
}
else
{
V[i][j]= (int) (V[i-1][j-list.get(i).getWeight()]+list.get(i).getValue());
}
}
}
}
j=C; //求装入背包的物品
for (i=n; i>0; i--)
{
if (V[i][j]>V[i-1][j])
{
list.get(i).setSelect("Yes");
j=j-list.get(i).getWeight();
}
else
{
list.get(i).setSelect("No");
}
}
list.get(0).setSelect(V[n][C]+"");//V[n][C]----背包取得的最大价值
for( i=1;i<=n-1;i++)
{
for( j=i+1;j<=n;j++)
if(list.get(i).getId()>list.get(j).getId())//冒泡排序
{
swap(list,i,j);
}
}
return list;
}
- 遗传算法
-
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。遗传算法有着鲜明的优点:
(1)遗传算法的操作对象是一组可行解,而非单个可行解;搜索轨道有多条,而非单条,因而具有良好的并行性.
(2)遗传算法只需利用目标的取值信息,而无需递度等高价值信息,因而适用于任何规模,高度非线形的不连续多峰函数的优化以及无解析表达式的目标函数的优化,具有很强的通用性.
(3)遗传算法择优机制是一种“软”选择,加上良好的并行性,使它具有良好的全局优化性和稳健性.
(4)遗传算法操作的可行解集是经过编码化的(通常采用二进制编码),目标函数解释为编码化个体(可行解)的适应值,因而具有良好的可操作性与简单性. -
在遗传算法中,所涉及到的状态表示如下所示:
(1)个体或染色体:问题的一个解,表示为n个比特的字符串,比特值为0表示不选该物品,比特值为1表示选择该物品。
(2)基因:染色体的每一个比特。
(3)种群:解的集合。
(4)适应度:衡量个体优劣的函数值。 -
在遗传算法中,所涉及到的控制参数如下所示:
(1)种群规模:解的个数。
(2)最大遗传的代数
(3)交叉率:参加交叉运算的染色体个数占全体染色体的比例,取值范围一般为0.4~0.99。
(4)变异率:发生变异的基因位数所占全体染色体的基因总位数的比例,取值范围一般为0.0001~0.1。 -
遗传算法描述
(1)在搜索空间上定义一个适应度函数,给定种群规模,交叉率和变异率,代数;
(2)随机产生搜索空间中的N个个体s1, s2, …, sN,组成初始种群S={s1, s2, …, sN},置代数计数器t=1;
(3)计算初始种群中每个个体的适应度f() ;
(4)若终止条件满足,则取初始种群中适应度最大的个体作为所求结果,算法结束。
(5)按选择概率所决定的选中机会,每次从初始种群中随机选定1个个体并将其染色体复制,共做N次,然后将复制所得的N个染色体组成群体S1;
(6)按交叉率所决定的参加交叉的染色体数c,从S1中随机确定c个染色体,配对进行交叉操作,并用产生的新染色体代替原染色体,得群体S2;
(7)按变异率所决定的变异次数m,从S2中随机确定m个染色体,分别进行变异操作,并用产生的新染色体代替原染色体,得群体S3;
(8)将群体S3作为新一代种群,即用S3代替初始种群,令t = t+1,转步3。 -
遗传算法核心代码
-
//初始化初始种群
private void initPopulation() {
fitness = new float[scale];
population = new boolean[scale][len];
//考虑到随机生成的初始化种群效果有可能不好,这里对于种群的初始化作了一定的优化
//对于每一个个体,先随机一个容量值(0.5 capacity 至 1.5 capacity)
//然后随机相应的物品到该个体中,直到超过上面随机的容量
for(int i = 0; i < scale; i++) {
float tmp = (float)(0.5 + Math.random()) * capacity;
int count = 0; //防止初始化耗费太多计算资源
for(int j = 0; j < tmp;) {
int k = random.nextInt(len);
if(population[i][k]) {
if(count == 3) {
break;
}
count++;
continue;
} else {
population[i][k] = true;
j += weight[k];
count = 0;
}
}
}
}
//计算一个个体的适应度
private float evaluate(boolean[] unit) {
float profitSum = 0;
float weightSum = 0;
for (int i = 0; i < unit.length; i++) {
if (unit[i]) {
weightSum += weight[i];
profitSum += profit[i];
}
}
if (weightSum > capacity) {
//该个体的对应的所有物品的重量超过了背包的容量
return 0;
} else {
return profitSum;
}
}
//计算种群所有个体的适应度
private void calcFitness() {
for(int i = 0; i < scale; i++) {
fitness[i] = evaluate(population[i]);
}
}
//记录最优个体
private void recBest(int gen) {
for(int i = 0; i < scale; i++) {
if(fitness[i] > bestFitness) {
bestFitness = fitness[i];
bestUnit = new boolean[len];
for(int j = 0; j < len; j++) {
bestUnit[j] = population[i][j];
}
}
}
}
//种群个体选择
//选择策略:适应度前10%的个体带到下一次循环中,然后在(随机生成10%的个体 + 剩下的90%个体)中随机取90%出来
private void select() {
SortFitness[] sortFitness = new SortFitness[scale];
for(int i = 0; i < scale; i++) {
sortFitness[i] = new SortFitness();
sortFitness[i].index = i;
sortFitness[i].fitness = fitness[i];
}
Arrays.sort(sortFitness);
boolean[][] tmpPopulation = new boolean[scale][len];
//保留前10%的个体
int reserve = (int)(scale * 0.1);
for(int i = 0; i < reserve; i++) {
for(int j = 0; j < len; j++) {
tmpPopulation[i][j] = population[sortFitness[i].index][j];
}
//将加入后的个体随机化
for(int j = 0; j < len; j++) {
population[sortFitness[i].index][j] = false;
}
float tmpc = (float)(0.5 + Math.random()) * capacity;
int count = 0;
for(int j = 0; j < tmpc;) {
int k = random.nextInt(len);
if(population[sortFitness[i].index][k]) {
if(count == 3) {
break;
}
count++;
continue;
} else {
population[sortFitness[i].index][k] = true;
j += weight[k];
count = 0;
}
}//
}
//再随机90%的个体出来
List<Integer> list = new ArrayList<Integer>();
for(int i = 0; i < scale; i++) {
list.add(i);
}
for(int i = reserve; i < scale; i++) {
int selectid = list.remove((int)(list.size()*Math.random()));
for(int j = 0; j < len; j++) {
tmpPopulation[i][j] = population[selectid][j];
}
}
population = tmpPopulation;
}
//进行交叉
private void intersect() {
for(int i = 0; i < scale; i = i + 2)
for(int j = 0; j < len; j++) {
if(Math.random() < irate) {
boolean tmp = population[i][j];
population[i][j] = population[i + 1][j];
population[i + 1][j] = tmp;
}
}
}
//变异
private void aberra() {
for(int i = 0; i < scale; i++) {
if(Math.random() > arate1) {
continue;
}
for(int j = 0; j < len; j++) {
if(Math.random() < arate2) {
population[i][j] = Math.random() > 0.5 ? true : false;
}
}
}
}
//遗传算法
public void solve() {
readDate();
initPopulation();
for(int i = 0; i < maxgen; i++) {
//计算种群适应度值
calcFitness();
//记录最优个体
recBest(i);
//进行种群选择
select();
//进行交叉
intersect();
//发生变异
aberra();
}
int totalWeight = 0;
for(int i = 0; i < bestUnit.length; i++) {
System.out.println("bestUnit.length:" + bestUnit.length);
System.out.println("goods:" + goods.size());
if(bestUnit[i]){
totalWeight += weight[i]; goods.get(i+1).setSelect("Yes");
}
}
goods.get(0).setSelect(bestFitness+"");
}
- 遗传算法流程图
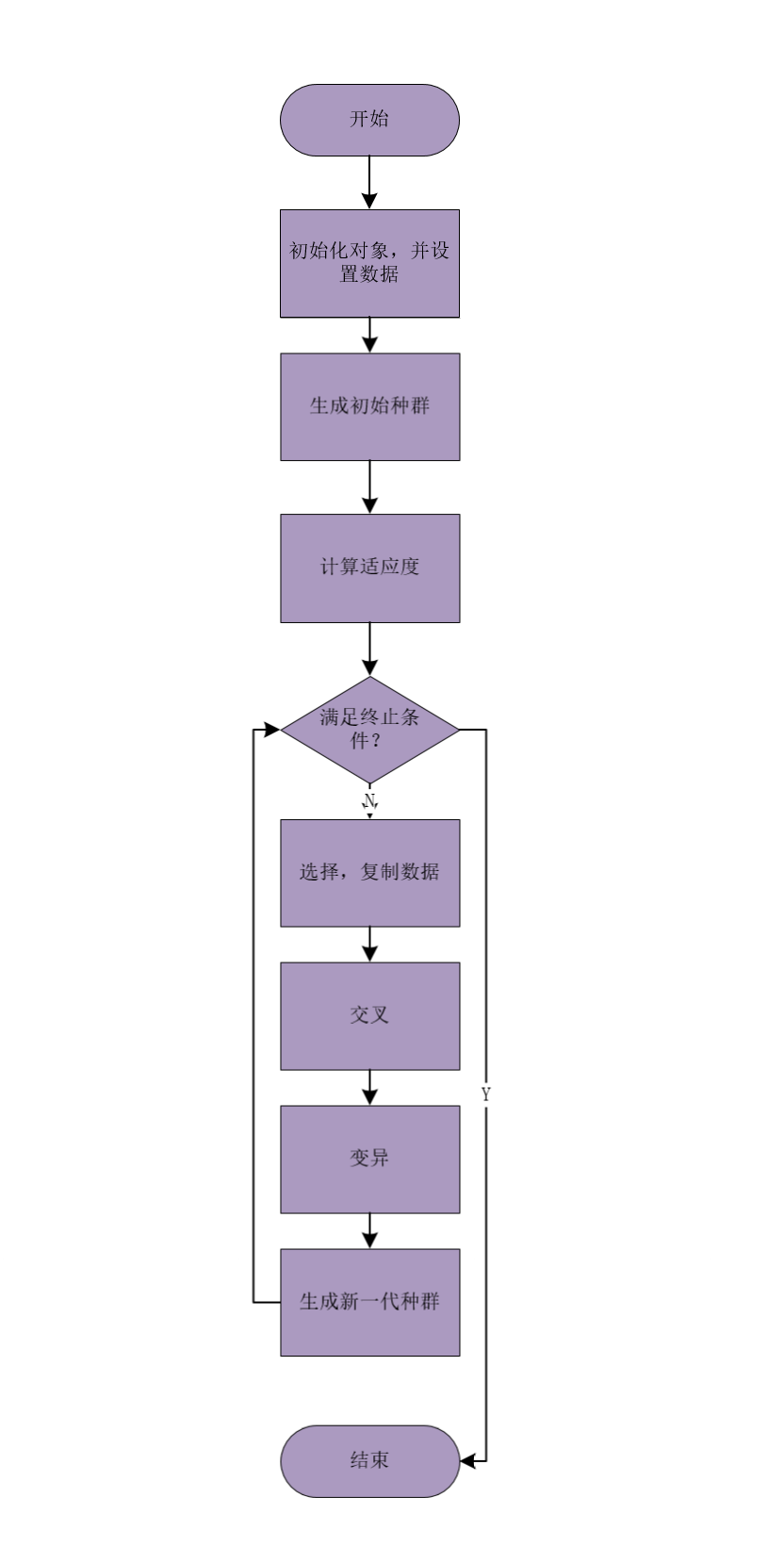
-
快速排序算法-函数quickSort()
-
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
(1) 首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2) 将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于分界值,而右边部分中各元素都大于或等于分界值。
(3) 然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4) 重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。 -
快速排序算法核心代码展示
点击查看代码
public static int partition(List<Goods> list,int left,int right){ int pivot = left; int id = list.get(pivot).getId(); int weight = list.get(pivot).getWeight(); double value = list.get(pivot).getValue(); double wv = list.get(pivot).getWvproportion(); while(left < right){ while(left<right && list.get(right).getWvproportion() > list.get(pivot).getWvproportion()) { right--; } list.get(left).setId(list.get(right).getId()); list.get(left).setWeight(list.get(right).getWeight()); list.get(left).setValue(list.get(right).getValue()); list.get(left).setWvproportion(list.get(right).getWvproportion()); while(left < right && list.get(left).getWvproportion() <= list.get(pivot).getWvproportion()) { left++; } list.get(right).setId(list.get(left).getId()); list.get(right).setWeight(list.get(left).getWeight()); list.get(right).setValue(list.get(left).getValue()); list.get(right).setWvproportion(list.get(left).getWvproportion()); } list.get(left).setId(id); list.get(left).setWeight(weight); list.get(left).setValue(value); list.get(left).setWvproportion(wv); return left; } public static List<Goods> quickSort(List<Goods> list,int left,int right){ int middle; if(left < right){ middle = partition(list,left,right); quickSort(list,left,middle-1); quickSort(list,middle+1,right); } return list; }
-
-
保存日志数据
在DLLog类中构造了向日志文件写入数据的函数方法writeLogtoFile(),在用户进行操作时,就会调用该方法,进行日志数据的写入,并将其数据以txt的方式存储下来,核心代码如下所示:/** * 打开日志文件并写入日志 * * @return * **/ private static void writeLogtoFile(String mylogtype, String tag, String text) { Date nowtime = new Date(); String needWriteFiel = logfile.format(nowtime); String needWriteMessage = LogSdf.format(nowtime) + " " + mylogtype + " " + tag + " " + text; File logdir = new File(LOG_PATH_SDCARD_DIR);// 如果没有log文件夹则新建该文件夹 if (!logdir.exists()) { logdir.mkdirs(); } File file = new File(LOG_PATH_SDCARD_DIR, needWriteFiel + LOGFILENAME); try { FileWriter filerWriter = new FileWriter(file, true);// 后面这个参数代表是不是要接上文件中原来的数据,不进行覆盖 BufferedWriter bufWriter = new BufferedWriter(filerWriter); bufWriter.write(needWriteMessage); bufWriter.newLine(); bufWriter.close(); filerWriter.close(); } catch (IOException e) { e.printStackTrace(); } } /** * 得到现在时间前的几天日期,用来得到需要删除的日志文件名 * */ private static Date getDateBefore() { Date nowtime = new Date(); Calendar now = Calendar.getInstance(); now.setTime(nowtime); now.set(Calendar.DATE, now.get(Calendar.DATE) - SDCARD_LOG_FILE_SAVE_DAYS); return now.getTime(); } -
保存求解结果(以Excel形式)
在用户选择不同的数据集及算法求解完成0-1背包问题后,点击界面的“保存结果”按钮,即可调用函数以Excel形式保存求解数据结果在文件夹/storage/self/primary/ExportExcel中,具体代码如下所示:/** * 将数据写入Excel表格 * * @param objList 要写的列表数据 * @param filePath 文件路径 * @param c 上下文 * @param <T> */ public static <T> void writeObjListToExcel(List<T> objList, String filePath, Context c) { if (objList != null && objList.size() > 0) { WritableWorkbook writebook = null; InputStream in = null; try { WorkbookSettings setEncode = new WorkbookSettings(); setEncode.setEncoding(UTF8_ENCODING); in = new FileInputStream(new File(filePath)); Workbook workbook = Workbook.getWorkbook(in); writebook = Workbook.createWorkbook(new File(filePath), workbook); WritableSheet sheet = writebook.getSheet(0); for (int j = 0; j < objList.size(); j++ ) { Goods goods = (Goods) objList.get(j); List<String> list = new ArrayList<>(); if(j == 0) { list.add(goods.getWeight() + "(背包总容量)"); list.add(goods.getValue() + "(物品数目)"); list.add(goods.getWvproportion() + ""); list.add(goods.getSelect() + "(背包最大价值)"); } else { list.add(goods.getWeight() + ""); list.add(goods.getValue() + ""); list.add(goods.getWvproportion() + ""); list.add(goods.getSelect() + ""); } for (int i = 0; i < list.size(); i++) { sheet.addCell(new Label(i, j + 1, list.get(i), arial12format)); if (list.get(i).length() <= 4) { //设置列宽 sheet.setColumnView(i, list.get(i).length() + 8); } else { //设置列宽 sheet.setColumnView(i, list.get(i).length() + 5); } } //设置行高 sheet.setRowView(j + 1, 350); } writebook.write(); Toast.makeText(c, " 导出成功 ", Toast.LENGTH_SHORT).show(); } catch (Exception e) { e.printStackTrace(); } finally { if (writebook != null) { try { writebook.close(); } catch (Exception e) { e.printStackTrace(); } } if (in != null) { try { in.close(); } catch (IOException e) { e.printStackTrace(); } } } } } -
利用MPAndroidChart绘制图像
MPAndroidChart是由一个来自澳大利亚的名叫Philipp Jahoda的大神所写,能画各种图表的一个库,在项目中引入该库,即可使用其进行绘图。MPAndroidChart支持线状图、柱状图、散点图、烛状图、气泡图、饼状图和蜘蛛网状图等,支持缩放、拖动(平移)、选择和动画等,在本项目利用 MPAndroidChart完成了气泡图和条形图的设置,具体代码展示如下所示:-
气泡图代码展示
点击查看代码
//起泡图 mBubbleChart = (BubbleChart) findViewById(R.id.mBubbleChart); mBubbleChart.getDescription().setEnabled(false); mBubbleChart.setOnChartValueSelectedListener(this); mBubbleChart.setDrawGridBackground(false); mBubbleChart.setTouchEnabled(true); mBubbleChart.setDragEnabled(true); mBubbleChart.setScaleEnabled(true); mBubbleChart.setMaxVisibleValueCount(200); mBubbleChart.setPinchZoom(true); Legend l = mBubbleChart.getLegend(); l.setVerticalAlignment(Legend.LegendVerticalAlignment.TOP); l.setHorizontalAlignment(Legend.LegendHorizontalAlignment.RIGHT); l.setOrientation(Legend.LegendOrientation.VERTICAL); l.setDrawInside(false); YAxis yl = mBubbleChart.getAxisLeft(); yl.setSpaceTop(20f); yl.setSpaceBottom(20f); yl.setDrawZeroLine(false); mBubbleChart.getAxisRight().setEnabled(false); XAxis xl = mBubbleChart.getXAxis(); xl.setPosition(XAxis.XAxisPosition.BOTTOM); -
条形图代码展示
-
//条形图
mBarChart = (BarChart) findViewById(R.id.mBarChart);
//设置表格上的点,被点击的时候,的回调函数
mBarChart.setOnChartValueSelectedListener(this);
mBarChart.setDrawBarShadow(false);
mBarChart.setDrawValueAboveBar(true);
mBarChart.getDescription().setEnabled(false);
// 如果60多个条目显示在图表,drawn没有值
mBarChart.setMaxVisibleValueCount(60);
// 扩展现在只能分别在x轴和y轴
mBarChart.setPinchZoom(false);
//是否显示表格颜色
mBarChart.setDrawGridBackground(false);
XAxis xAxis = mBarChart.getXAxis();
xAxis.setPosition(XAxis.XAxisPosition.BOTTOM);
xAxis.setDrawGridLines(false);
// 只有1天的时间间隔
xAxis.setGranularity(1f);
xAxis.setLabelCount(7);
xAxis.setAxisMaximum(120f);
xAxis.setAxisMinimum(0f);
YAxis leftAxis = mBarChart.getAxisLeft();
leftAxis.setLabelCount(8, false);
leftAxis.setPosition(YAxis.YAxisLabelPosition.OUTSIDE_CHART);
leftAxis.setSpaceTop(15f);
//这个替换setStartAtZero(true)
leftAxis.setAxisMinimum(0f);
leftAxis.setAxisMaximum(120f);
YAxis rightAxis = mBarChart.getAxisRight();
rightAxis.setDrawGridLines(false);
rightAxis.setLabelCount(8, false);
rightAxis.setSpaceTop(15f);
rightAxis.setAxisMinimum(0f);
rightAxis.setAxisMaximum(120f);
// 设置标示,就是那个一组y的value的
Legend l = mBarChart.getLegend();
l.setVerticalAlignment(Legend.LegendVerticalAlignment.BOTTOM);
l.setHorizontalAlignment(Legend.LegendHorizontalAlignment.LEFT);
l.setOrientation(Legend.LegendOrientation.HORIZONTAL);
l.setDrawInside(false);
//样式
l.setForm(Legend.LegendForm.SQUARE);
//字体
l.setFormSize(9f);
//大小
l.setTextSize(11f);
l.setXEntrySpace(50f);
5. 代码规范#
Java#
| 代码要求 | 代码规范 |
|---|---|
| 缩进 | * 缩进采用4个空格 * 第二行相对第一行缩进 4个空格,从第三行开始,不再继续缩进,参考示例。 * 运算符与下文一起换行。 * 方法调用的点符号与下文一起换行。 * 在多个参数超长,逗号后进行换行 |
| 变量命名 | * 标识符必须以字母或者下划线开头,其他可以是数字、字母、下划线 * 标识符中的字母不限大小写,但大小写意义不同 * 变量名长度不得超过最大长度限制 * 关键字不能作为变量名,变量命名时应尽量避开预定义变量 * 采取驼峰命名法,首字母小写,后续单词开头大写,专业术语缩写可全用大写 |
| 每行最多字符数 | 单行字符数限制不超过 120个,超出需要换 |
| 函数最大行数 | 75行,超过需要封装 |
| 函数、类命名 | 采用驼峰命名法,首字母需大写 |
| 常量 | 常量定义需要全部大写 |
| 空行规则 | 一句代码一行,函数与其他代码之间不空行 |
| 注释规则 | 单行注释不换行,多行注释需换行 |
| 操作符前后空格 | 无需空格 |
| 其他规则 | * 大括号。左大括号不另起一行,右大括号单独占一行。 * 循环语句里的变量。一般变量设置为i,若有嵌套循环则依次使用i、j、m、n。 |
Python#
- 文件声明
在文件开头声明文件编码,以下两种均可
# -*- coding: utf-8 -*-
# coding = utf-8
-
缩进规则
- 统一使用 4 个空格进行缩进,不要用tab, 更不要tab和空格混用
-
注释部分
- “#”号后面要空一格
-
空行
- 双空行:编码格式声明、模块导入、常量和全局变量声明、顶级定义(类的定义)和执行代码之间空两行
- 单空行:方法定义之间空一行,方法内分隔某些功能的位置也可以空一行
-
模块导入部分
- 导入应该放在文件顶部,位于模块注释和文档字符串之后,模块全局变量和常量之前。
- 导入应该照从最通用到最不通用的顺序分组,分组之间空一行,依次为:标准库导入-》第三方库导入-》应用程序指定导入
- 每个 import 语句只导入一个模块,尽量避免一次导入多个模块
-
Python命名建议遵循的一般性原则:
- 模块尽量使用小写命名,首字母保持小写,尽量不要用下划线
- 类名使用驼峰(CamelCase)命名风格,首字母大写,私有类可用一个下划线开头
- 函数名、变量名一律小写,如有多个单词,用下划线隔开,私有函数用一个下划线开头
- 常量采用全大写,如有多个单词,使用下划线隔开
-
引号
- 输出语句中使用单双引号都是可以正确的,此外 正则表达式推荐使用双引号、文档字符串 (docstring) 推荐使用三个双引号
6. 程序运行#
用户登录注册功能#
- (用户注册-APP界面)

- (用户登录--APP界面)

- (用户登录-web界面)
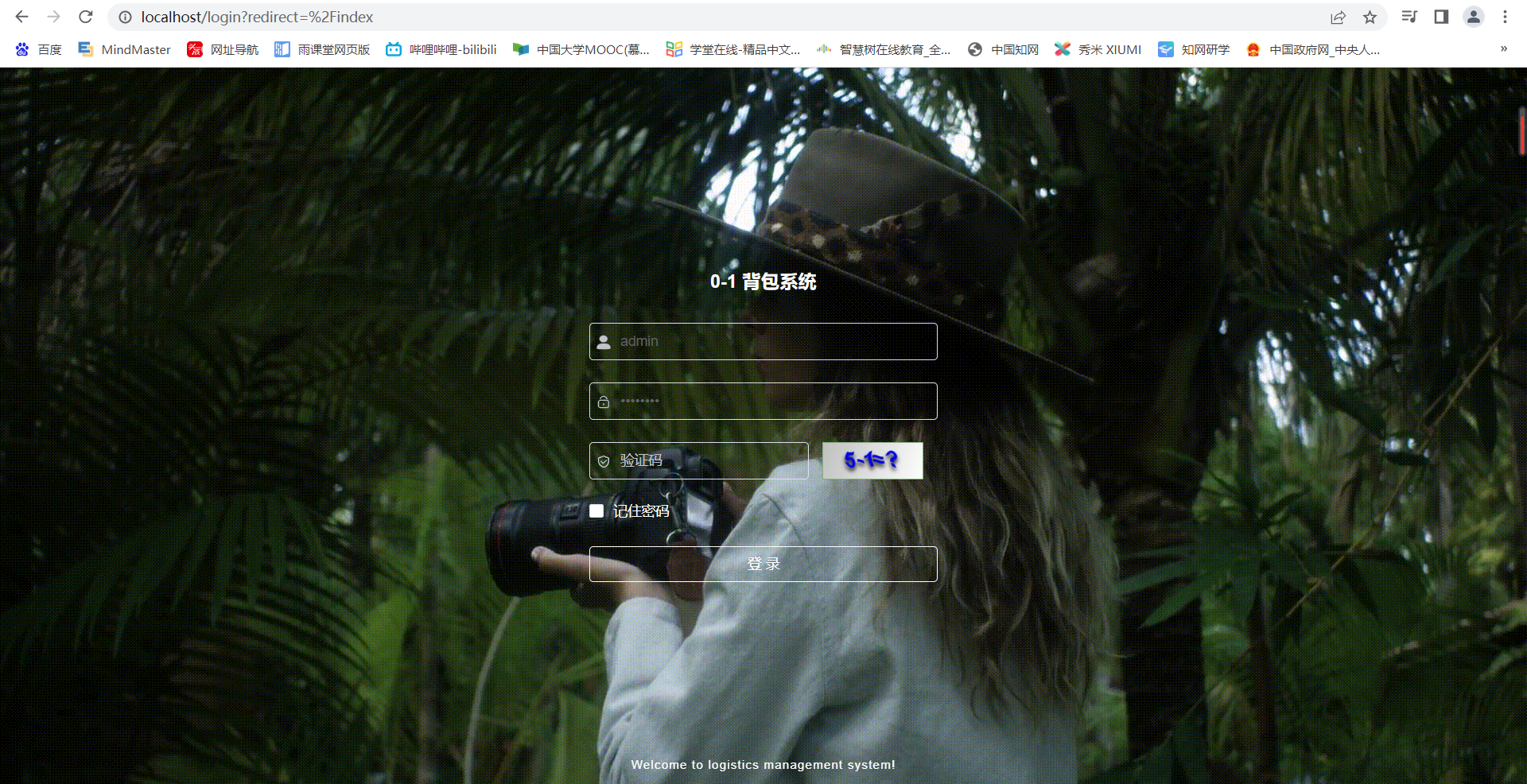
- (web主界面)
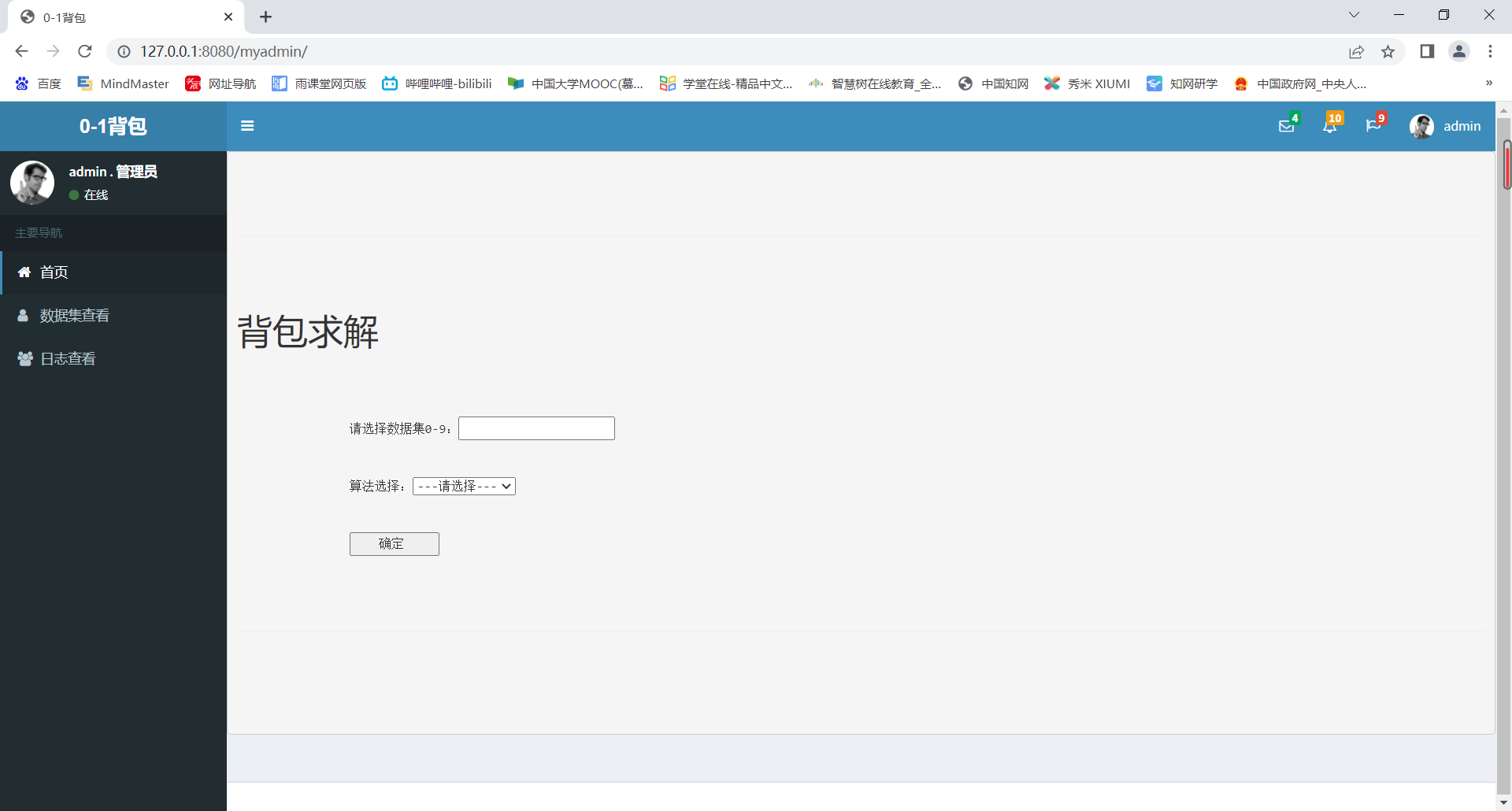
从数据库正确读取数据#
- (主界面选择数据)
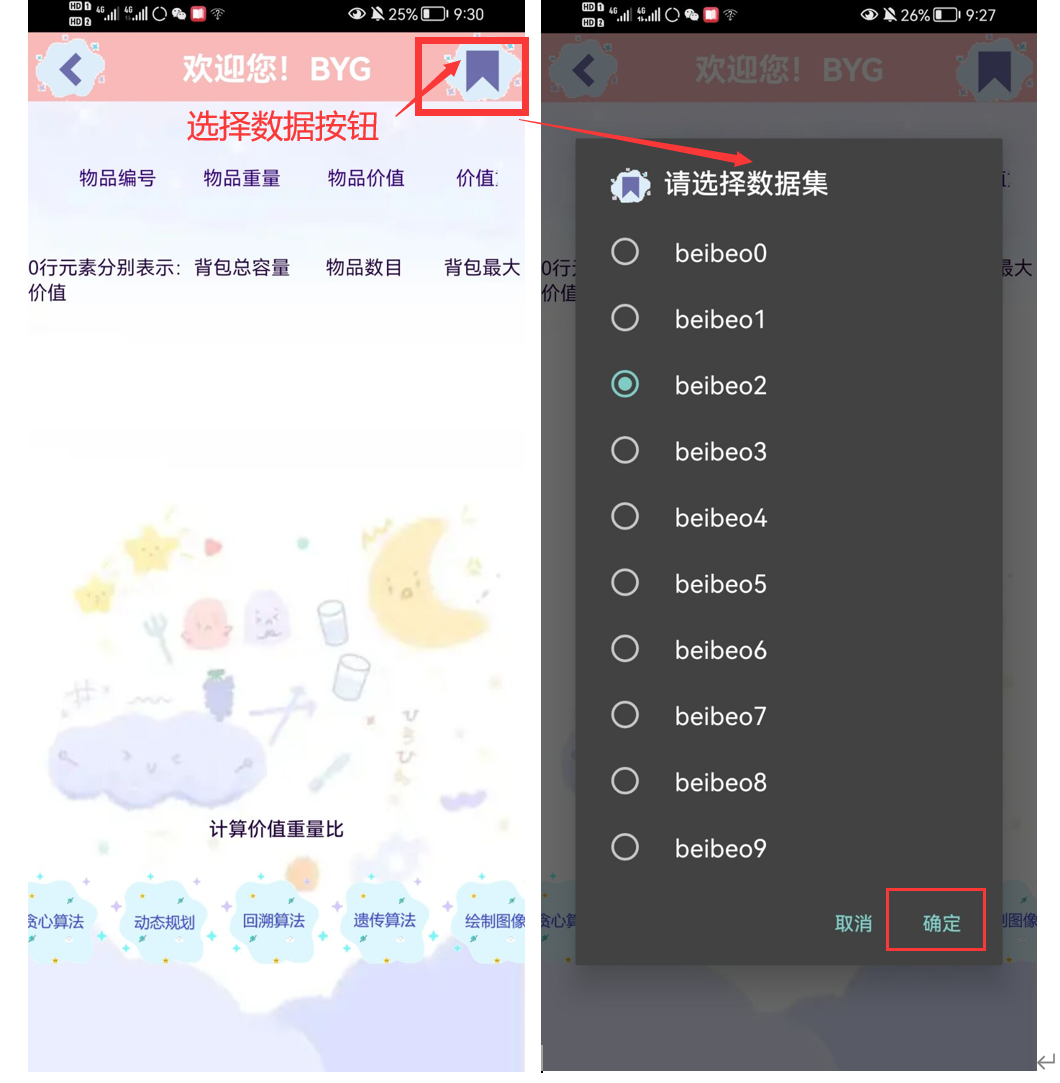
- (APP界面数据库信息读入,数据文件为beibao2)
- (web界面数据库信息)
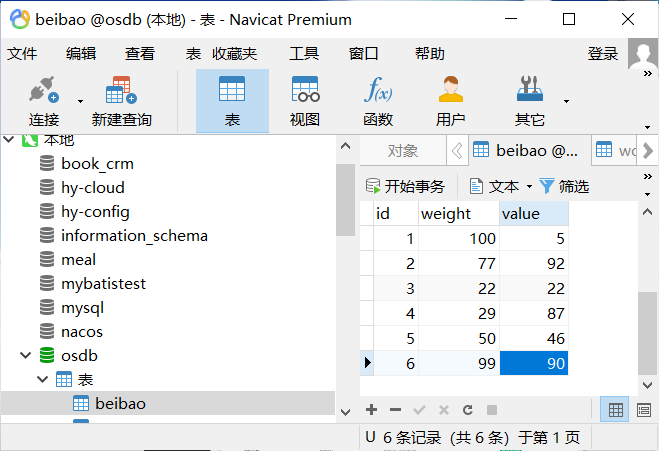
- (web界面显示从数据库所读取信息)
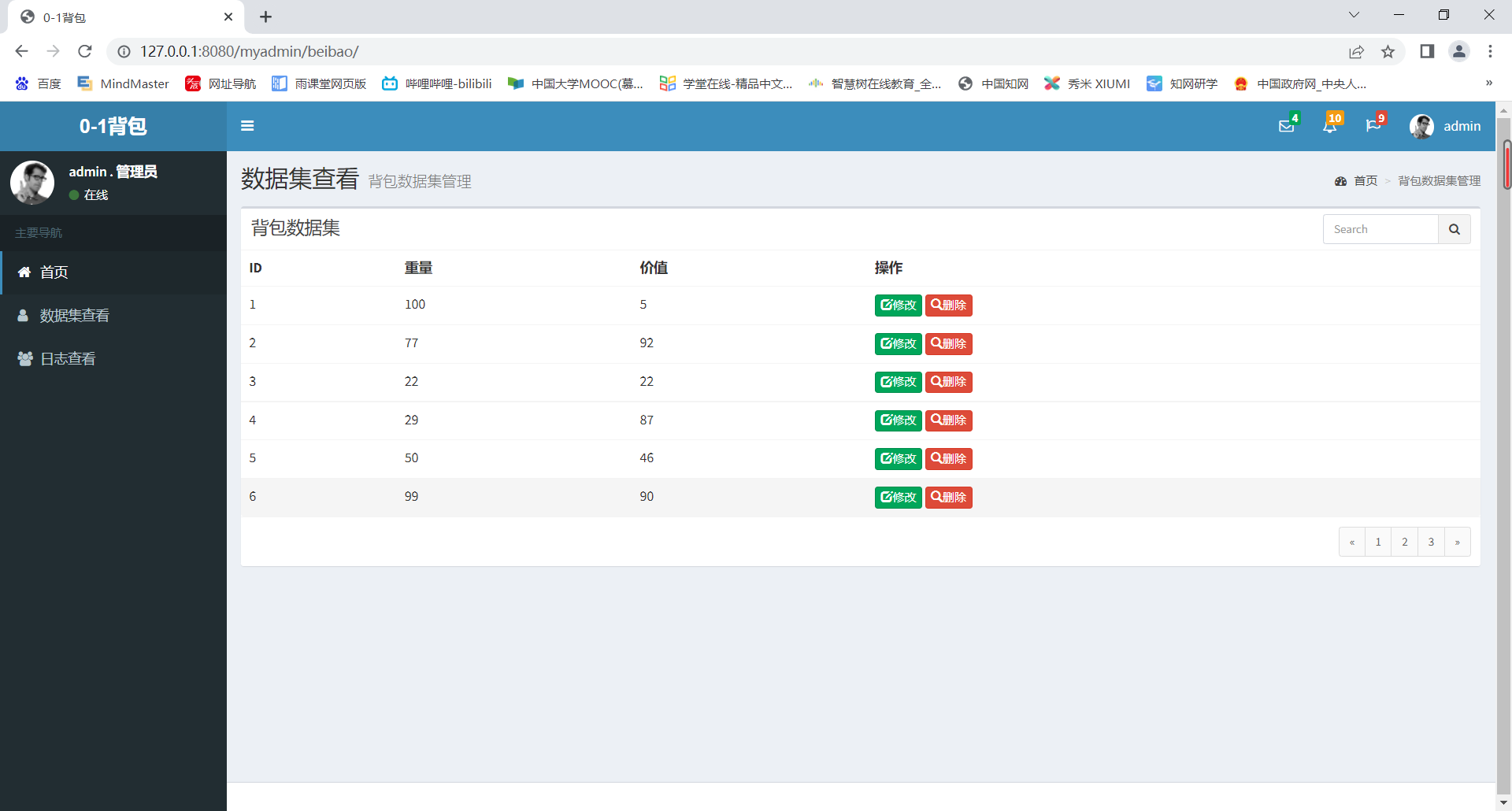
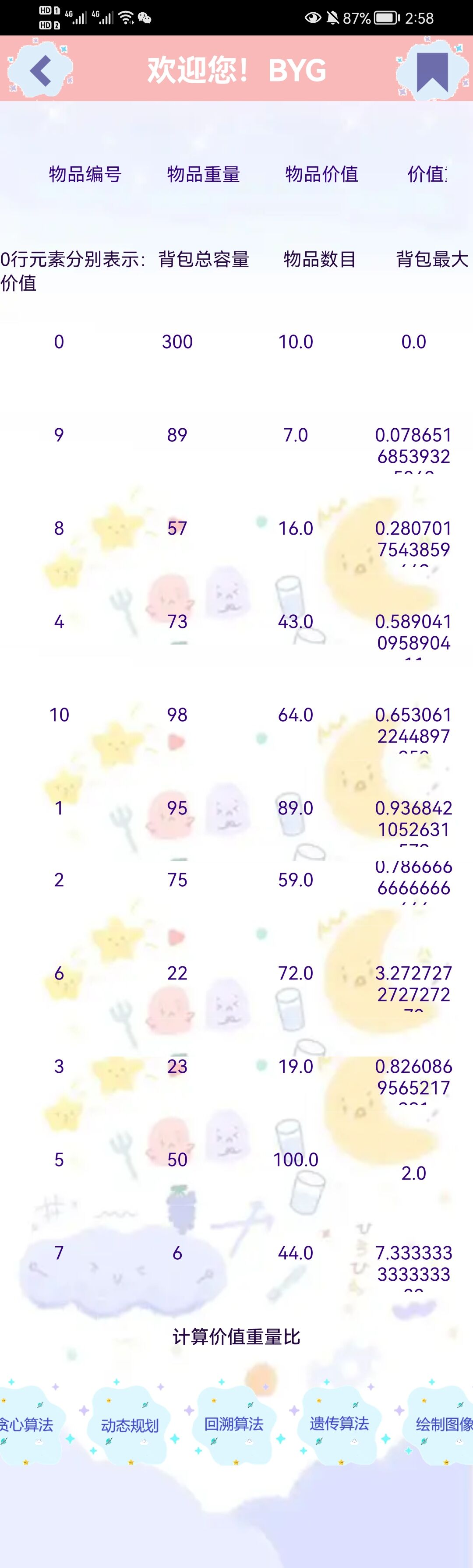
对物品按照价值重量比进行非降序排列#
- (数据文件为beibao2)
采用贪心算法求解#
- (数据文件为beibao2)

采用回溯算法求解#
- (数据文件为beibao6)

采用动态规划算法求解#
- (数据文件为beibao4)

采用遗传算法求解#
- (数据文件为beibao2)

绘制气泡图并保存#

绘制条形图并保存#
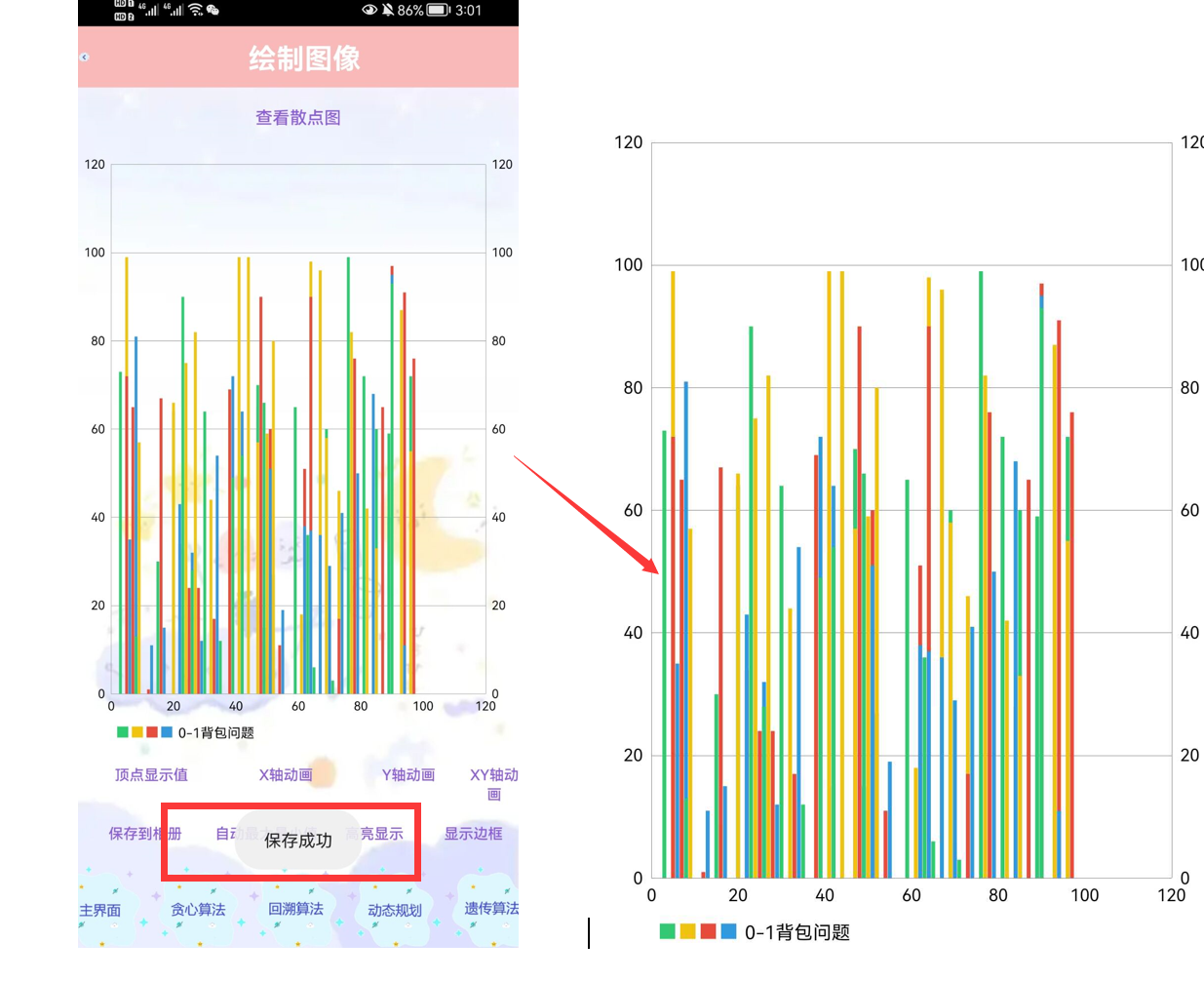
保存求解结果#
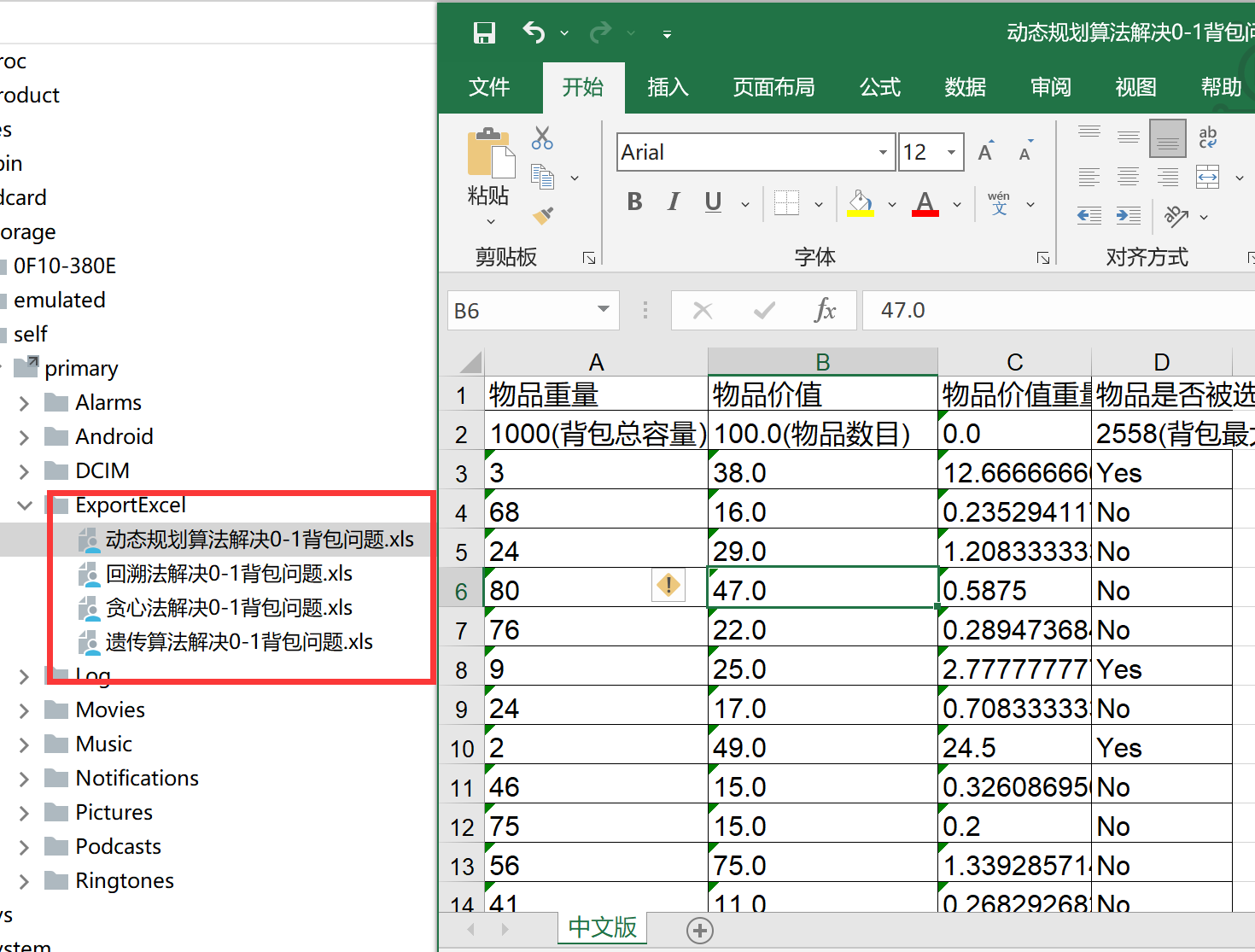
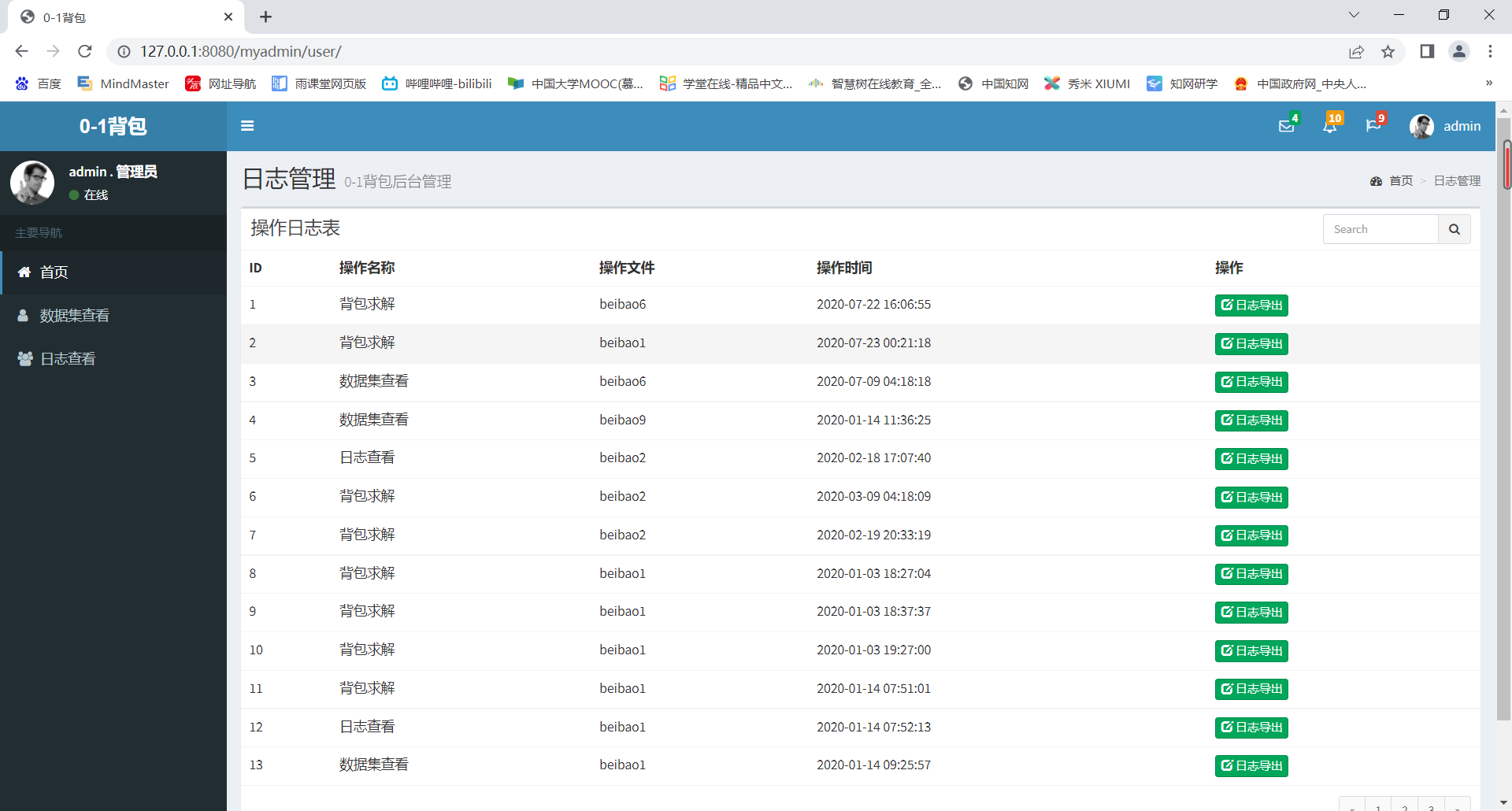
保存日志数据#
- (APP日志保存)

- (web界面日志保存)
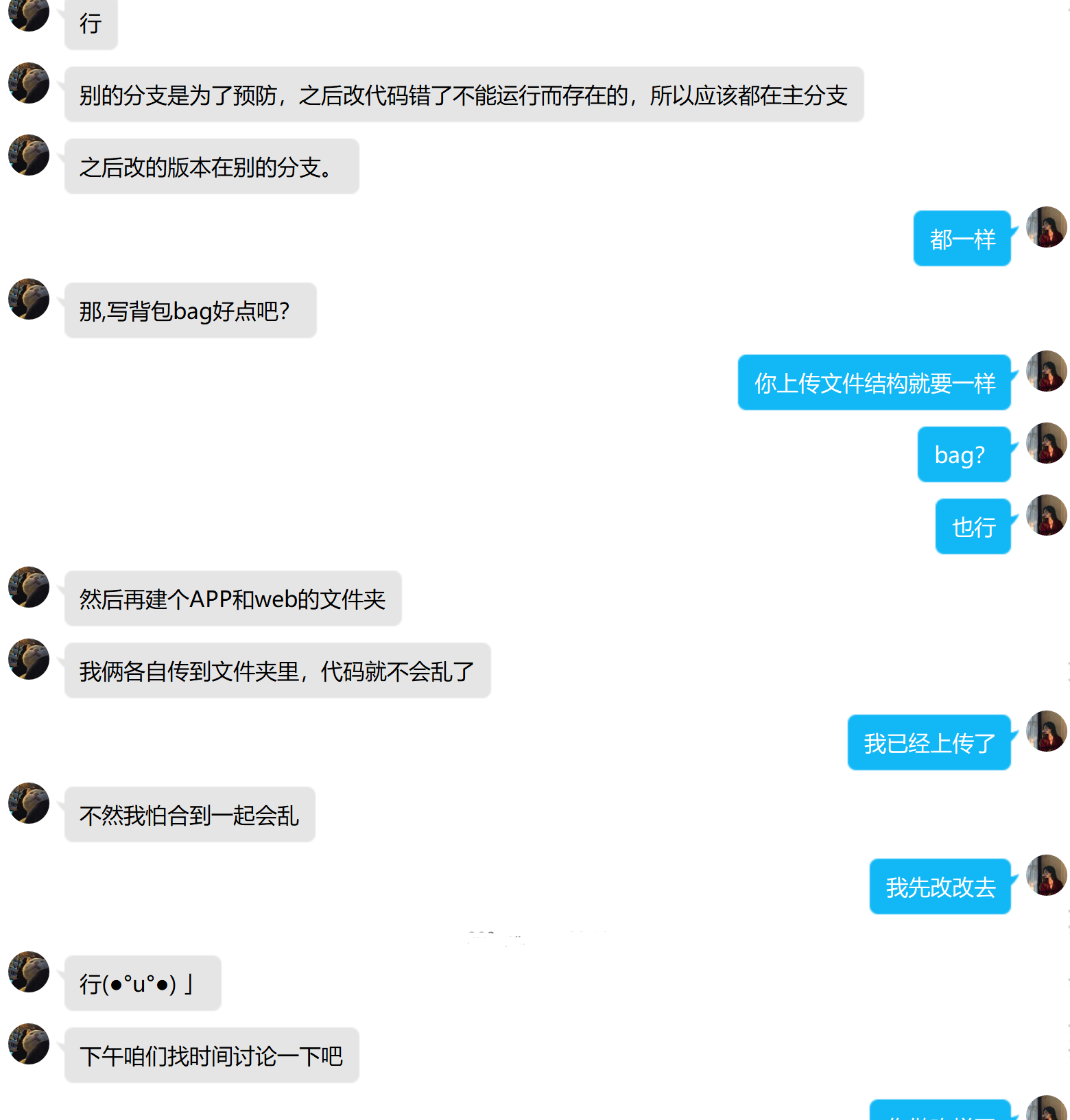
7.描述结对的过程,提供两人在讨论、细化和编程时的结对照片(非摆拍)#
- 两人在讨论、细化和编程时的结对照片
采用汉堡包法实施项目结对中两个人的沟通,部分截图如下所示:
- 项目仓库
-
共同commit操作
-
具体commit操作(部分截图)
-
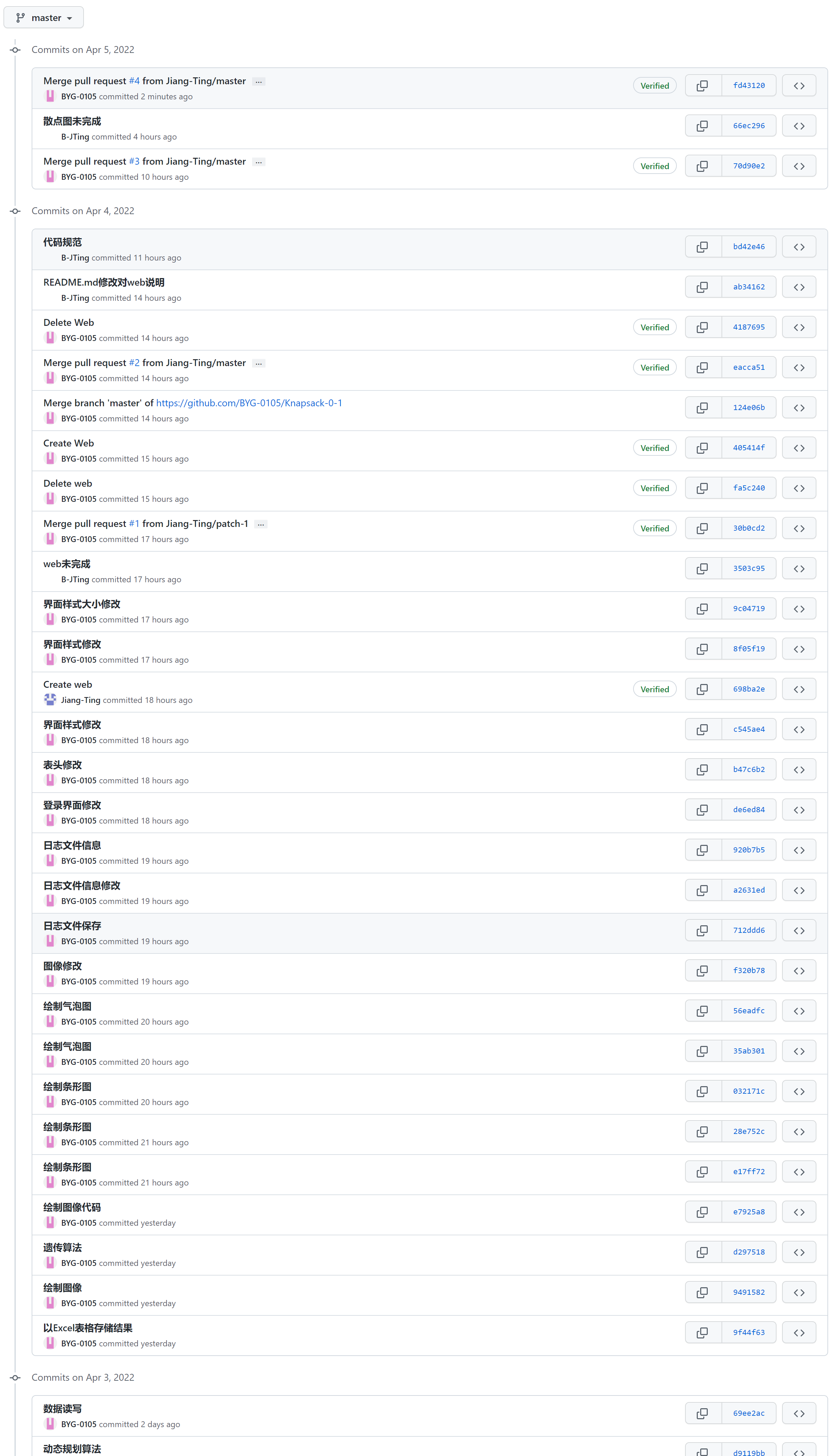
-
项目src文件夹

-
代码规范文件
8.此次结对作业的PSP#
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 20 | 40 |
| - Estimate | - 估计这个任务需要多少时间,并规划大致工作步骤 | 15 | 20 |
| Development | 开发 | 750 | 850 |
| - Analysis | - 需求分析(包括学习新技术) | 35 | 45 |
| - Design Spec | - 生产设计文档 | 30 | 35 |
| - Design Review | - 设计复审(和同事审核设计文档) | 30 | 25 |
| - Coding Standard | - 代码规范(为目前的开发指定合适的规范) | 20 | 30 |
| - Design | - 具体设计 | 50 | 45 |
| - Coding | - 具体编码 | 450 | 600 |
| - Code Review | - 代码复审 | 40 | 50 |
| - Test | - 测试(自我测试,修改代码,提交修改) | 130 | 120 |
| Reporting | 报告 | 110 | 145 |
| - Test Report | - 测试报告 | 60 | 70 |
| - Size Measurement | - 计算工作量 | 20 | 30 |
| - Postmortem & Process Improvement Plan | - 事后总结,并提出过程改进计划 | 30 | 45 |
9.小结感受:两人合作真的能够带来1+1>2的效果吗?通过这次结对合作,请谈谈感受和体会。#
通过此次两人结对合作,在两人的共同努力和探讨下,一起完成了此次项目,两人合作能够带来1+1>2的效果,在原先的学习生活中,对于一些项目的开发设计,通常都是一个人独自负责软件的开发编程,在开发过程中,总会遇到一些问题,但由于独立开发,没有同伴可以一起商量探讨,共同解决问题,使得开发效率大大降低,在此次项目中,采用结对编程的方式,两人共同开发一个项目,遇到问题可一起探讨,对于整体项目可分为不同的模块共同开发,这大大提高了软件项目开发效率,对我们来说是一次很好的学习机会。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 25岁的心里话
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 闲置电脑爆改个人服务器(超详细) #公网映射 #Vmware虚拟网络编辑器
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用