首先膜拜下wikipedia:
http://en.wikipedia.org/wiki/Discrete_cosine_transform
我们已经知道DFT将信号变换为复指数信号的线性组合,并且如果时域信号是偶对称的,那么频域将只有实部(复指数的余弦部分)。所以,如果将有限长信号延拓为偶对称的,就可以将其变换为余弦信号的线性组合。
以下面的原始信号作为例子
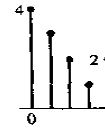
这个信号的长度为4。
DCT-1
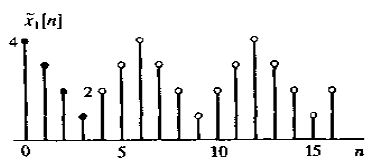
若原始信号长度为N,那么延拓后的时域周期为2N-2。
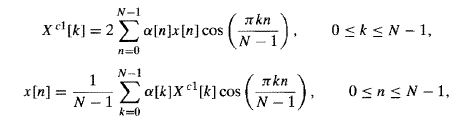
由于时域周期为2N-2,所以基频为cos(2PI/(2N-2))。求和区间本应为[0, 2N-2-1],考虑到余弦函数是偶函数,求和区间可以限定为[0, N-1],同时对x[n]加权,并将求和结果乘以2。
一倍频处,k=1,基函数为cos(πn/(N-1));
2N-3倍频处,k=2N-3,基函数为cos(π(2N-3)n/(N-1))=cos(π(2N-2-1)n/(N-1))=cos(π(2N-2)n/(N-1) - πn/(N-1))=cos(πn/(N-1))。
即1倍频和2N-3倍频有相同的基函数。
因此,DCT-1的结果X[k]与经过延拓后的时域信号具有相同的对称形式:
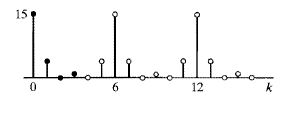
DCT-2

延拓后的时域周期为2N。
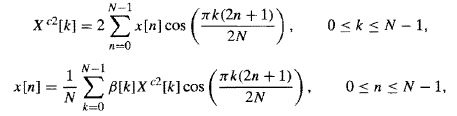
类似DCT-1,可以分别计算出1倍频和2N-1倍频处的基函数,它们相差一个负号。所以DCT-II的频域和时域图形*不*具备相同的对称形式:
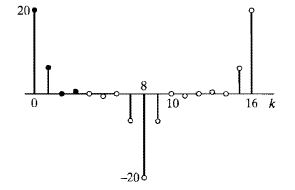
DCT-II变换式中的cos因子会出现非0相位,是因为拓展后的时域信号是关于半信号点对称的,而cos的零相位点对着这个对称点。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号