随机变量函数的分布与联合分布

以下文字均假设所求分布存在。

 

设函数y=f(x)单调递增，若随机变量X变化范围是[x, x+dx]，且由此引起的Y变化范围是[y, y+dy]，那么

P(x < X < x+dx)=P(y < Y < y+dy)

若单调递减，dy<0，上式就成为

P(x < X < x+dx)=P(y+dy < Y <y)

也就是：∫_x,x+dxf(x)dx=±∫_y,y+dyf(y)dy

上面两边分别微分，就有：

f_X(x)dx=f_Y(y)|dy|

若y=f(x)的反函数是x=h(y)，那么：

f_Y(y)=f_X(h(y))|dx/dy|

于是就得到随机变量函数的分布：

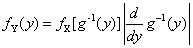
[式1]

直观上可以用最简单的例子y=kx和[0,1]上的均匀分布来理解(k>1)。 

y是[0,k]上的均匀分布。要保持密度函数积分为1，Y在单位长度上取值的概率将下降到原来的1/K，或者说按照dx/dy（斜率的倒数）下降。

 

随机变量函数的联合分布：

令

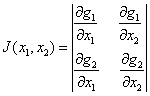
那么

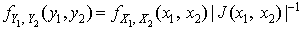
[式2]

 

以上两个求随机变量函数（联合）分布的式子实际上有共同的形式；

你只要用反函数求导公式将[式1]中的导数式子改写，就可以得到和[式2]类似的形态：

随机变量函数的（联合）分布等于：

用随机变量函数的反函数替换分布函数中的变量得到的式子-乘以-随机变量函数的反函数的导数。

-或-

用随机变量函数的反函数替换分布函数中的变量得到的式子-乘以-随机变量函数的雅可比行列式的倒数。