数据结构和算法(面试)

排序算法

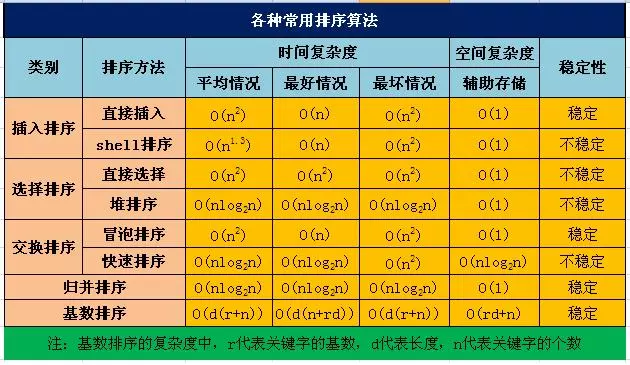
直接插入排序：将数组中的所有元素依次跟前面已经排好的元素相比较，如果选择的元素比已排序的元素小，则交换，直到全部元素都比较过

希尔排序：将待排序数组按照步长gap进行分组，然后将每组的元素利用直接插入排序的方法进行排序；每次将gap折半减小，循环上述操作；当gap=1时，利用直接插入，完成排序

简单选择排序：比较+交换

堆排序：构建大顶堆进行排序

如何手写一个堆
1. 插入一个数           heap[ ++ size ] = x; up(size);
2. 邱集合当中的最小值   heap[1]
3. 删除最小值           heap[1] = heap[size]; size --; down(1);
4. 删除任意一个元素     heap[k] = heap[size]; size --; down(k); up(k); 
5. 修改任意一个元素     heap[k] = x; down(k); up(k); 

堆排序

int n, m;
int h[ 1000 ], cnt;

void down( int u )
{
    int t = u;
    if( u * 2 <= cnt && h[ u * 2 ] < h[ t ] ) t = u * 2;
    if( u * 2 + 1 <= cnt && h[ u * 2 + 1 ] < h[ t ] ) t = u * 2 + 1;
    if( u != t )
    {
        swap( h[ u ], h[ t ] );
        down( t );
    }
}

void up( int u )
{
    while( u / 2 && h[ u ] < h[ u / 2 ] )
    {
        swap( h[ u ], h[ u / 2 ] );
        u >> = 1;
    }
}
 
int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ ) cin >> h[ i ];
    cnt = n;
    
    for( int i = n / 2; i; i -- ) down( i );

    while( m -- )
    {
        cin >> h[ 1 ] << " ";
        h[ 1 ] = h[ cnt -- ];
        down( 1 );
    }    
    return 0;
}

冒泡排序：

1. 将序列当中的左右元素，依次比较，保证右边的元素始终大于左边的元素

2. 对序列当中剩下的n-1个元素再次执行步骤1

3. 对于长度为n的序列，一共需要执行n-1轮比较

快速排序：挖坑填数+分治法

vector< int > quick_sort( vector<int> q, int l, int r )
{
    if( l >= r ) return;
    int i = l - 1;
    int j = r + 1;
    int x = q[l + r >> 1];
    while( i < j )
    {
          do i ++; while( q[ i ] < x );
          do j --; while( q[ j ] > x );
          if( i < j ) swap( q[ i ], q[ j ] );
    }
    quick_sort( q, l, j );
    quick_sort( q, j + 1, r );
}

归并排序：

1. 分解----将序列每次折半拆分

2. 合并----将划分后的序列段两两排序合并

vector< int > tmp;
void merge_sort( vector< int > q, int l, int r )
{
    if( l >= r ) return;
    auto mid = l + r >> 1;
    merge_sort( q, l, mid );
    merge_sort( q, mid + 1, r );
    int i = l;
    int j = mid + 1;
    int k = 0;
    while( i <= j )
    {
          if( q[i] <= q[j] ) tmp[ k ++ ] = q[ i ++ ];
          else                   tmp[ k ++ ] = q[ j ++ ];
    }
    while( i <= mid ) tmp[ k ++ ] = q[ i ++ ];
    while( j <= r )  tmp[ k ++ ] = q[ j ++ ];
    for( int i = l, j = 0; i <= r; i ++, j ++ ) q[ i ]  = tmp[ j ];
}

kmp算法

KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)

在朴素算法中，我们每次匹配失败都不得不放弃之前所有的匹配进度，因此时间复杂度很高，而

失配指针：位置

// 求失配数组
//即为一个模式串自身匹配自身的过程，刚刚说过失配数组是建立在模式串的意义下的，跟与文本串匹配思路一样
int n = s1.length();
int m = s2.legnth();
for( int i = 1; i < m; i ++ )
{
    while( k && s2[ i ] != s2[ k ] ) k = kmp[ k ];
    if( s2[ i ] = s2[ k ] ) kmp[ i + 1 ] = ++ k;
}

// 在文本串中找模式串
// 其中k可以看做表示当前已经匹配完的模式串的最后一位的位置，你也可以理解为表示模式串匹配到第几位了 

k = 0;
for( int i = 0; i < n; ++ i )
{
    while( k && s1[ i ] != s2[ k ] ) k = kmp[ k ];
    //匹配失败就沿着失配指针往回调，跳到模式串的第一位就不用再跳了。
    if( s1[ i ] == s2[ k ] ) ++ k;    //匹配成功那么匹配到的模式串位置+1
    if( k == m ) cout << i - m + 2 << endl;    //找到一个模式串，输出位置即可。
}

图的关键路径

无向图的一个更重要的用途是关键路径分析法。每个节点表示要给必须执行的动作以及完成动作所花费的时间。因此，该图为动作节点图

图中的边代表优先关系：一条边(v,w)意味着动作v必须在动作w开始前完成。

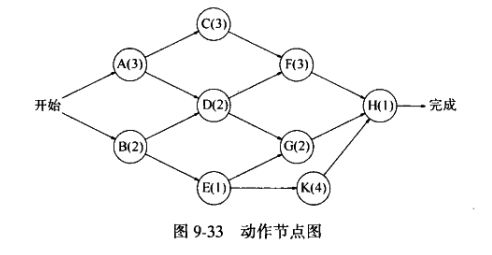
开始最后一件事情的条件是前置事件全部完成，前置事件互相之间可以并行指定，但最早完成时间就是最长路径

posted @ 2020-04-06 03:42 byene 阅读(560) 评论(0) 编辑收藏举报

刷新页面返回顶部