深入学习二叉树(04)平衡二叉树
一、AVL 树简介
AVL树的名字来源于它的发明作者G.M. Adelson-Velsky 和 E.M. Landis。AVL树是最先发明的自平衡二叉查找树(Self-Balancing Binary Search Tree,简称平衡二叉树)
使用对象: AVL 树适应于插入与删除次数比较少,但是查找多的情况,是严格的二叉平衡树,旋转是非常耗时的
平衡二叉树的定义(AVL)
它或者是一棵空树,或者具有以下性质的二叉树:它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一棵平衡二叉树
一棵AVL 树有如下必要条件:
1. 它必须是二叉查找树 2. 每个节点的左子树和右子树的高度差不超过 1
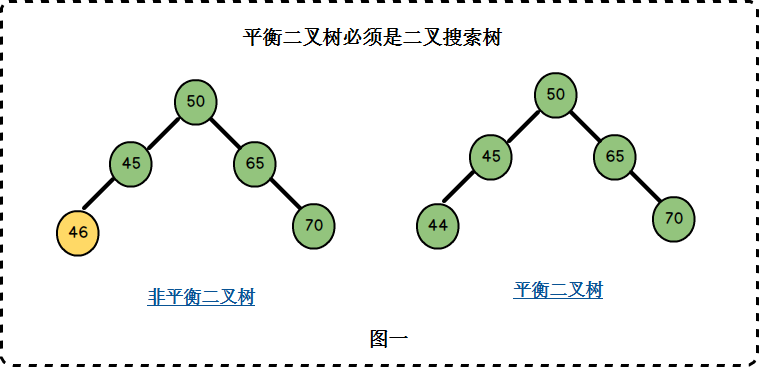
图一中左边二叉树的节点45的左孩子46比45大,不满足二叉搜索树的条件,因此它也不是一棵平衡二叉树。
右边二叉树满足二叉搜索树的条件,同时它满足条件二,因此它是一棵平衡二叉树

左边二叉树的节点45左子树高度2,右子树高度0,左右子树高度差为2-0=2,不满足条件二;
右边二叉树的节点均满足左右子树高度差至多为1,同时它满足二叉搜索树的要求,因此它是一棵平衡二叉树。
AVL树的查找、插入、删除操作在平均和最坏的情况下都是O(logn),这得益于它时刻维护着二叉树的平衡。如果我们需要查找的集合本身没有顺序,在频繁查找的同时也经常的插入和删除,AVL树是不错的选择。不平衡的二叉查找树在查找时的效率是很低的,因此,AVL如何维护二叉树的平衡是我们的学习重点
二、AVL 树相关的概念
2.1 平衡因子:将二叉树上节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)
节点50的左子树高度为3,右子树高度为2,BF= 3-2 = 1;
节点45的左子树高度为2,右子树高度为1,BF= 2-1 = 1;
节点46的左子树高度为0,右子树高度为0,BF= 0-0 = 0;
节点65的左子树高度为0,右子树高度为1,BF= 0-1 = -1;
对于平衡二叉树,BF的取值范围为[-1,1]。如果发现某个节点的BF值不在此范围,则需要对树进行调整。
2.2 最小不平衡子树:距离插入节点最近的,且平衡因子的绝对值大于1的节点为根的子树
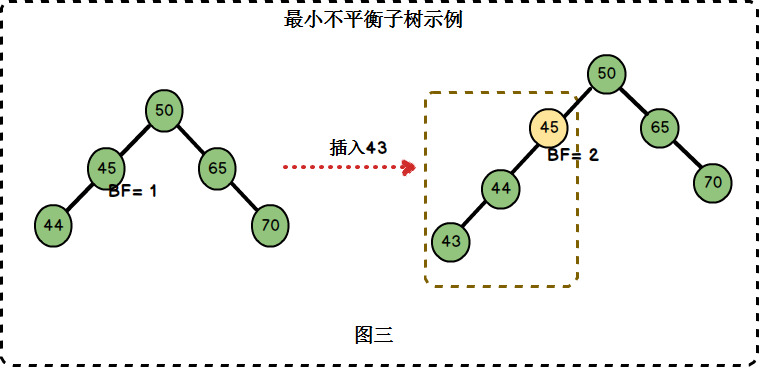
在图三中,左边二叉树的节点45的BF = 1,插入节点43后,节点45的BF = 2。节点45是距离插入点43最近的BF不在[-1,1]范围内的节点,因此以节点45为根的子树为最小不平衡子树。
三、AVL 树的平衡调整
定义平衡二叉树节点结构:
typedef struct Node { int key; struct Node *left; struct Node *right; int height; }BTNode;
整个实现过程是通过在一棵平衡二叉树中依次插入元素(按照二叉排序树的方式),若出现不平衡,则要根据新插入的结点与最低不平衡结点的位置关系进行相应的调整。
分为LL型、RR型、LR型和RL型4种类型,各调整方法如下(下面用A表示最低不平衡结点):
3.1LL 型调整
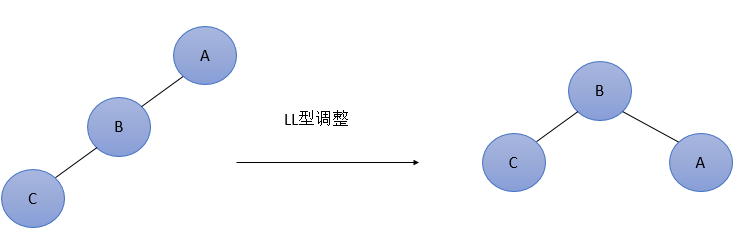
由于在A的左孩子(L)的左子树(L)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由1增至2。下面图1是LL型的最简单形式。显然,按照大小关系,结点B应作为新的根结点,
其余两个节点分别作为左右孩子节点才能平衡,A结点就好像是绕结点B顺时针旋转一样。
LL型调整的一般形式如下图2所示,表示在A的左孩子B的左子树BL(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下:
- ①将A的左孩子B提升为新的根结点;
- ②将原来的根结点A降为B的右孩子;
- ③各子树按大小关系连接(BL和AR不变,BR调整为A的左子树)。
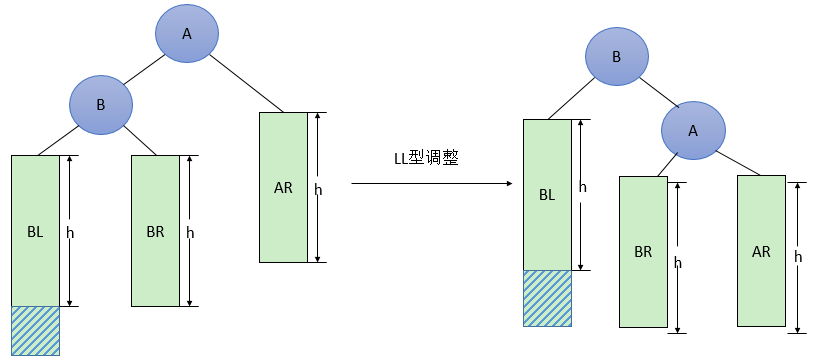
图2 一般形式的LL型调整
代码实现:
3.2 RR 型调整
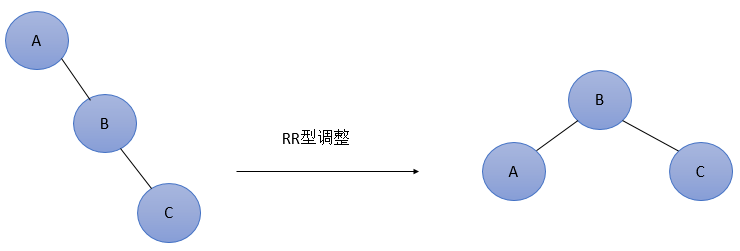
由于在A的右孩子(R)的右子树(R)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由-1变为-2。图3是RR型的最简单形式。显然,按照大小关系,
结点B应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡,A结点就好像是绕结点B逆时针旋转一样。
RR型调整的一般形式如下图4所示,表示在A的右孩子B的右子树BR(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下:
将A的右孩子B提升为新的根结点;
将原来的根结点A降为B的左孩子
各子树按大小关系连接(AL和BR不变,BL调整为A的右子树)。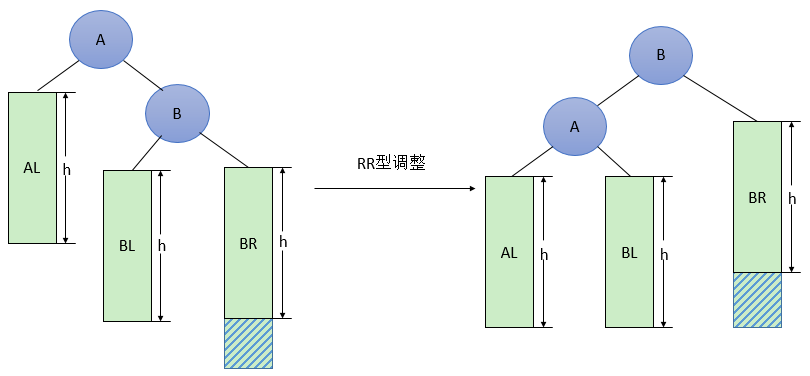
图4 一般形式的RR型调整
代码实现:
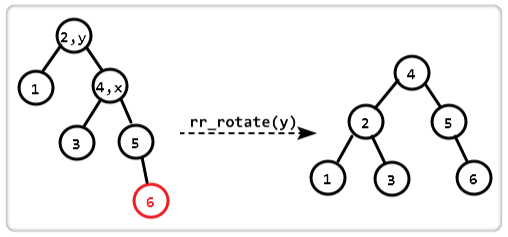
3.3 LR 型调整
由于在A的左孩子(L)的右子树(R)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由1变为2。图5是LR型的最简单形式。显然,按照大小关系,
结点C应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡。
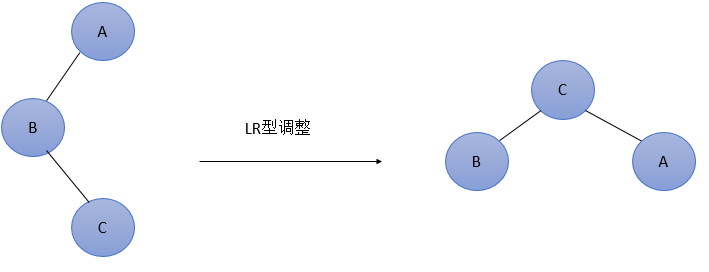
图5 最简单的LR型调整
LR型调整的一般形式如下图6所示,表示在A的左孩子B的右子树(根结点为C,不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。
这种情况调整如下:
- ①将B的左孩子C提升为新的根结点;
- ②将原来的根结点A降为C的右孩子;
- ③各子树按大小关系连接(BL和AR不变,CL和CR分别调整为B的右子树和A的左子树)。

图6 一般形式的LR型调整
代码实现
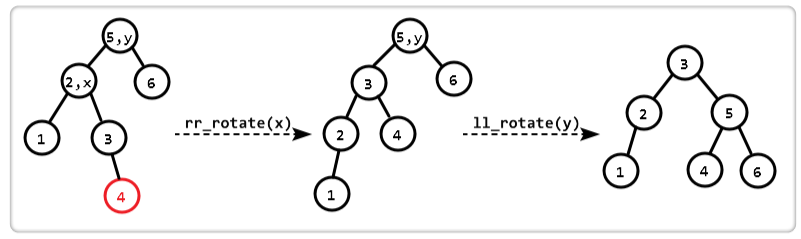
3.4 RL型调整
由于在A的右孩子(R)的左子树(L)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由-1变为-2。图7是RL型的最简单形式。显然,按照大小关系,
结点C应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡。
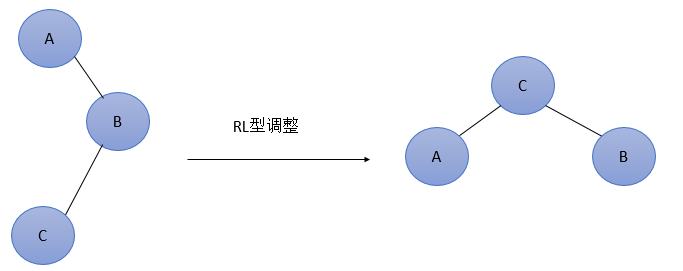
图7 最简单的RL型调整
RL型调整的一般形式如下图8所示,表示在A的右孩子B的左子树(根结点为C,不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)
这种情况调整如下:
- ①将B的左孩子C提升为新的根结点;
- ②将原来的根结点A降为C的左孩子;
- ③各子树按大小关系连接(AL和BR不变,CL和CR分别调整为A的右子树和B的左子树)。
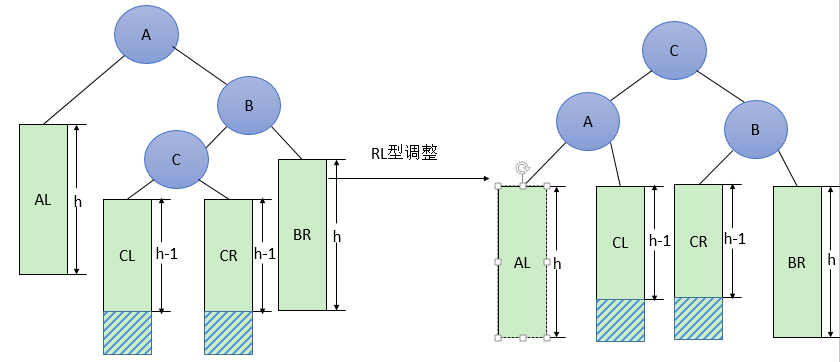
图8 一般形式的RL型调整
代码实现
平衡二叉树实现的实例
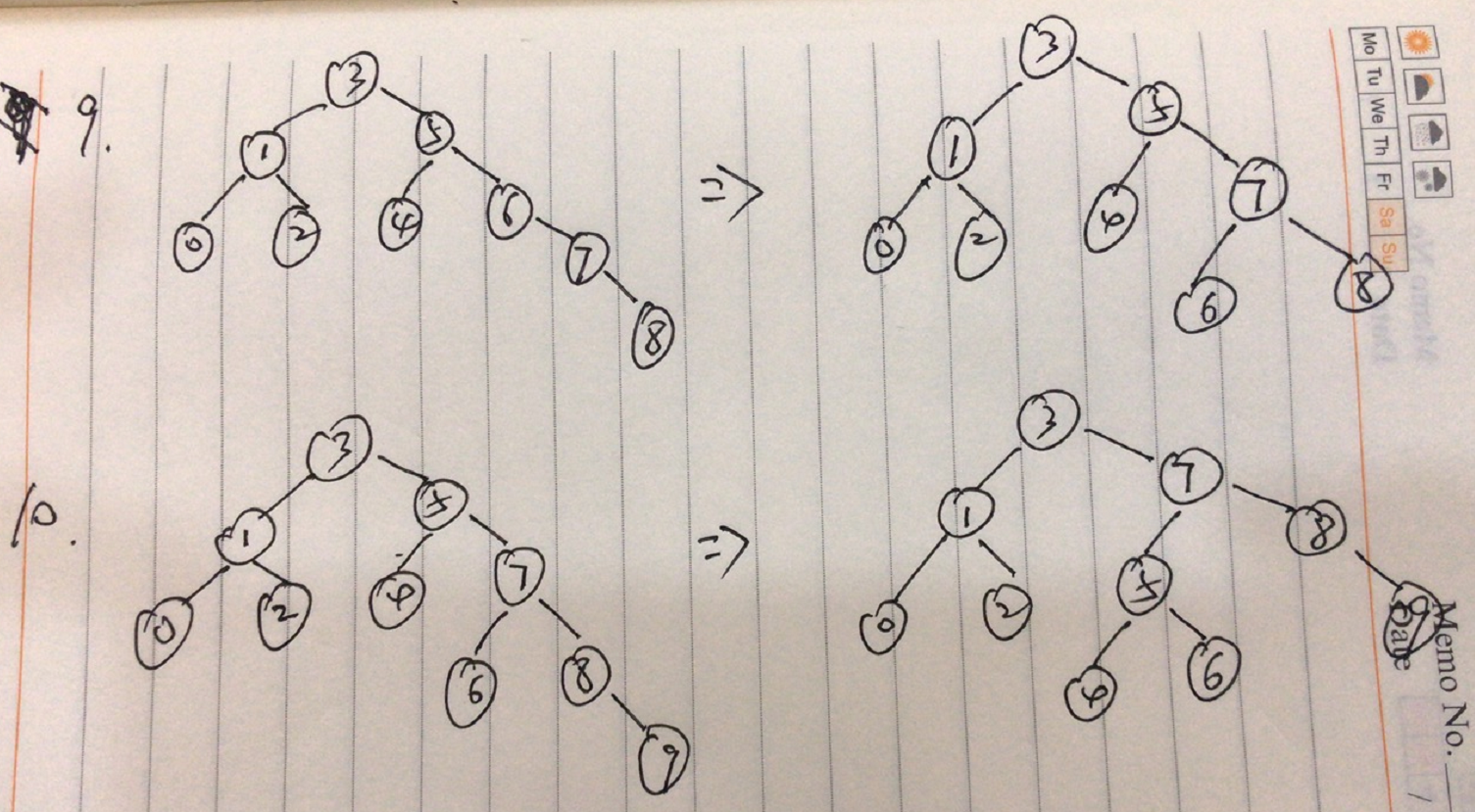
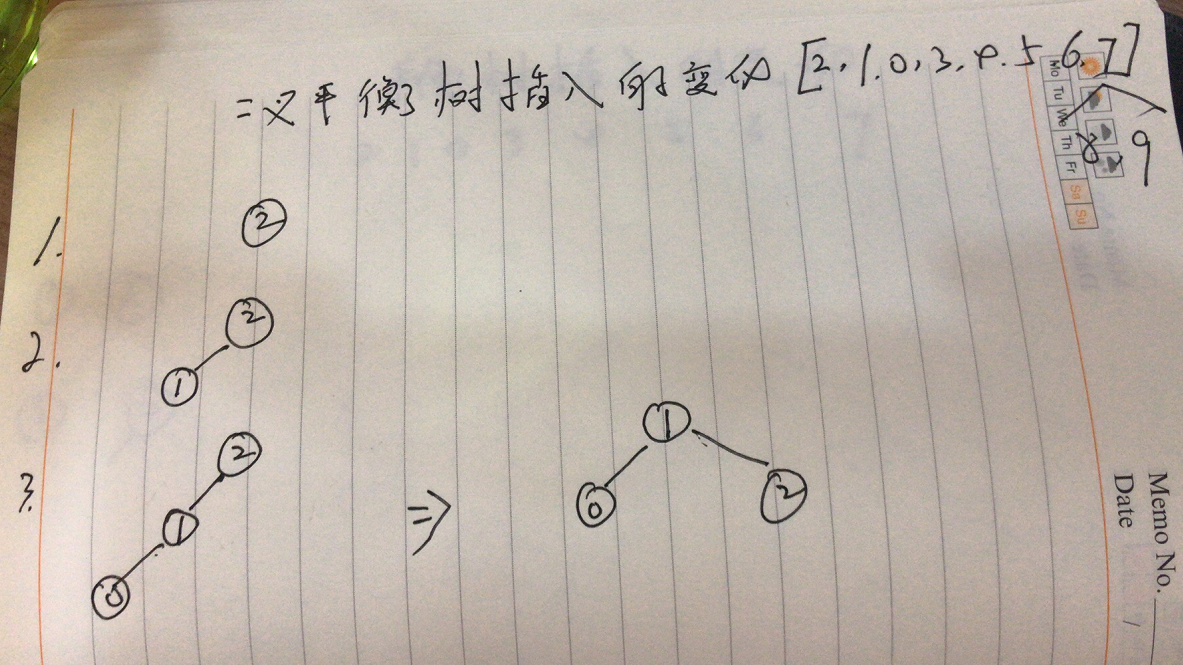
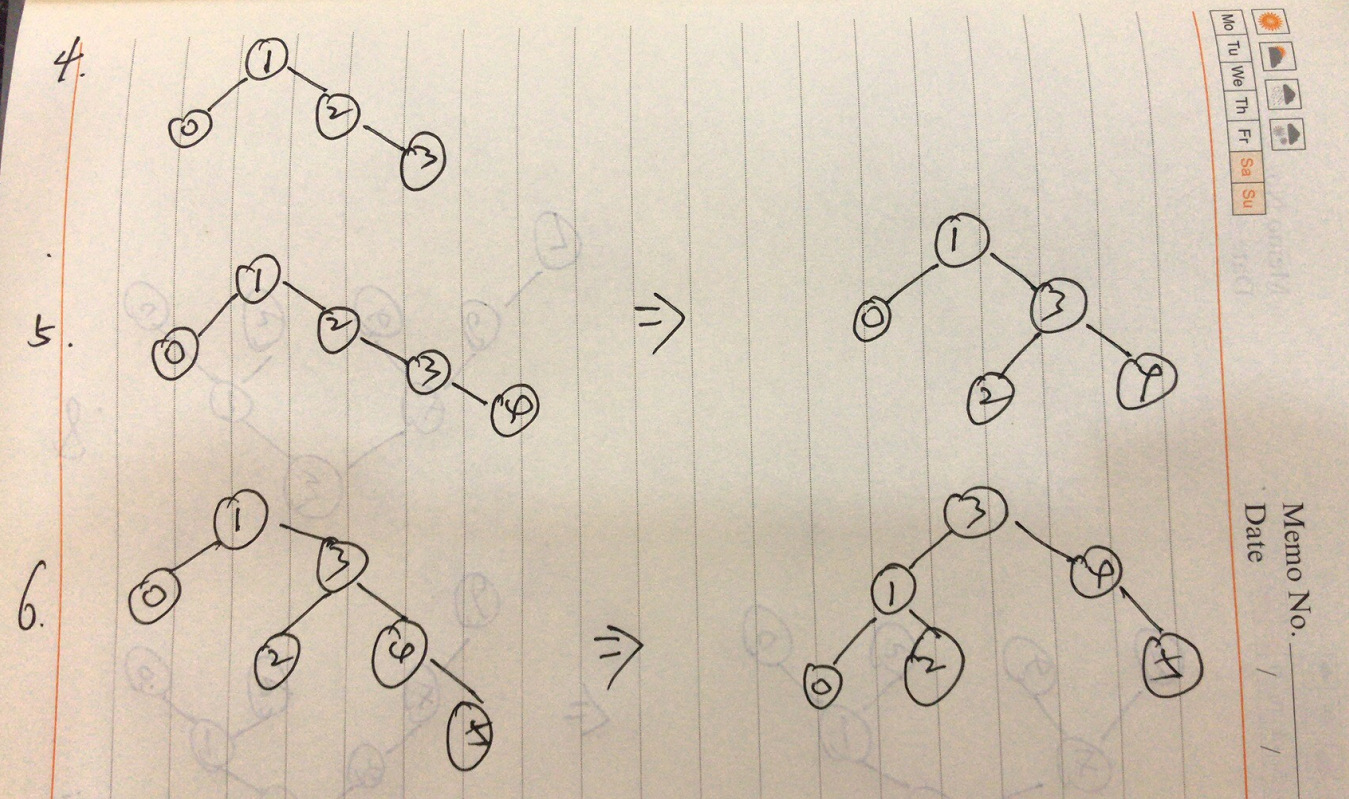
选取一组数据分别为2,1,0,3,4,5,6,9,8,7的10个结点来构造平衡二叉树。
- 首先数据为2的结点作为根结点插入,接着插入1,仍是平衡的,再插入0是,2的平衡因子变为2,此时出现了不平衡,因此需要进行调整,最低不平衡结点为2,属于LL型,调整过程如下图所示
- 接着插入3,是平衡的,再插入4,此时出现了不平衡,结点 1 和 2 的平衡因子都为 -2,结点2为最低不平衡结点,属于RR型,调整过程如下图所示
- 接着插入5,此时结点 1 的平衡因子为 -2,导致不平衡,结点1为最低不平衡结点,属于RR型,调整如下图所示。
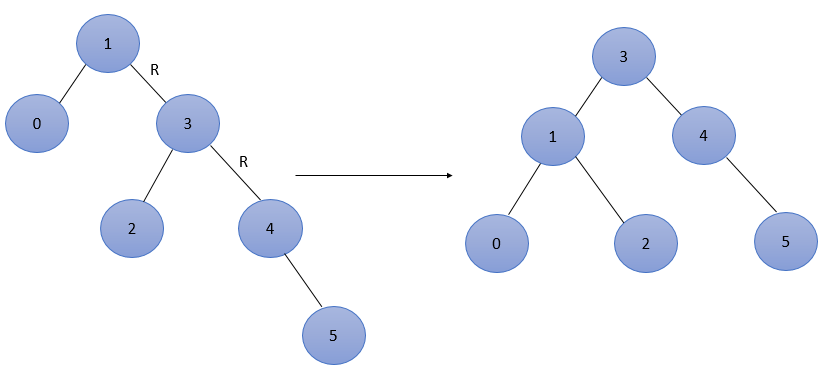
着插入6,此时结点4的平衡因子为 -2,导致不平衡,结点4为最低不平衡结点,属于RR型,调整如下图所示。

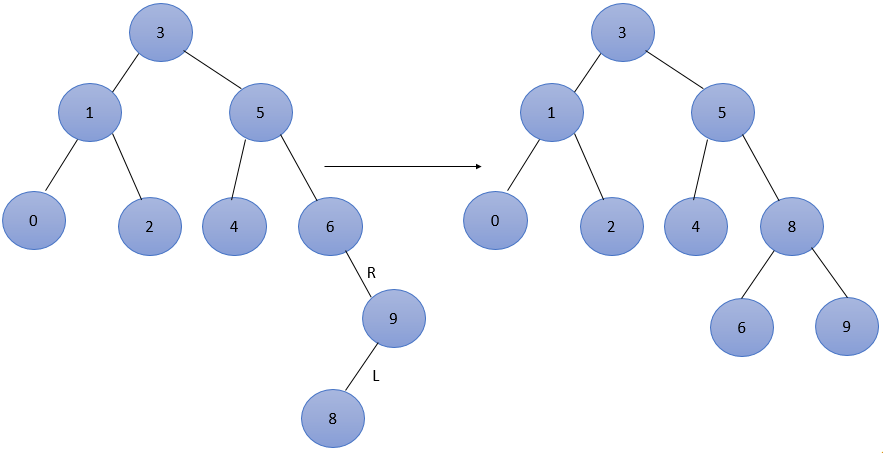
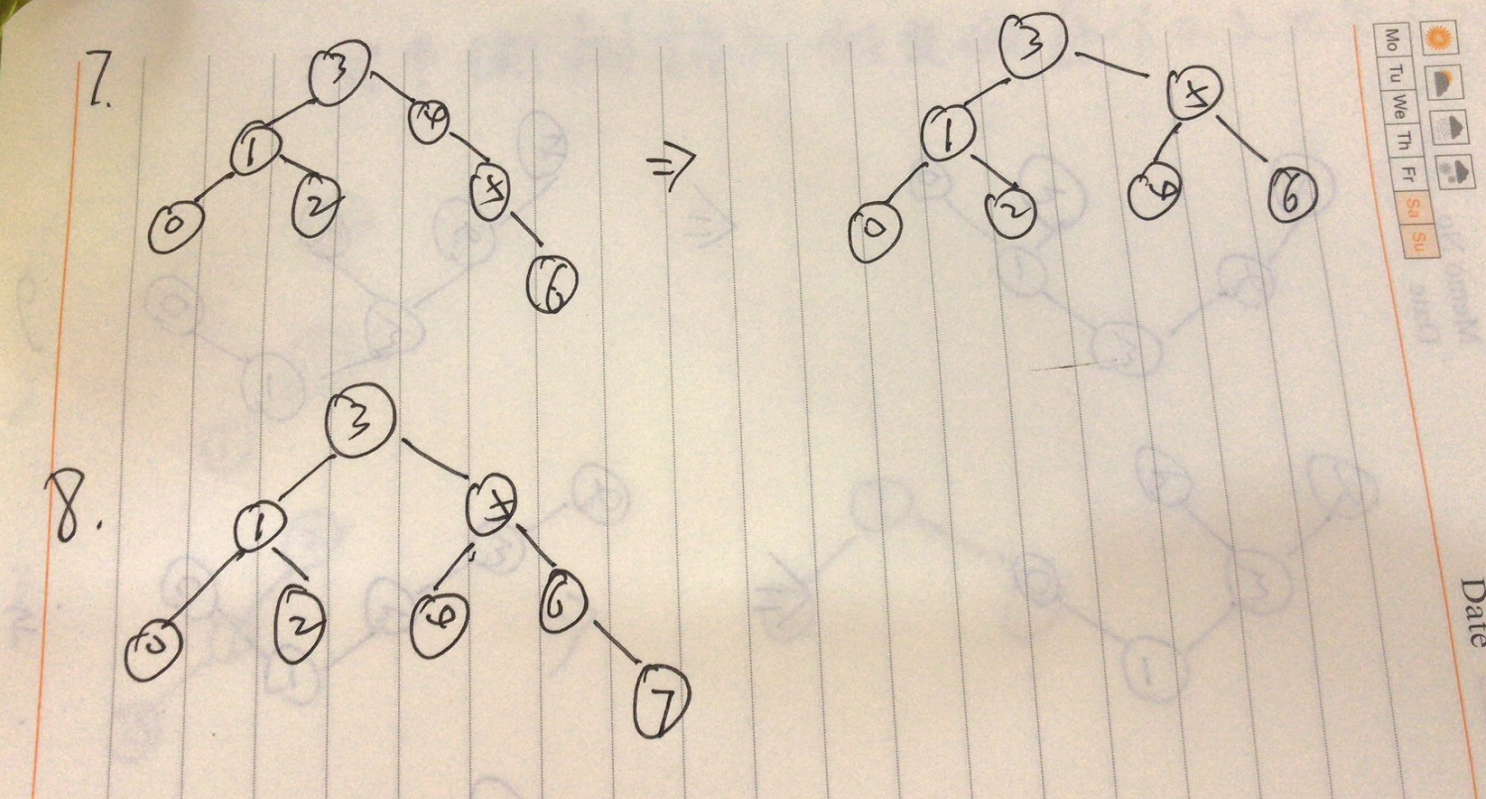
- 接着插入9,是平衡的,再插入8,此时结点 3、5、6 的平衡因子都为 -2,导致不平衡,结点6为最低不平衡结点,属于RL型,调整如下图所示
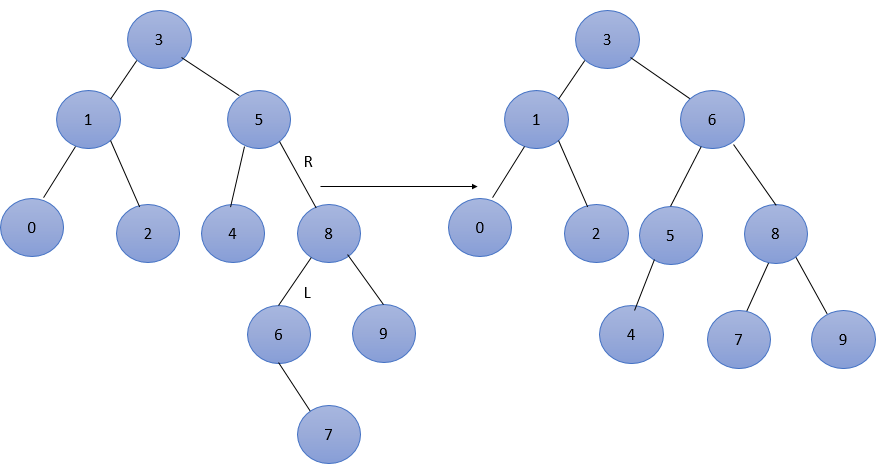
- 插入7,此时结点3、5的平衡因子为 -2,导致不平衡,最低不平衡结点为5,属于RL型,调整如下图所示。
完整代码:
#include<stdio.h>
#include<stdlib.h>
typedef struct root{
int key;
struct root *left,*right;
int height;
}Treeroot;
//声明函数
int max(int a,int b);
int height(Treeroot *root);
int getBalance(Treeroot *root);
Treeroot* ll_rotate(Treeroot* y);
Treeroot* rr_rotate(Treeroot *y);
Treeroot* newroot(int key);
Treeroot* insert(Treeroot *root,int key);
void print(Treeroot * root);
void preOrder(Treeroot *root,int tag);
Treeroot* minValueroot(Treeroot *root);
int max(int a,int b){
return (a>b)?a:b;
}
int height(Treeroot *root){
if(root == NULL)
return 0;
return root->height;
}
int getBalance(Treeroot *root){
if(root == NULL) return 0;
return height(root->left)-height(root->right);
}
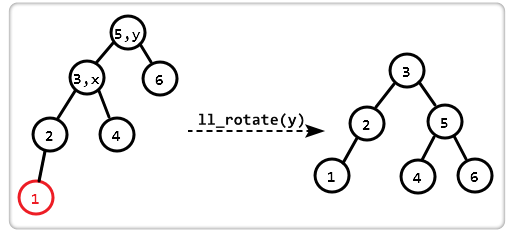
Treeroot* ll_rotate(Treeroot* root){
Treeroot *p = root->left;
root->left = p->right;
p->right = root;
root->height = max(height(root->left),height(root->right))+1;
p->height = max(height(p->left),height(p->right))+1;
return p;
}
Treeroot* rr_rotate(Treeroot *root){
Treeroot *p = root->right;
root->right = p->left;
p->left = root;
root->height = max(height(root->left),height(root->right))+1;
p->height = max(height(p->left),height(p->right))+1;
return p;
}
Treeroot* newroot(int key){
Treeroot *root = (Treeroot *)malloc(sizeof(Treeroot));
root->key = key;
root->left = NULL;
root->right = NULL;
root->height = 1;
return root;
}
Treeroot* insert(Treeroot *root,int key){
if(root==NULL)
return newroot(key);
if(key<root->key)
root->left = insert(root->left,key);
else if(key>root->key)
root->right = insert(root->right,key);
else
return root;
root->height = 1+max(height(root->left),height(root->right));
int balance = getBalance(root);
if(balance >1 && key < root->left->key)
return ll_rotate(root);
if(balance <-1 && key>root->right->key)
return rr_rotate(root);
if(balance >1 && key >root->left->key){
root->left = rr_rotate(root->left);
return ll_rotate(root);
}
if(balance <-1 && key<root->right->key){
root->right = ll_rotate(root->right);
return rr_rotate(root);
}
return root;
}
Treeroot* minValueroot(Treeroot *root){
Treeroot *current = root;
while(current->left!=NULL){
current=current->left;
}
return current;
}
void print(Treeroot *root){
if(root != NULL){
print(root->left);
printf("key:%3d,height:%3d\n",root->key,root->height);
print(root->right);
}
}
Treeroot* deleteroot(Treeroot *root,int key){
if(root == NULL)
return root;
if(key < root->key)
root->left = deleteroot(root->left,key);
else if(key > root->key)
root->right = deleteroot(root->right,key);
else{
if((root->left == NULL)||(root->right == NULL)){
Treeroot *temp = root->left?root->left : root->right;
if(temp == NULL){
temp = root;
root = NULL;
}else{
*root = * temp;
}
free(temp);
}else{
Treeroot *temp = minValueroot(root->right);
root->key = temp->key;
root->right = deleteroot(root->right,temp->key);
}
}
if(root ==NULL)
return root;
if (root == NULL)
return root;
root->height = 1 + max(height(root->left), height(root->right));
int balance = getBalance(root);
if (balance > 1 && getBalance(root->left) >= 0) //LL型
return ll_rotate(root);
if (balance > 1 && getBalance(root->left) < 0) //LR型
{
root->left = rr_rotate(root->left);
return ll_rotate(root);
}
if (balance < -1 && getBalance(root->right) <= 0) //RR型
return rr_rotate(root);
if (balance < -1 && getBalance(root->right) > 0) //Rl型
{
root->right = ll_rotate(root->right);
return rr_rotate(root);
}
return root;
}
int main(void){
Treeroot *root = NULL;
root = insert(root, 2);
root = insert(root, 1);
root = insert(root, 0);
root = insert(root, 3);
root = insert(root, 4);
root = insert(root, 5);
root = insert(root, 6);
root = insert(root, 9);
root = insert(root, 8);
root = insert(root, 7);
printf("\n中序遍历:\n");
//输出
print(root);
//删除某个节点
// printf("\n--------------------------\n");
// printf("删除节点 :7\n");
// root = deleteroot(root,7);
//
// //输出
// print(root);
return 0;
}

图一
图二
图三
图四