TensorFlow基础入门(三)

标签是我们要预测的真实事物:y线性回归中的y变量

特征是指用于描述数据的输入变量:xi线性回归中的[x1,x2,.....xn]

样本是指数据的特定实例:x

有标签样本具有｛特征，标签｝：｛x，y｝用于训练模型

无标签样本具有{特征，？}：｛x，?｝用于对新数据做出预测

模型可将样本映射到预测标签:y'　　由模型的内部参数定义，这些内部参数值是通过学习得到的

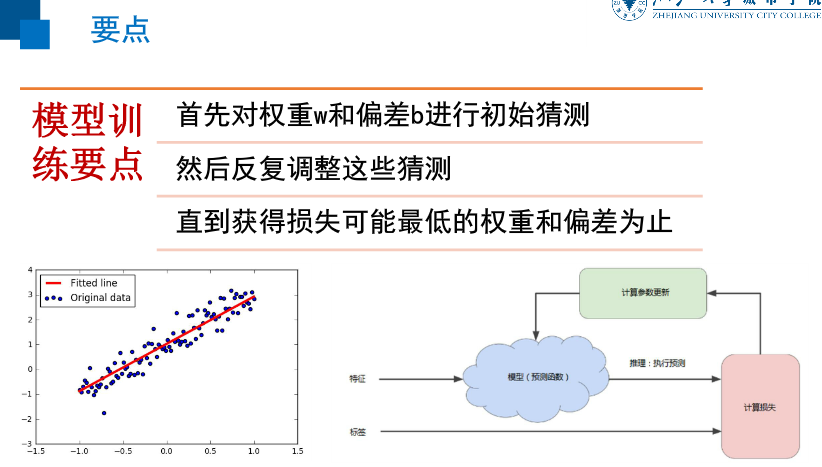
训练模型表示通过有标签样本来学习（确定）所有权重和偏差的理想值

在监督式学习中，机器学习算法通过以下方式构建模型:

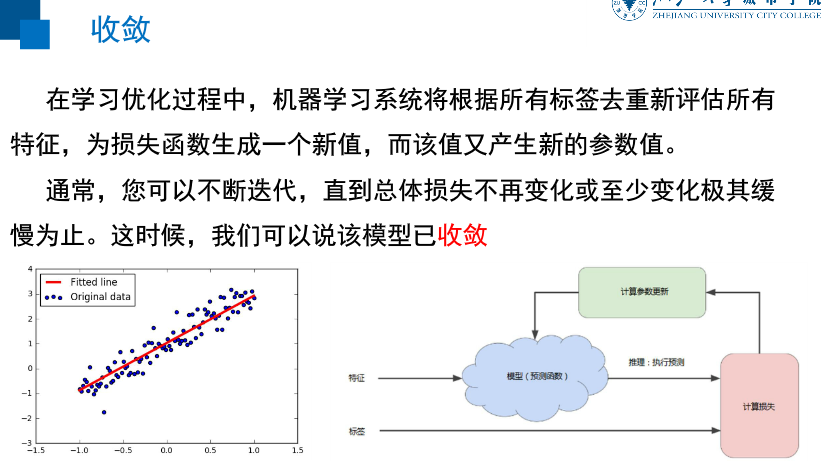
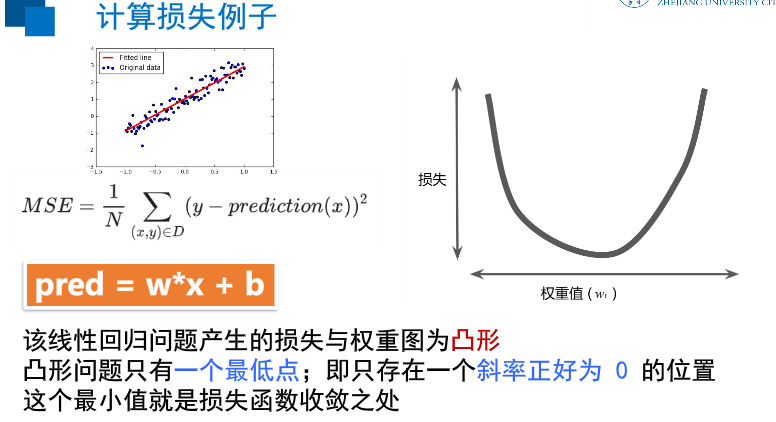
　　检查多个样本并尝试找出可最大限度地减少损失的模型

　　这一过程称为经验风险最小化

 

术语：损失

·　　损失是对糟糕预测的惩罚：损失是一个数值，表示对于单个样本而言模型

预测的准确程度

　　如果模型的预测完全准确，则损失为0，否则损失会较大

　　训练模型的目标是从所有样本中找到一组平均损失"较小"的权重和偏差

 

　　　　　　　　　　　　　　模型训练与降低损失

 

 

 

使用TensorFlow进行算法设计与训练的核心步骤

1，准备数据
2，构建模型
3，训练模型
4，进行预测

 

 

人工数据集生成

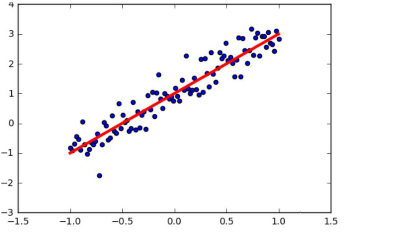
import matplotlib.pyplot as plt #载入matplotlib
import numpy as np 
import tensorflow as tf
#设置随机数种子
np.random.seed(5)
#直接采用np生成等差数列的方法，生成100个点，每个点的取值在-1,1之间
x_data=np.linspace(-1,1,100)
#y=2*x+1+噪声，其中，噪声的维度与x_data一致
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4
#画出随机生成的散点图
plt.scatter(x_data,y_data)
#画出我们想要学习到的线性函数y=2*x+1
plt.plot(x_data,2*x_data+1.0,color='red',linewidth=3)
plt.show()

                                                                 构建模型

 

import matplotlib.pyplot as plt 
import numpy as np 
import tensorflow as tf 
'''
使用TensorFlow进行算法设计与训练的核心步骤
    1，准备数据
    2，构建模型
    3，训练模型
    4，进行预测
'''
#构建模型
#定义训练数据的占位符，x是特征值，y是标签值
x_data=np.linspace(-1,1,100)
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4
#定义训练数据的占位符，x是特征值，y是标签值
x=tf.placeholder("float",name="x")
y=tf.placeholder("float",name="y")

#定义模型函数
def model(x,w,b):
    return tf.multiply(x,w)+b

 

 

 

#创建变量
'''
TensorFlow变量的声明函数是tf.Variable
tf.Variable的作用是保存和更新参数
变量的初始值可以是随机数，常数，或是通过其他变量的初始值计算得到
'''

#构建线性函数的斜率，变量w
w=tf.Variable(1.0,name="w0")

#构建线性函数的截距,变量b
b=tf.Variable(0.0,name="b0")

#pred是预测值，前向计算
pred=model(x,w,b)

设置训练参数

 

#迭代次数(训练轮数)
train_epochs=10

#学习率
learning_rate=0.05

 

 

 

定义损失函数

 

 

'''
定义损失函数
损失函数用于描述预测值与真实值之间的误差，从而指导模型收敛方向
常见损失函数:均方差（Mean Square Error,MSE）和交叉谪
'''
#采用均方差作为损失函数
loss_function=tf.reduce_mean(tf.square(y-pred))

 

 

 

定义优化器

'''
定义优化器Optimizer,初始化一个GradientDescentOptimizer
设置学习率和优化目标:最小化损失
'''

#梯度下降优化器
optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

 

 

 

创建会话

 

#声明会话
sess=tf.Session()

#变量初始化
#在真正执行计算之前，需将所有变量初始化
#通过tf.global_variables_initializer函数可实现对所有变量的初始化
init=tf.global_variables_initializer()
sess.run(init)

 

 

 

 

迭代训练

 

结果可视化

利用模型 进行预测

小结

 

源码

import matplotlib.pyplot as plt 
import numpy as np 
import tensorflow as tf 
'''
使用TensorFlow进行算法设计与训练的核心步骤
    1，准备数据
    2，构建模型
    3，训练模型
    4，进行预测
'''
#构建模型
#定义训练数据的占位符，x是特征值，y是标签值
x_data=np.linspace(-1,1,100)
y_data=2*x_data+1.0+np.random.randn(*x_data.shape)*0.4
#定义训练数据的占位符，x是特征值，y是标签值
x=tf.placeholder("float",name="x")
y=tf.placeholder("float",name="y")

#定义模型函数
def model(x,w,b):
    return tf.multiply(x,w)+b

#创建变量
'''
TensorFlow变量的声明函数是tf.Variable
tf.Variable的作用是保存和更新参数
变量的初始值可以是随机数，常数，或是通过其他变量的初始值计算得到
'''

#构建线性函数的斜率，变量w
w=tf.Variable(1.0,name="w0")

#构建线性函数的截距,变量b
b=tf.Variable(0.0,name="b0")

#pred是预测值，前向计算
pred=model(x,w,b)

#设置训练参数

#迭代次数(训练轮数)
train_epochs=10

#学习率
learning_rate=0.05

'''
定义损失函数
损失函数用于描述预测值与真实值之间的误差，从而指导模型收敛方向
常见损失函数:均方差（Mean Square Error,MSE）和交叉谪
'''
#采用均方差作为损失函数
loss_function=tf.reduce_mean(tf.square(y-pred))

'''
定义优化器Optimizer,初始化一个GradientDescentOptimizer
设置学习率和优化目标:最小化损失
'''

#梯度下降优化器
optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

#声明会话
sess=tf.Session()

#变量初始化
#在真正执行计算之前，需将所有变量初始化
#通过tf.global_variables_initializer函数可实现对所有变量的初始化
init=tf.global_variables_initializer()
sess.run(init)

#迭代训练

#开始训练
for epoch in range(train_epochs):
    for xs,ys in zip(x_data,y_data):
        loss=sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
    b0temp=b.eval(session=sess)
    w0temp=w.eval(session=sess)
    plt.plot(x_data,w0temp*x_data+b0temp)#画图
plt.show()

#当训练完成后，打印查看参数
print("w:",sess.run(w))#w的值应该在2附近
print("b:",sess.run(b))#b的值应该在1附近

#结果可视化
plt.scatter(x_data,y_data,label='Original data')
plt.plot(x_data,x_data*sess.run(w)+sess.run(b),label='Fitted line',color='r',linewidth=3)
plt.legend(loc=2)#通过参数loc指定图例位置

#利用模型进行预测
x_test=3.21

predict=sess.run(pred,feed_dict={x:x_test})
print("预测值:%f"%predict)

target=2*x_test+1.0
print("目标值:%f"%target)