Pat练习--1003 我要通过

题目

“答案正确”是自动判题系统给出的最令人欢喜的回复。本题属于 PAT 的“答案正确”大派送 —— 只要读入的字符串满足下列条件，系统就输出“答案正确”，否则输出“答案错误”。

得到“答案正确”的条件是：

1. 字符串中必须仅有 P、 A、 T这三种字符，不可以包含其它字符；
2. 任意形如 xPATx 的字符串都可以获得“答案正确”，其中 x 或者是空字符串，或者是仅由字母 A 组成的字符串；
3. 如果 aPbTc 是正确的，那么 aPbATca 也是正确的，其中 a、 b、 c 均或者是空字符串，或者是仅由字母 A 组成的字符串。

现在就请你为 PAT 写一个自动裁判程序，判定哪些字符串是可以获得“答案正确”的。

输入格式：

每个测试输入包含 1 个测试用例。第 1 行给出一个正整数 n (≤10)，是需要检测的字符串个数。接下来每个字符串占一行，字符串长度不超过 100，且不包含空格。

输出格式：

每个字符串的检测结果占一行，如果该字符串可以获得“答案正确”，则输出 YES，否则输出 NO。

 

输入样例：
10
PAT
PAAT
AAPATAA
AAPAATAAAA
xPATx
PT
Whatever
APAAATAA
APT
APATTAA
结尾无空行
输出样例：
YES
YES
YES
YES
NO
NO
NO
NO
NO
NO
结尾无空行

 

 

先分析一下3个条件

1：包含PAT这3个字符，不可以有其他的SDAD什么的等等

2：也就是说PAT、APATA、AAAPATAAA、n*APATn*A都是正确的

3： aPbTc 与aPbATca 都是正确的 ，来看看 如果把PT作为分段的

也就是 aP b Tc ~~aP bA Tca其实是等价的

因为这里是字符串，那么看到最后的c 和ca ，想想有没有可能有倍数关系

那么有 a、b、c要么为空 要么为n*A

再结合例子的正确答案来看

P前面称为a段、PT之间称为b段、T后面称为c段

也就是b段的长度乘以a段所表示的n*A应该是和后面的c段相等

也就是：

c = len(b)*a 

 

我们可以利用这个推论进行数据匹配，那么用正则是最好的方法

正则的定义：

这里需要用到：

*表示前一个字符的0次或者无限次扩展

+前一个字符的一次或无限次扩展

 

匹配规则也就是 A*PA+TA*

.表示任何单个字符
[ ] 字符集，对单个字符给出取值范围 [abc]表示a,b,c [a-z]表示a到z的所有单个字符

[^] 非字符集，对单个字符给出排除范围 [^abc]表示非a或b或c的单个字符

* 前一个字符的零次或无限次扩展 abc*表示ab,abc,abcc,abccc等

+ 前一个字符的一次或无限次扩展 abc+表示abc,abcc,abccc等

？ 前一个字符零次或一次扩展 abc?表示ab,abc

| 左右表达式任意一个 abc|def表示abc,def

{m} 扩展前一个字符m次 ab{2}c表示abbc

{m,n} 扩展前一个字符m至n次（含n次） ab{1,2}表示abc,abbc

^ 匹配字符串开头 ^abc表示abc且在一个字符串的开头

$ 匹配字符串结尾 abc$表示abc且在一个字符串的结尾


() 分组标记，内部只能使用|操作符 (abc)表示abc,(abc|def)表示abc,def

\d 数字，等价于[0-9]

然后需要用PT分片也就是 | [P|T]

split分割方法

re.split分割和一般的split还不一样

re.split(pattern, string[, maxsplit=0, flags=0])

pattern:匹配的字符串
string:需要切分的字符串
maxsplit:分隔次数，默认为0(即不限次数)
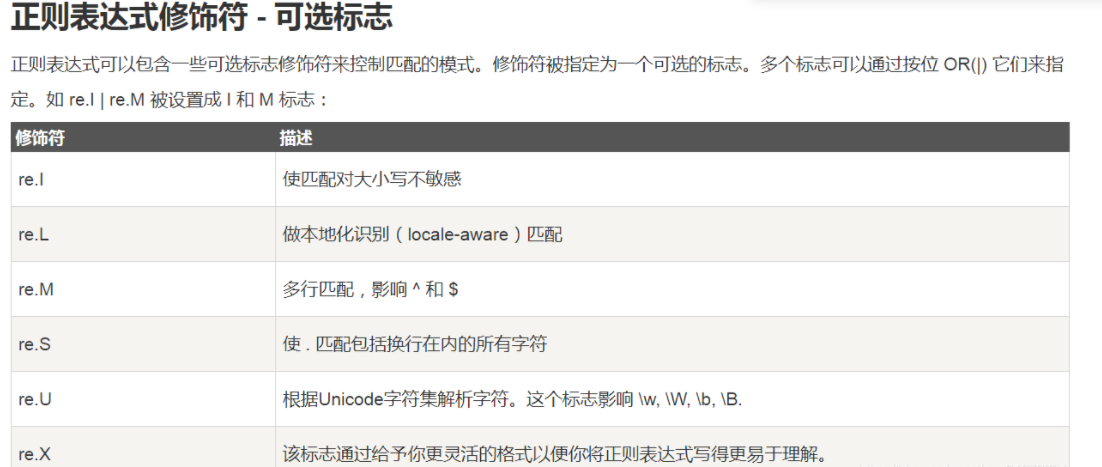
flags:标志位，用于控制正则表达式的匹配方式，比如：是否区分大小写，多行匹配等

 

 

而一般的split则是

str.split(str="", num=string.count(str))

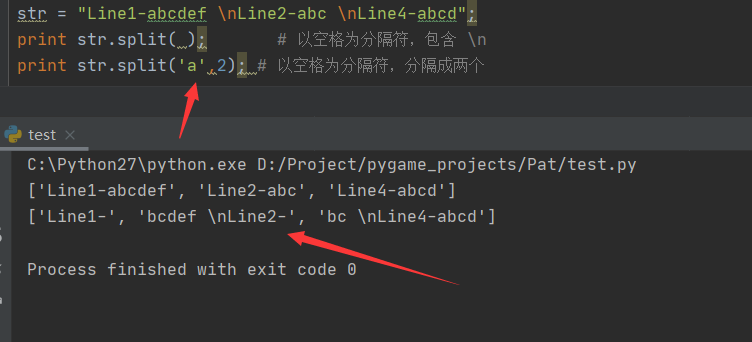
str = "Line1-abcdef \nLine2-abc \nLine4-abcd"
print str.split( ) # 以空格为分隔符，包含 \n 
print str.split(' ', 1 ) # 以空格为分隔符，分隔成两个

• str -- 分隔符，默认为所有的空字符，包括空格、换行(\n)、制表符(\t)等。
• num -- 分割次数。默认为 -1, 即分隔所有。

这里以a为分割符 分割2次

 

 所以代码是：

import re


def check(n):
    s = list()
    for i in range(0, n):
        s.append(input())
    for i in range(0, n):
        if re.match(r'A*PA+TA*', s[i]):
            # 根据推论来写正则匹配
            a = re.split(r'[P|T]', s[i])
            # 通过split 以PT来分割 也就会被分割成3份
            # a段 b段 c段
            if a[2] == a[0] * len(a[1]):
                print('YES')
            else:
                print('NO')
        else:
            print('NO')


if __name__ == '__main__':
    n = int(input())
    check(n)