数据流中的中位数

 /**

 * Problem Statement

 

Design a class to calculate the median of a number stream. The class should have the following two methods:

 

* insertNum(int num): stores the number in the class

* findMedian(): returns the median of all numbers inserted in the class

 

If the count of numbers inserted in the class is even, the median will be the average of the middle two numbers.

 

Example

 

1. insertNum(3)

2. insertNum(1)

3. findMedian() -> output: 2

4. insertNum(5)

5. findMedian() -> output: 3

6. insertNum(4)

7. findMedian() -> output: 3.5

 

 * 

 * 

* */

 

也是leetcode中的一道题《剑指 Offer 41. 数据流中的中位数》

 

暴力解决

最先想到的暴力解法：

class MedianFinder(object):

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.l = []

    def addNum(self, num):
        """
        :type num: int
        :rtype: None
        """
        self.l.append(num)
        self.l.sort()

    def findMedian(self):
        """
        :rtype: float
        """
        length = len(self.l)

        if length%2 == 1:
            return self.l[length/2]
        else:
            return float((self.l[length/2] + self.l[length/2-1]))/2.0
 

说明：

对输入元素进行排序，然后取出，如果用冒泡的话是O(n2) 如果是快排O(NlogN)

可以解决：

可以解决，但是不是最优解

 

 

堆

这道题最优解使用两个堆

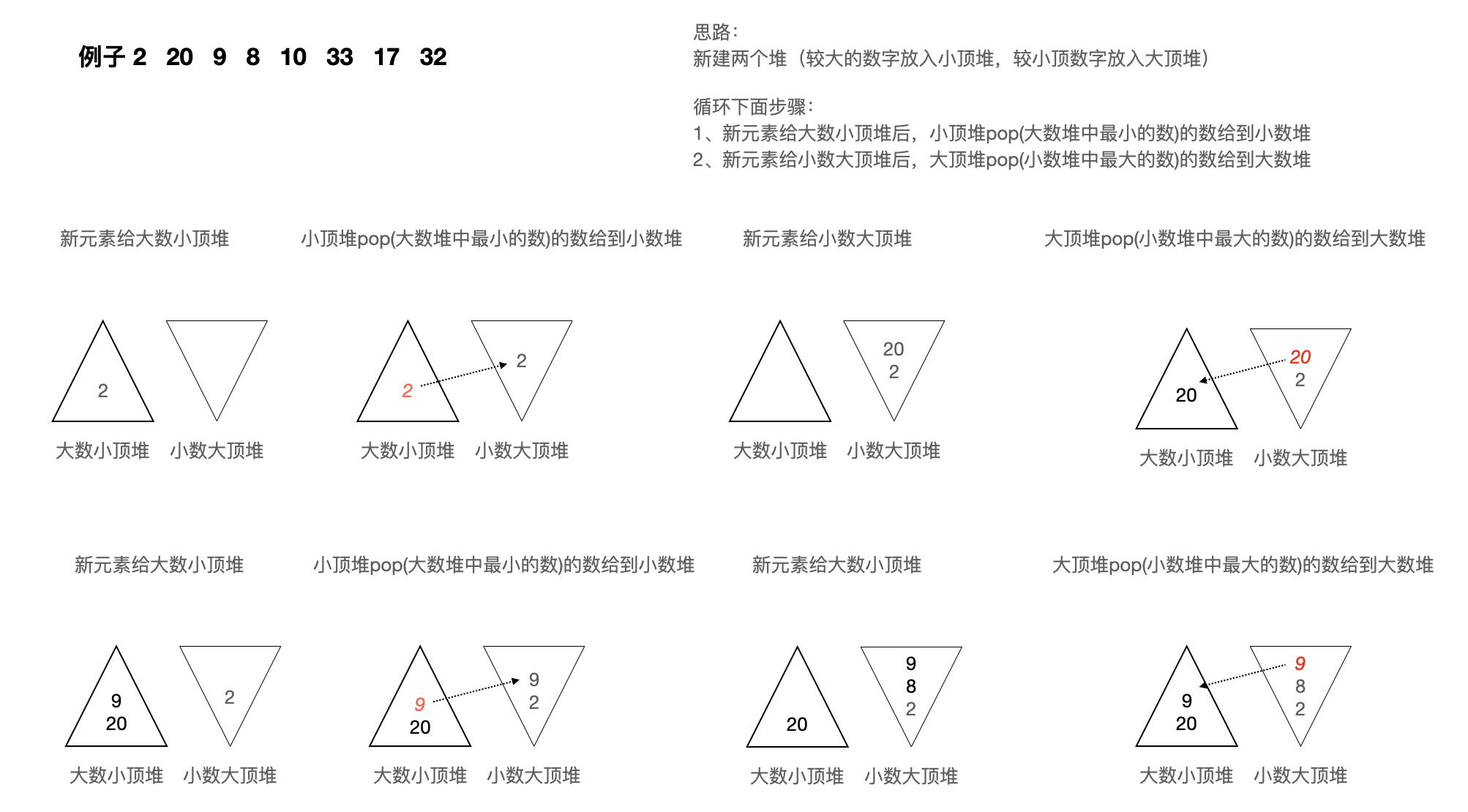
新建两个堆（较大的数字放入小顶堆，较小顶数字放入大顶堆） 

然后循环下面步骤：

1、新元素给大数小顶堆后，小顶堆pop(大数堆中最小的数)的数给到小数堆 

2、新元素给小数大顶堆后，大顶堆pop(小数堆中最大的数)的数给到大数堆

这里画了一个示意图：

from heapq import *

class MedianFinder:
    def __init__(self):
        self.A = [] # 大数小顶堆，存放较大的一半
        self.B = [] # 小数大顶堆，存放较小的一半

    def addNum(self, num: int):
        if len(self.A) != len(self.B):
            heappush(self.B, -heappushpop(self.A, num))
        else:
            heappush(self.A, -heappushpop(self.B, -num))

    def findMedian(self):
        return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0

这里需要注意，因为python只有小顶堆

因此当我们使用大顶堆的时候，只需要将数字 ✖️ -1 即可，例如之前 1 2 3，变换后 -3 -2 -1，pop的时候再  ✖️ -1 恢复即可