决策树（decision tree）

◆版权声明：本文出自胖喵~的博客，转载必须注明出处。

   转载请注明出处：https://www.cnblogs.com/by-dream/p/10088976.html

 

前言

之前在测试建模分析中讲过决策树的概念，这里要说的机器学习的决策树在构建上和最终目的与之前的决策树是有一些不同的，但是同时他们又有很多的相似性，具体可以往下看。
机器学习可以分为四大块：
　　classification (分类)，
　　regression (回归),
　　clustering (聚类),
　　dimensionality reduction (降维)

前面我们已经讲过利用最小二乘解决线性回归的问题，而这里讲的决策树是可以解决分类的问题。

 

使用场景

这里举个实际的例子来说明决策树的使用场景。
例如中关村某商家记录了之前消费者购买电脑的记录，如下：

ID	年龄	收入	学生	芝麻信誉等级	最终是否买了电脑
1	年轻	高	否	低	否
2	年轻	高	否	高	否
3	中年	高	否	低	是
4	老年	中	否	低	是
5	老年	低	是	低	是
6	老年	低	是	好	否
7	中年	低	是	好	是
8	年轻	中	否	低	否
9	年轻	低	是	低	是
10	老年	中	是	低	是
11	年轻	中	是	好	是
12	中年	中	否	好	是
13	中年	高	是	低	是
14	老年	中	否	好	否

这里他已经有了一些历史的数据，他希望根据这些历史的数据来预测当有一个人已经他的一些基本情况，能否预测出他是否要买电脑。假如我们根据之前的经验画出了这个决策数。如下：

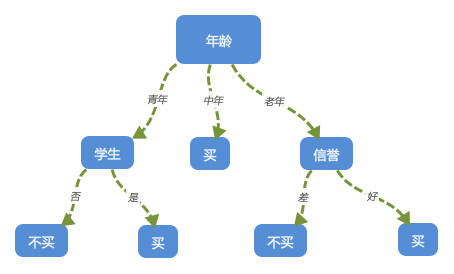
当然这个是我们自己凭感觉去画的这颗决策树，但是也算是一颗比较完整的决策树了，当有一个新的用户来了后，我们就可以按照上面划分，从跟节点一直遍历到子节点，最终到达叶子节点最底端，从而得到结论。看到这里有些人可能就会有疑问了，那么我究竟应该怎么选取跟节点呢？也就是说，我第一步究竟用“年龄”“收入”或者其他条件哪个做为跟节点先进行分离的话，我构造的决策树越简单明了呢？ 往下看

 

信息增益

前面我们介绍过信息熵（entropy）的概念，信息熵大小代表信息的不确定的大小，信息熵越大，信息不确定性越高，信息熵越小，不确定性越小。

这里我们就用这个概念来决定使用哪个条件作为我们的跟节点，具体的思路是：首先根据已有的数据算出用户是否会购买电脑的信息熵，然后加入一个条件，例如年龄，计算出不同年龄的人购买电脑的信息熵，然后用之前的信息熵减去这个信息熵，这里得到的差值的意义是：年龄这个条件的引入带来的信息混乱程度的大小。这里我们需要思考下，我们首选的跟节点肯定希望是划分之后，能够非常明显的区分开这两类东西，而非常明显的区分开也就是分开之后信息熵需要变小，那么我们就需要寻找一个目前这几个条件中对信息混乱程度影响最大的那一个。这个差值就叫做信息增益，而我们的目的其实就是找到信息增益最大的那一个。

$信息增益_{年龄} = Info - Info_{年龄}  $ 

上式中的Info代表的就是信息熵。这里我们实际计算一下年龄的信息增益。首先购买电脑的信息熵是（上面一共14个人，9个人买了，5个人没买）：

$Info = -\sum\limits_{i=1}^{n} P(X_{i})\log_{2}P(X_{i} ) = -\frac{9}{14}\log_{2}\frac{9}{14} - \frac{5}{14}\log_{2}\frac{5}{14} = 0.940bits$

不同年龄下的信息熵（5个年轻人中2个买3个不买，4个中年人都买，5个老年人3个买2个不买）是：

$Info_{年龄} = \frac{5}{14}(-\frac{2}{5}\log_{2}\frac{2}{5}-\frac{3}{5}\log_{2}\frac{3}{5})+\frac{4}{14}(-\frac{4}{4}\log_{2}\frac{4}{4} - \frac{0}{4}\log_{2}\frac{0}{4})+\frac{5}{14}(-\frac{3}{5}\log_{2}\frac{3}{5} - \frac{2}{5}\log_{2}\frac{2}{5}) = 0.694bits$

以此类推我们算出其他几个条件的信息增益为：Gain(收入)=0.029  Gain(学生)=0.151  Gain(信誉)=0.048$

因此根据按照信息增益最大进行分裂，我们就选择了年龄来做为跟节点进行划分。

连续型变量

有些细心的人可能已经发现，这里我的所有的条件（其实应该叫features）都是可以枚举的，也就是有限的，但实际过程中其实像年龄这样的字段很有可能是17、18、20、26等这样的值，那么这种情况下，我们肯定不能在划分决策树的时候将所有的年龄都当作一个分枝来划分开，这样的话就会过拟合。因此我们需要选一些关键的分割点将年龄划分开，那么这个又是怎么划分的呢？其实也是求信息熵，具体就是我们需要找到一个分割点m，当m点的信息熵比m+1和m-1两边的信息熵都小的时候我们就将这个点做为切分点来划分。通常做法可能是通过二分法来找这个点。求熵的过程我这里就不再赘述了。

 

构造决策树

其实通过前面的讲述，我们已经基本掌握了如何去构造一颗决策树，这里我再列一下这个过程：

1、所有记录看作一个节点；
2、遍历每种特征的分隔方式，找到最好的分隔点；
3、将数据分隔为两个节点部分N1和N2；
4、对N1和N2分别继续执行2-3步，直到每个节点中的项满足停止条件：

决策树算法的停止条件：

1、当每个子节点只有一种类型的时候停止构建；
2、当前节点中记录数小于某个阀值，同时迭代次数达到给定值时，停止构建过程；

我们在实际构造决策树的过程中很容易造成树枝过多，过拟合的问题。比如上面提到的第一停止的方法。一般会采取剪枝法对生成的决策树进行剪枝。剪枝分为“前剪枝”和“后剪枝”。前剪枝是在决策树构造的时候就开始进行，例如上面提到的第二种停止的方法，后剪枝是在决策树生成完成之后进行的剪枝，具体这里也先暂时不展开讨论了，有兴趣的同学可以再查阅相关的资料。

常见的决策树模型有：ID3、C4.5、CART。其实我们上面讲到的利用信息增益来生成决策树就是ID3模型，另外两个模型和ID3都是贪心的思路，区别就是使用的是其他条件来决定跟节点的选取，这里不敢再展开讨论了，否则感觉这篇文章写不完了。后面我可以单独再针对这两个算法看有没有时间单独再写个文章。

最后我们说一下决策树的优缺点

优点：

1、决策树算法中学习简单的决策规则建立决策树模型的过程非常容易理解；
2、决策树模型可以可视化，非常直观；
3、应用范围广，可用于分类和回归（CART），而且非常容易做多类别的分类；
4、能够处理数值型和连续的样本特征

缺点：

1、很容易在训练数据中生成复杂的树结构，造成过拟合（overfitting）。（剪枝可以缓解过拟合的负作用，常用方法是限制树的高度、叶子节点中的最少样本数量。）
2、决策树是基于启发式的贪心算法建立的，这种算法不能保证建立全局最优的决策树。（随机森林Random Forest 引入随机能缓解这个问题。）

 

代码

如果理解了上面的过程去实现一个决策树的算法代码其实并不是很难，但是这里我不打算说这个代码的事情，因为有很多优秀的三方库已经帮我们做好了这个的封装。例如scikit-learn，安装过程可以自行搜索，我这里也先不说了。我说下在程序处理过程中的一个小步骤。

one-hot编码

我们在使用三方库调用的时候，在传入参数的时候不能直接传入青年，中年这样的内容，因为机器是无法识别的，那么针对枚举这样的类型需要怎么来搞呢？特征工程中讲到我们可以将年龄划分为青年、中年、老年那么青年的表示方法就是100，中年是010，老年是001。也就是将之前是一个字段的裂变成来三个字段以0、1的形式传递给算法去进行处理。好看代码：

# -×- encoding=utf-8 -*-
from sklearn.feature_extraction import DictVectorizer
import csv
from sklearn import preprocessing
from sklearn import tree
from sklearn.externals.six import StringIO

# 从csv中将上面例子中的数据读出来
allElectronicsData = open('play.csv','rb')
reader = csv.reader(allElectronicsData)
header=reader.next()

print(header)

featureList=[]
labelList=[]

for row in reader:
    labelList.append(row[len(row)-1])
    rowDict={}
    for i in range(1,len(row)-1):
        rowDict[header[i]]=row[i]
        
    featureList.append(rowDict)
# featureList 构造出来是一个类似jsonArray的东西
print(featureList)

# 转为one-hot编码
vec = DictVectorizer()
dumpyX = vec.fit_transform(featureList).toarray()

print("dunmpyX "+ str(dumpyX) )
print("feature_name"+str(vec.get_feature_names()))

print("labelList "+ str(labelList))

#vectorize class lables
lb = preprocessing.LabelBinarizer()
dummyY = lb.fit_transform(labelList)
print("dummyY:" +str(dummyY))


# 注意这里entropy就是代表使用信息增益来构造决策树
clf = tree.DecisionTreeClassifier(criterion='entropy')
clf = clf.fit(dumpyX,dummyY) #构造决策树

# 打印构造决策树采用的参数
print("clf : "+str(clf))


# 验证数据，取一行数据，修改几个属性预测结果
oneRowX=dumpyX[0,:]
print("oneRowX: "+str(oneRowX))

newRowX = oneRowX
newRowX[0]=1
newRowX[2]=0
print("newRowX:"+str(newRowX))

predictedY = clf.predict(newRowX)
print("predictedY:"+str(predictedY))

在写本篇文章的时候，越写越发现里面的东西比较多，如果全部展开讲可能会有非常多的内容，所以很多地方都是简略带过，所以如果想了解细节知识的读者可以下来再单独研究～