Solution - AGC060B
简要题意：在 \(n \times m\) 的方格表中填入一些不超过 \(2^k-1\) 的数。考虑所有从左上角到右下角的最短路径，要求其中满足路径上数异或和为 \(0\) 的路径只有给定的 \(S\) 一条，问是否有解。
首先，变换看问题的角度：给定 \(n,m,S\)，则 \(k\) 应该存在一个最小值，使得问题有解（或总是无解），所以这其实是一个组合最值问题。那么考虑两个方面：证明和构造。
证明部分，我们要尽可能的增大 \(k\)，也就是增大所需的二进制位数。那么，考虑 \(S\) 的一个拐角，如图，红线表示 \(S\)，蓝线表示一个调整。
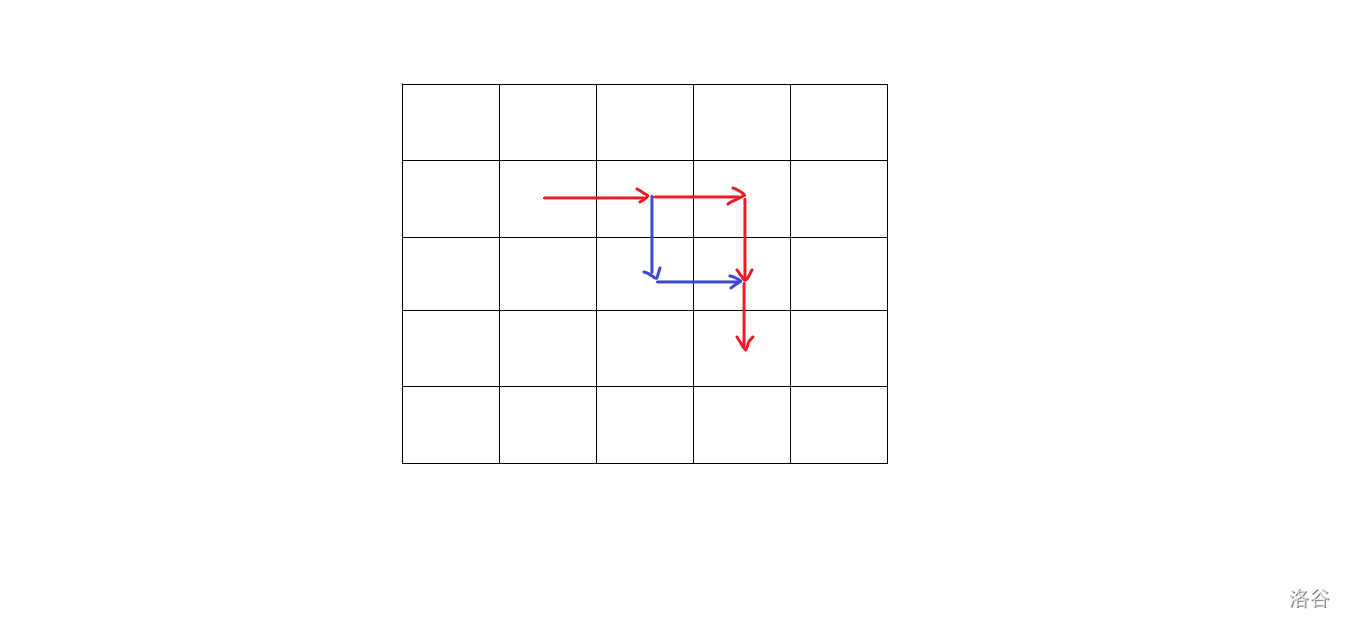
这里拐角指的是红线的拐弯处斜向相邻的这个格，即图中蓝线唯一不同与红线的格。
将红线换为蓝线之后，只改变了两个格，那么由于蓝线不能异或和为 \(0\)，所以这两个格至少有一位二进制不同。
这样的调整可以在若干个地方进行，设为 \(t\) 个，第 \(i\) 个调整会使路径的异或和改变 \(v_i\)。那么，不能有若干个 \(v_i\) 的异或和为 \(0\)，即 \(v_i\) 是一个线性无关组。由于 \(v_i\) 定义在 \(k\) 位二进制数上，所以 \(t \le k\)。
但是，并不是每个拐角都可以调整。准确地说，不是所有拐角都可以一起调整。请看下图：
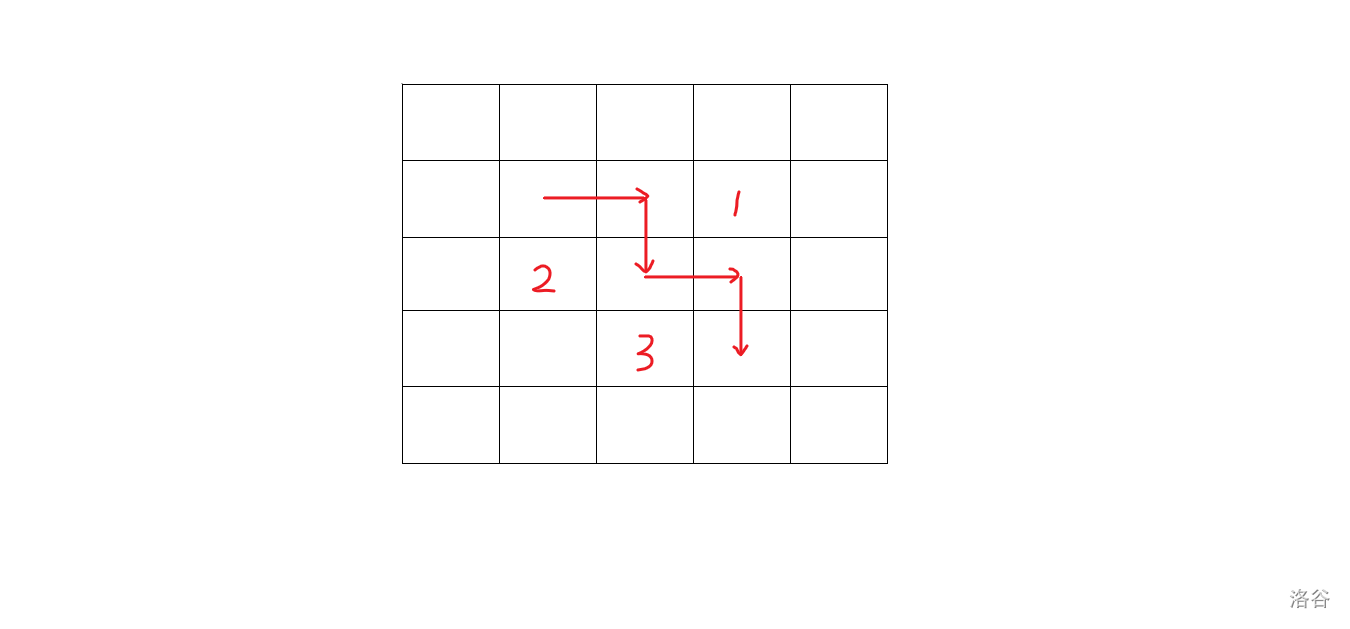
图中标出了三个拐角，但是显然不能同时做 \(1,2\) 的调整，也不能同时做 \(1,3\) 的调整。再思考一下可以发现，其实只有这样的一种情况是特殊的，也就是有一段经过两格的，连续的若干个两格只取一侧。
如此就可以算出 \(k\) 的下界，它其实就是一条路径能够经过的拐角数目的最大值，只是对于连续的两格比较特殊。
至于构造，思考到这里应该不太难了。方案如下：（想象一个人在表格中走，Ta要做一些决策）
-
对于一段长度大于等于 \(3\) 的直走，取新的一位，在这一段两端各添一个 \(1\)。这样可以使得走到这一段开头后必须走这一段结尾。
-
对于一些长度为 \(2\) 的直走，不妨设第一个 \(2\) 是竖向的，那么给每一段竖向的分配一个二进制位，在这两个格上添 \(1\)。然后取消两端由上一条添的位。
似乎说的不太清楚？上图。
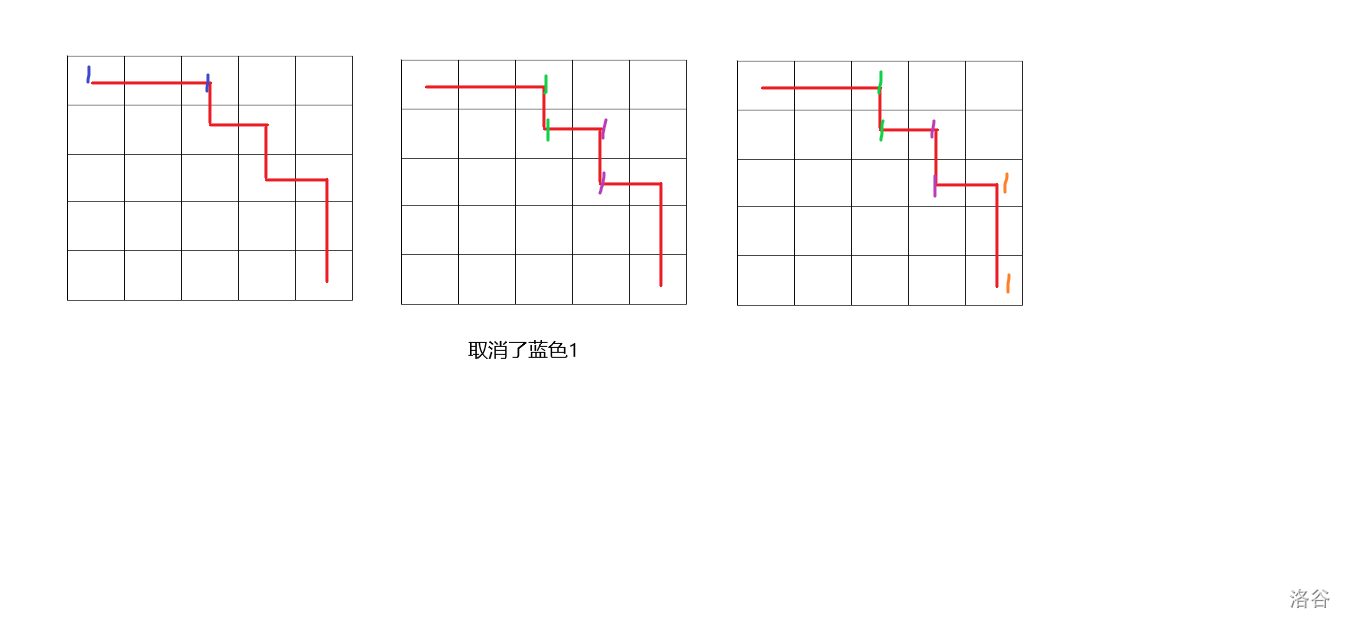
在第二条规则下，有一些“必经之路”会被挡住，所以必须要经过所有安排的 \(1\)。
容易验证这个构造确实取到了前面证明的最值。
AGC 传统，思路难，代码易。请看 Code：
#include<bits/stdc++.h>
using namespace std;
int T,n,m,k,cnt,x,y,lstx,lsty;
//x,y跟着路径S跑
//lstx,lsty表示上一个选中的拐角
char s[65];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d%d",&n,&m,&k);
scanf("%s",s+1);
cnt=0;x=y=lstx=lsty=1;
for(int i=1;i<n+m-2;i++){
if(s[i]=='D')x++;else y++;
if(s[i]!=s[i+1]){
if(s[i]=='D'&&lstx<=x-1&&lsty<=y+1)
cnt++,lstx=x-1,lsty=y+1;
if(s[i]=='R'&&lstx<=x+1&&lsty<=y-1)
cnt++,lstx=x+1,lsty=y-1;
}
}
printf(cnt<=k?"Yes\n":"No\n");
}
return 0;
}
