物理 选择性必修一 第四章 学习笔记
1.光的折射
1621年,荷兰数学家斯涅耳在分析了的大量的实验数据后,总结出光的折射定律(refraction law):折射光线与入射光线,法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦值与折射角的正弦值成正比,即 ,其中 是比例常数,它与入射角,折射角的大小有关,只与两种介质的性质有关。
光从真空中射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率(refractive index),用符号 表示。真空的折射率为 ,空气的折射率近似为 。
研究表明,一种介质的折射率,等于光在真空中的传播速度 与光在这种介质中的传播速度 之比,即 。因为光在真空中的传播速度 大于光在任何介质中的传播速度 ,因此任何介质的折射率 都大于 ,此时入射角总大于折射角。
课后习题:

-
乙和丙是可能发生的,甲和丁是不可能发生的。
-
折射角是 。光路图:
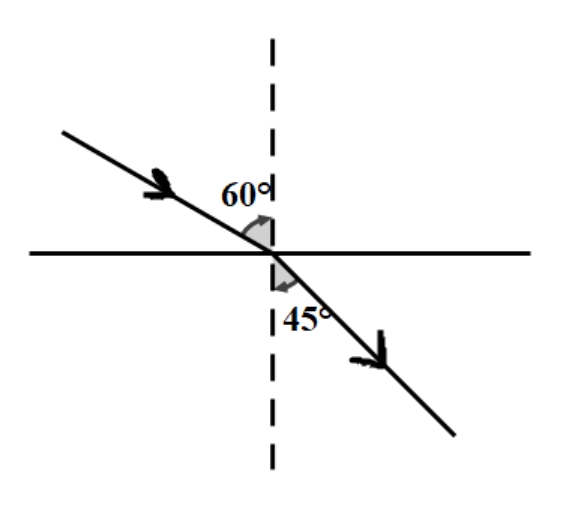
-
折射率 ,。
-
等于入射角的两倍。,能看到的角度就是 。
-
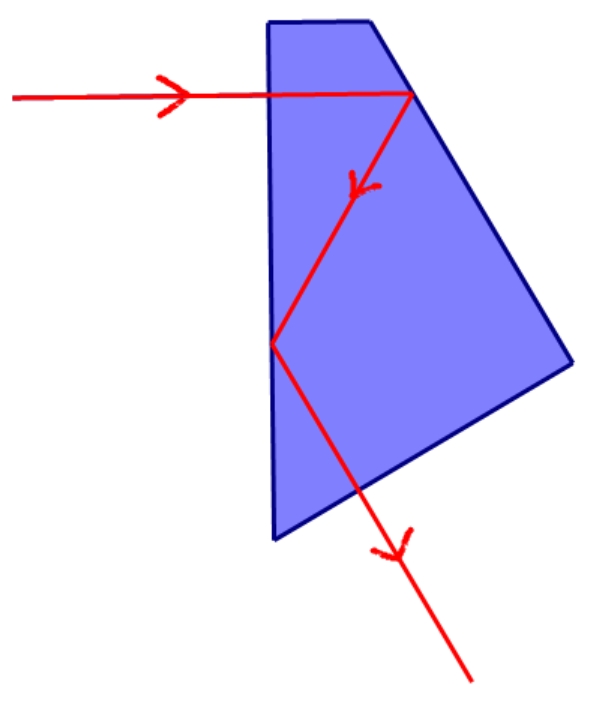
(1) 边 上的折射角等于边 上的入射角,两次折射的折射率互为倒数,所以边 上的入射角等于边 上的折射角,也就是两条光线平行。
(2) 设玻璃的厚度为定值 ,侧移 ,
可以看出, 越大,上式越大, 也就越大。
-
水中筷子发出的光线进入空气发生折射(玻璃壁可忽略),导致人观察到的实际位置发生偏移;玻璃杯相当于凸透镜,对筷子起到了放大作用,因此观察到的筷子粗一些。
2.全反射
对于折射率不同的两种介质,我们把折射率较小的称为光疏介质(optically thinner medium),折射率较大的称为光密介质(optically denser medium)。这两个概念是相对的。
当光从光密介质进入光疏介质时,同时发生折射和反射。当入射角增大到某一角度,使折射角达到 时,折射光完全消失,只剩下反射光,这种现象叫做全反射(total reflection),这时的入射角叫做临界角。入射角大于等于临界角时就会发生全反射现象。
当光在有机玻璃棒内传播时,如果从有机玻璃射向空气的入射角大于临界角,光会发生全反射,于是光在有机玻璃棒内沿着锯齿形路线传播。这就是光导纤维(optical fiber)导光的原理。实用光导纤维由内芯和外套两层组成,内芯的折射率比外套的大,光在内芯与外套的界面上发生全反射。
课后习题:
- 。
- 不能。
- 没有限制。
3.光的干涉
实验:光的双缝干涉。用激光照射金属挡板上的两条平行的狭缝,在后面的屏上观察光的干涉情况。光的干涉实验最早是英国物理学家托马斯·杨在1801年成功完成的,杨氏双缝干涉实验有力地证明了光是一种波。

光波的干涉原理和机械波的干涉是一样的。总结规律就是,当两个光源与屏上某点的距离之差等于半波长的偶数倍时,两列光波在这点相互加强,这里出现亮条纹;当两个光源与屏上某点的距离之差等于半波长的奇数倍时,两列光波在这点相互削弱,这里出现暗条纹。
通过几何计算,可以得到相邻两条亮条纹或暗条纹的中心间距约为 ,其中 是缝到屏的距离, 是两缝间距。根据这个关系式可以测出光的波长。
实验:薄膜干涉。把铁丝圈在肥皂水中蘸一下,让它挂上一层薄薄的液膜。把这层液膜当作一个平面镜,用它观察灯芯撒了食盐的酒精灯灯焰(会发出明亮的黄光)。液膜前后两个面反射的光相互叠加,发生干涉,称为薄膜干涉。因为不同颜色的光的波长不同,所以看到的亮条纹位置不同。不同颜色的光的条纹的明暗位置不同,相互交错,所以看上去会有彩色条纹。
课后习题:

- 证明了光是一种波。
- A 点为振动减弱点,B 点为振动加强点,A 听到的声音比 B 小。
- 。路程差是半波长的奇数倍,为暗条纹。
- 干涉条纹变疏。因为两个光源之间的距离变小。
5.光的衍射
实验:光的单缝衍射。用激光照射金属挡板上的一条狭缝,在后面的屏上观察光的干涉情况。可以看到,缝较宽时,光沿着直线通过狭缝,在屏上产生一条亮条纹;但当缝很窄时,亮条纹的亮度有所降低,宽度反而增大,还出现了明暗相间的条纹。
这表明光没有沿直线传播,它绕过了缝的边缘。这就是光的衍射现象。如果用白光做上述实验,得到的条纹是彩色的,这是因为不同色光的亮条纹的位置不同。
实验表明,如果增加狭缝的个数,衍射条纹的宽度将变窄,亮度将增加。光学仪器中的衍射光栅就是据此制成的,它是由许多等宽的狭缝等距离排列起来形成的光学元件。
课后习题:


6.光的偏振 激光
横波的振动方向总与波的传播方向垂直,但不同的横波即使传播方向相同,振动方向也可能是不同的。这个现象叫做“偏振现象”。
研究表明,光是一种横波。使用“偏振片”进行实验。偏振片由特定的材料制成,每个偏振片都有一个特定的方向,只有沿着这个方向振动的光波能够通过偏振片,这个方向叫做“透振方向”。事实上,只要光的振动方向不与透振方向垂直,它都可以不同程度地通过偏振片,不过强度要比振动方向与透振方向平行的光弱一些。
实验:让光束通过偏振片,在偏振片的另一侧观察。如图所示。
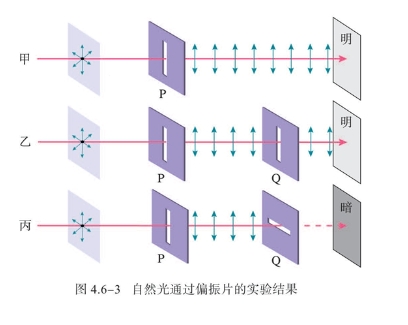
沿着特定方向振动的光叫做偏振光。通过偏振片的光波是偏振光。除了光源直接发出的光之外,我们看到的绝大多数光都是偏振光。
光是从物质的原子中发射出来的。普通的光源发出的光是完全随机的,也就是说是许多频率,相位,偏振以及传播方向各不相同的光的杂乱无章的混合。这导致两个独立的普通光源发出的光不会发生干涉。
1960年,美国物理学家梅曼率先在实验室中制造出了频率相同,相位差恒定,振动方向一致的光波,这就是激光。由于上述性质,激光具有高度的相干性,因此激光被广泛地应用于生产生活和科学研究中。
激光的另一个特点是它的平行度非常好,在传播很远的距离后仍然可以保持一定的强度。这个特点使它可以用来进行精确的测距。另外,激光的亮度很高,它可以在很小的空间和很短的时间内基中很大的能量,因此可以用激光束来切割。
课后习题:


最后的习题不写了,大部分就是一点点几何,错不了的。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具