物理 选择性必修一 第三章 学习笔记
1.波的形成
振动的传播称为波动,简称波(wave)。
我们把物体或物体的一部分在一个位置附近的往复运动称为机械振动(mechanical vibration),简称振动。(X1-2)
以抖动绳子为例,绳子是有弹性的物体,设想把一条绳子分成一个个小段,这些小段可以看作一个个相连的质点。当手握绳端上下振动时,绳端带动相邻的值点,使它也上下振动,这个质点又带动更远一些的质点……绳子上的质点都开始上下振动起来,只是后面的质点总比前面的质点迟一些开始振动。这样依次带动下去,整体上形成了凹凸相间的波形。
绳子中传播的波里,质点上下振动,波沿绳子方向(水平方向)振动。像这样质点的振动方向与波的传播方向相互垂直的波,叫做横波(transverse wave)。在横波中,凸起的最高处叫做波峰(wave crest),凹下的最低处叫做波谷(wave trough)。
对于一根长而软的弹簧,在它的一端不断推、拉弹簧,观察到弹簧圈密集的部分和稀疏的部分交替向右传播。同样,我们把一系列弹簧圈看成一系列质点。手执弹簧一端左右振动起来之后,近端的质点依次带动远端的质点左右振动,但后一个质点总比前一个质点迟一些开始振动。也就是说,后一个质点振动的相位总比前一个落后一些。这样,弹簧一端左右振动的状态就沿弹簧传播开来,整体上看就形成了疏密相间的波。
弹簧中传播的波里,质点左右振动,波向右传播。像这样质点的振动方向与波的传播方向在同一直线上的波,叫做纵波(longitudinal wave)。在纵波中,质点分布最密的位置叫做密部,质点分布最疏的位置叫做疏部。声波是一种纵波。
绳,弹簧,水,空气等是波借以传播的物质,叫做介质(medium)。组成介质的质点之间有相互作用,一个质点的振动会引起相邻质点的振动。机械振动在介质中传播,形成了机械波(mechanical wave)。
波可以传递能量,而且可以传递信息。
课后习题:

-
将石子投人平静的湖面,会激起一圈圈起伏不平的水波向周围传播。而漂浮在水面的物体上下振动却没有随波迁移。
-
(1) 8开始向上运动,12,16静止。
(2) 8到达最高点,12开始向上运动,16静止。
(3) 8回到原位置并将要向下运动,12到达最高点,16开始向上运动。
-
(1) 横波。(2) 上。
2.波的描述
对于某个固定时刻,可以建立直角坐标系描述一个波。以横波为例,横坐标 表示波的传播方向上各质点的平衡位置,纵坐标 表示某一时刻绳中各质点偏离平衡位置的位移。把平衡时位于 的质点的位移 画在 坐标平面内,得到的图象就是这一时刻波的图象,有时也称波形图。
如果波的图象是正弦曲线,这样的波叫做正弦波,也叫简谐波(simple harmonic wave)。可以证明,介质中有正弦波传播时,介质的质点在做简谐运动。请注意,简谐波的波形图与质点的振动图象虽然都是正弦曲线,但它们的意义是不同的。
在波的传播方向上,振动相位总是相同的两个相邻质点间的距离叫做波长(wavelength),通常用 表示。在横波中,两个相邻波峰或相邻波谷间的距离等于波长;在纵波中,两个相邻密部或相邻疏部间的距离等于波长。
经过一个周期 ,振动在介质中的传播距离等于一个波长 ,所以机械波在介质中传播的速度为 。因为 ,所以上式也可以写成 。机械波在介质中的传播速度由介质本身的性质决定,也受到其他因素的影响。
课后习题:
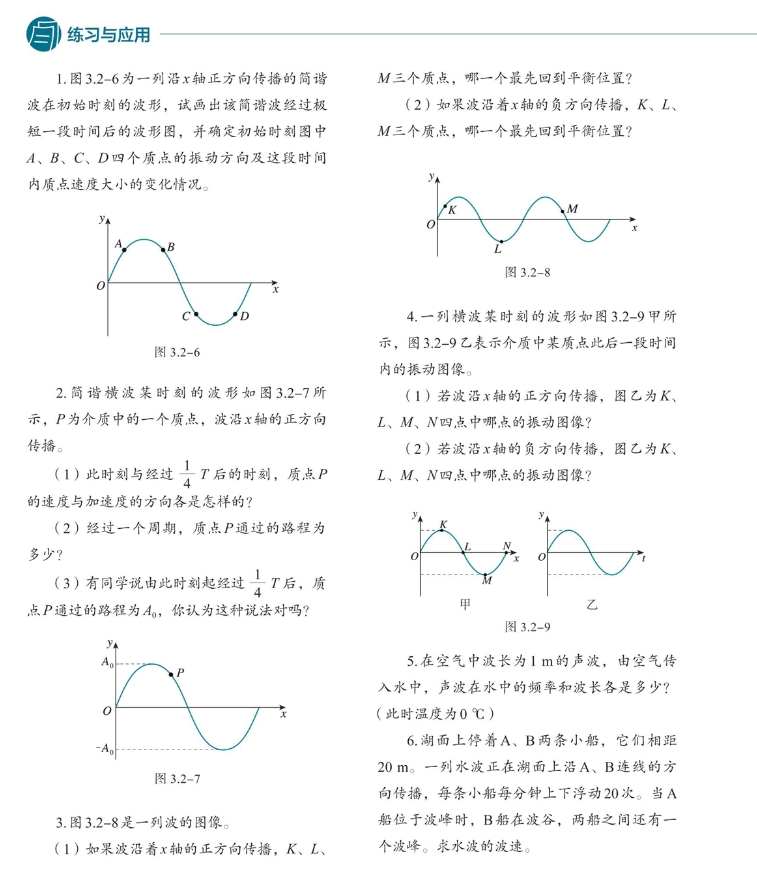
- A,D向下振动,B,C向上振动,A,C速度增大,B,D速度减小。
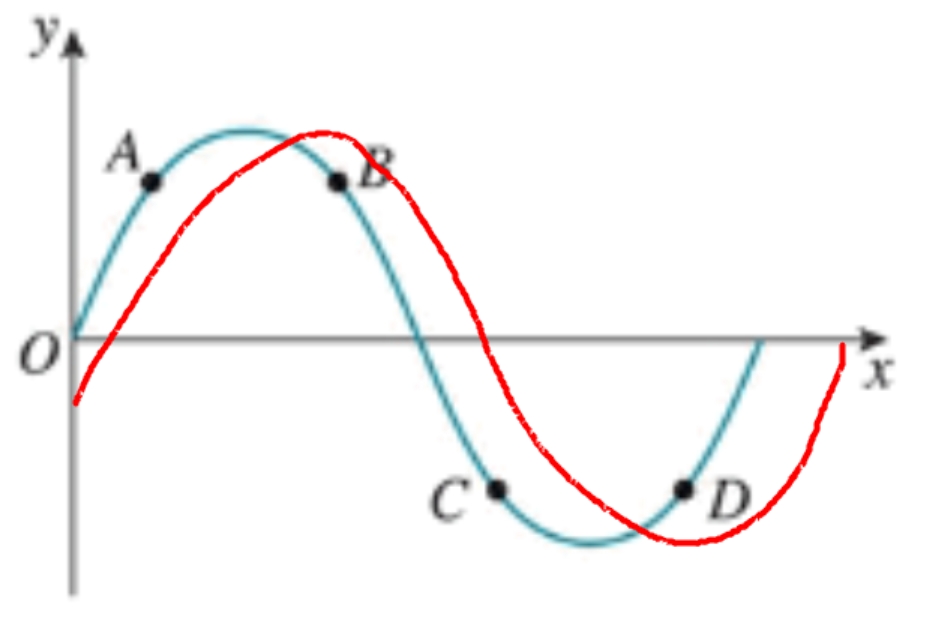
- (1) 此时刻,质点 P 速度向上,加速度向下;经过 后的时刻,质点 P 速度向下,加速度向上。(2) 经过一个周期,质点 P 通过的路程为 。(3) 不对。
- (1) K (2) M
- (1) L (2) N
- 声波从空气传入水中,频率不变,则 ,解得 。
- ,,。
3.波的反射、折射和衍射
当波遇到挡板时会发生反射(reflection)。波的反射和光的反射遵循同样的规律:反射线,法线与入射线在同一平面内,反射线与入射线分居法线两侧,反射角等于入射角。
当波从一种介质进入另一种介质时会发生折射(refraction)。
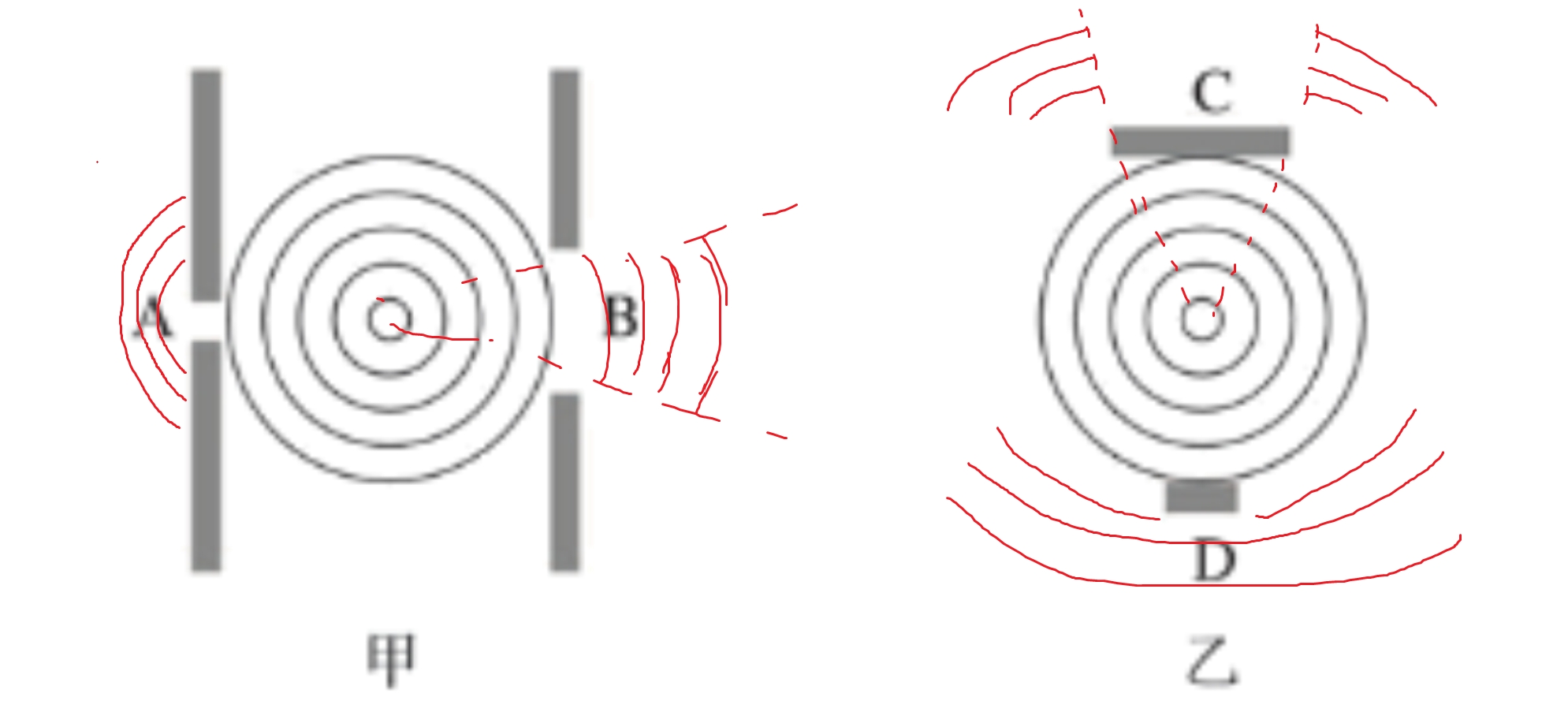
波可以绕过障碍物继续传播,这种现象叫做波的衍射(diffraction)。实验证明,只有缝、孔的宽度或障碍物的尺寸和跟波长相差不多,或者比波长更小时,才能观察到明显的衍射现象。衍射是波特有的现象。
课后习题:

- 蝙蝠发出的声波为频率较高的超声波,频率超过 。
- 高音和低音描述的是音的频率。频率高的高音波长小,衍射现象不明显,故高音减弱得明显一些。
- 可以把挡板 N 向上移动一些,减小孔的宽度,衍射现象更明显。也可以增大波的波长。
- 由于毫米级的波长比一般障碍物的尺寸小很多,不容易发生衍射现象,容易被障碍物阻挡,会给人们通过声音传播信息造成困难。
4.波的干涉
实验:在一根水平长绳的两端分别向上抖动一下,在绳上分别产生相向传播的两列波,观察两列波的传播情况。可以观察到,两列波在彼此相遇并穿过后,波的形状和相遇前一样,传播的情形也和相遇前一样。
事实表明,几列波相遇时能够保持各自的运动特征,继续传播。在它们重叠的区域里,介质的质点同时参与这几列波引起的振动,质点的位移等于这几列波单独传播时引起的位移的矢量和。
实验:水槽中,波源是固定在一个振动片上的两根细杆。振动片振动时,两根细杆周期性地触动水面,发出两个频率相同,且振动方向相同的波。可以观察到这两列波相遇后,在它们重叠的区域,水面上出现了一条条相对平静的区域和激烈振动的区域,这两列区域在水面上的位置是稳定的。如图所示。

下面来解释这样的现象:
- 如果某一时刻,两列波的波峰在某个位置相遇,也就是说两列波在这里引起的振动的相位相同,那么经过半个周期,一定是两个波谷在这里相遇。因此在这一点,两列波引起的振动总是相互加强的,质点的振幅最大。
- 如果某一时刻,两列波的波峰和波谷在某个位置,也就是说两列波在这里引起的振动的相位相反,相互削弱。而两列波的相位差是不变的,所以它们在这点引起的振动总是相互削弱的,质点的位移之和就总等于 0。
如图所示,蓝圈表示波峰,黑圈表示波谷。同色圈的交点是振动的加强区,异色圈的交点是振动的减弱区,这和实验结果是一致的。
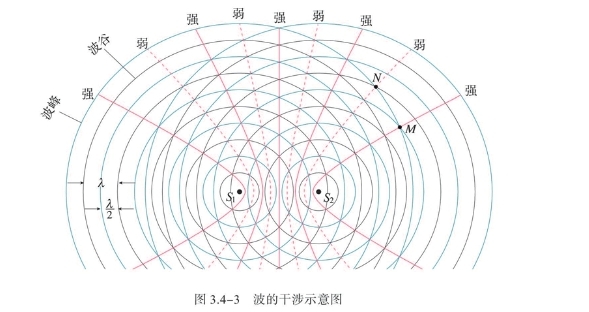
注意这个实验中,两个波源的频率、相位差和引起的振动方向都是相同的。只有这样的两列波叠加时,才会出现“某些区域的振动总是加强,某些区域的振动总是减弱”的现象,这种现象叫做波的干涉(interference)。形成的稳定图样叫做干涉图样。
一切满足上述条件的波都会发生干涉。干涉也是波特有的现象。

-
(1) M 点以两列波的振幅之和为振幅上下振动,N 点以两列波的振幅之差为振幅作上下振动。
(2) 具有最大正位移的点是两种颜色虚线(两列波波谷)的交点,具有最大负位移的点是两种颜色实线(两列波波峰)的交点。
(3) 比较“平静”的地方是所有实线与虚线的交点(波峰和波谷的交点)连成的线。
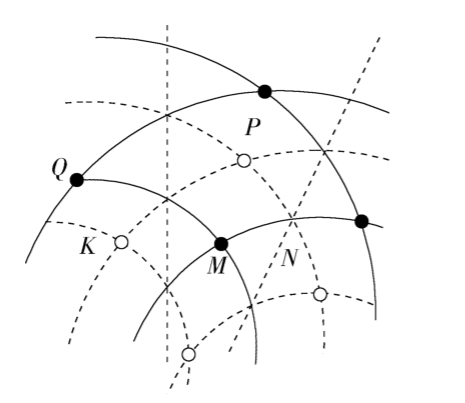
-
(1) 最高点向上(例如M向P)移动,M点没有向这个方向移动,M点垂直于纸面上下振动。
(2) 两种颜色虚线的交点是凹下最低的位置。这个位置在向上移动(例如K向N)。
(3) M质点回到平衡位置,位移为 0。
-
工作原理:如果某点到相干波源的距离差为半波长的奇数倍时,此点为振动减弱的,可以消除噪声。要达到良好的消声效果,应该让上下两束波从 a 到 b 的路程差尽可能接近半波长的某个奇数倍。
-
A,B 之间距离 A 或 的位置。
5.多普勒效应
1842年,奥地利物理学家多普勒注意到这样的现象:当不断鸣笛的车从身边疾驰而过时,鸣笛的音调听起来会由高变低。他经过研究发现,波源与观察者相互靠近或者相互远离时,接收到的波的频率都会变化。人们把这种现象称为多普勒效应(Doppler effect)。
可以这样理解声波的多普勒效应:当波源与观察者相对静止时,单位时间内通过观察者的波峰(或密部)的数目是一定的,观测到的频率等于波源振动的频率;当波源与观察者相互接近时,单位时间内通过观察者的波峰(或密部)的数目增加,观测到的频率增加;反之,当波源与观察者相互远离时,观测到的频率变小。
理论和实验都证明,光波或电磁波都有多普勒效应。
课后习题:

- 如果乙向甲移动,乙接球的时间间隔会小于 ;如果乙靠向甲的速度增大,乙接球的时间间隔会减小。
- A,C 项中波源和观察者相互接近,听到的音调变高;B,D 项中波源和观察和相互原理,听到的音调变低。
本章习题

-
-
。
-
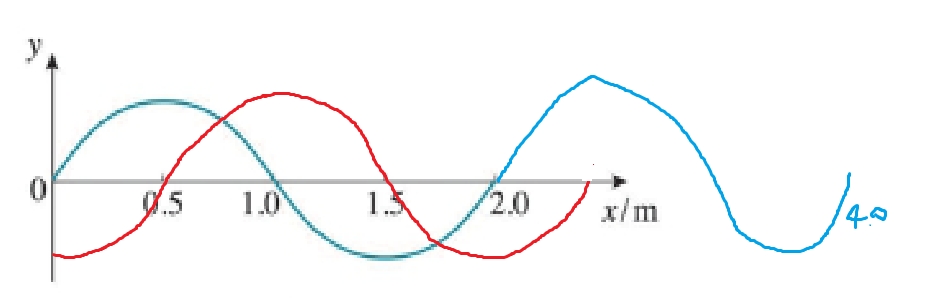
图象向右平移,然后补上开头的部分即可。 -
(1) 波长 ,振幅 。(2) 频率 ,速度 。(3) 波是向右传播的。
-
(1) ,,。(2) 。
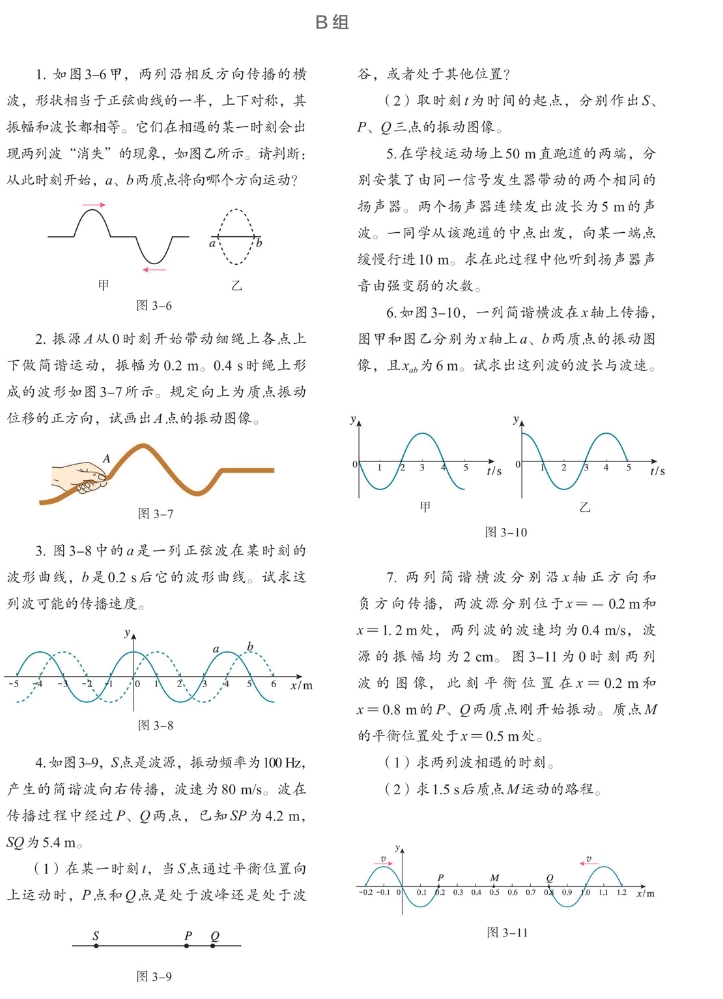
-
a 向下运动,b 向上运动。
-
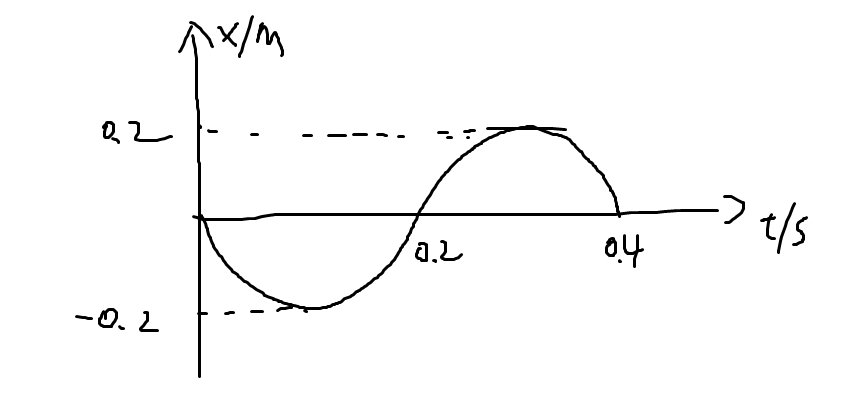
-
可能在 内移动了 , 是整数。速度 , 可以是任意整数。
-
(1) 。此时 P 处于波谷,Q 处于波峰。(2) 图略。
-
4 次。在经过距离两个波源距离差为半波长的奇数倍的位置时声音变弱。
-
周期 ,,,。
-
(1) 。 (2) 。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具