物理 选择性必修一 第二章 学习笔记

1.简谐运动

我们把物体或物体的一部分在一个位置附近的往复运动称为机械振动（mechanical vibration），简称振动。

把一个有小孔的小球连接在弹簧的一端，弹簧的另一端固定，小球套在光滑的杆上能够自由滑动。我们把小球和弹簧组成的系统称为弹簧振子（spring oscillator），有时也简称为振子。系统中当弹簧未形变时，小球所受合力为 $0$，称此时小球处于平衡位置（equilibrium position）。如图所示。

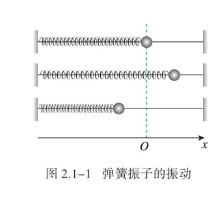
用频闪照相等方法，研究弹簧振子运动的特点。选取小球平衡位置为坐标原点，建立坐标系，得到如图所示的图象。

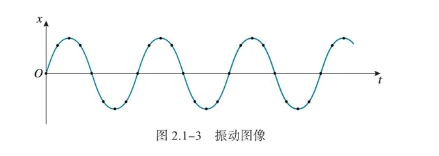
可以看出小球位移与时间的关系似乎可以用正弦函数来表示。可以用两种方案来验证，一是通过测量振幅和周期计算出函数表达式，然后取若干个位置验证；二是把一些位置的值输入计算机。

如果物体的位移与时间的关系遵从正弦函数的规律，即它的振动图像（$x-t$ 图象）是一条正弦曲线，这样的振动被称为简谐运动（simple harmonic motion）。简谐运动是最基本的振动。

课后习题：

1. 横坐标代表时间，纵坐标代表位移。匀速拖动使得时间和白纸拖动的距离成正比。横轴上应该标出每 $5\text{cm}$ $1\text s$ 的刻度。

2. (1)最大距离为 $10\text{cm}$。

   (2)$1.5\text s$ 时，质点在相对平衡位置正方向 $5\sqrt 2\text {cm}$ 的位置，向负方向移动；$2.5\text s$ 时，质点在相对平衡位置负方向 $5\sqrt 2\text {cm}$ 的位置，向负方向移动。

   (3)在 $0\sim 1,2\sim 3\text s$ 的时候相同，在 $1\sim 2,3\sim 4\text s$ 的时候相反。

   (4)位移是 $0$。

   (5)路程是 $20\text{cm}$。

2.简谐运动的描述

对于做简谐运动的物体，其位移 $x$ 与运动时间 $t$ 可以用一个一般的函数表达式刻画：

$$x=A\sin (\omega t+\varphi)$$

因为 $|\sin (\omega t+\varphi)|\le 1$，所以 $|x|\le A$，也就是说 $A$ 是物体离开平衡位置的最大距离。我们把振动物体离开平衡位置的最大距离叫做物体的振幅（amplitude）。振幅是表示振动幅度大小的物理量，常用字母 $A$ 表示，单位是米。振动物体运动的范围是振幅的两倍。

振动物体一个完整的振动过程称为全振动。做简谐运动的物体完成一次全振动所需要的时间，叫做振动的周期（period），通常用字母 $T$ 表示；物体完成全振动的次数与所用时间之比称为频率（frequency），通常用字母 $f$ 表示。则有 $f=\frac{1}{T}$。在国际单位制中，周期的单位是秒，频率的单位是赫兹（hertz），简称赫，符号是 $\text{Hz}$。$1\text{Hz}=1\text s^{-1}$。

周期和频率都是表示物体振动快慢的物理量。周期越小，频率越大，振动越快。根据正弦函数的规律，可以得到 $\omega=\frac{2\pi}{T}=2\pi f$。

通过实验可以发现，弹簧振子的振动周期与其振幅无关。这对于所有简谐运动都是成立的。

从函数中可以发现 $(\omega t+\varphi)$ 确定时 $x$ 即确定，所以物理学中将其称为相位（phase）。$\varphi$ 是 $t=0$ 时的相位，称为初相。经常用到的是两个具有相同频率的简谐运动的相位差（phase difference）。

课后习题：

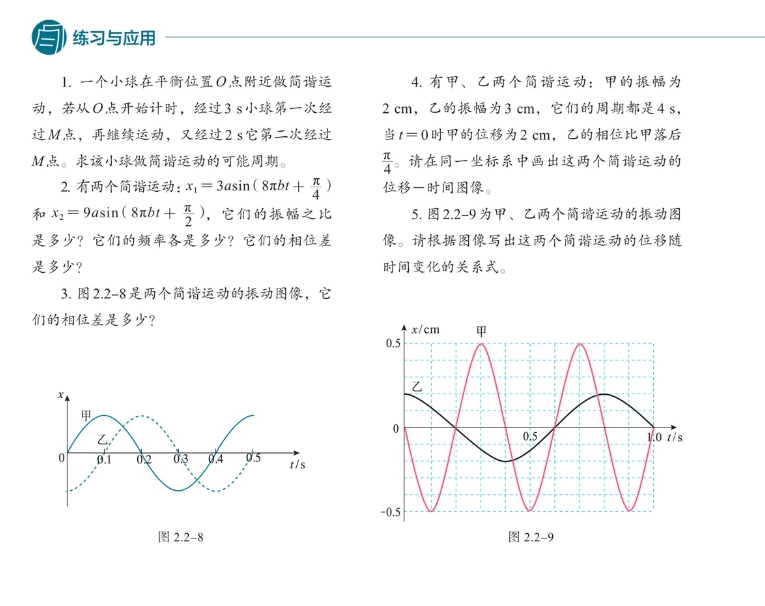
1. 如果 $M$ 点在正半轴上，可以算出周期为 $16\text s$；如果 $M$ 点在负半轴上，可以算出周期为 $\frac{16}{3}\text s$。

2. 振幅之比是 $A_1:A_2=1:3$，频率是 $f_1=f_2=\frac{1}{4b}$，相位差是 $\frac{\pi}{4}$，$x_2$ 领先。

3. 相位差是 $\frac{\pi}{2}$，实线领先。

4. 

5. $x_{甲}=0.005\sin(5\pi x+\pi),x_{乙}=0.002\sin(5\pi x+\frac{pi}{2})$

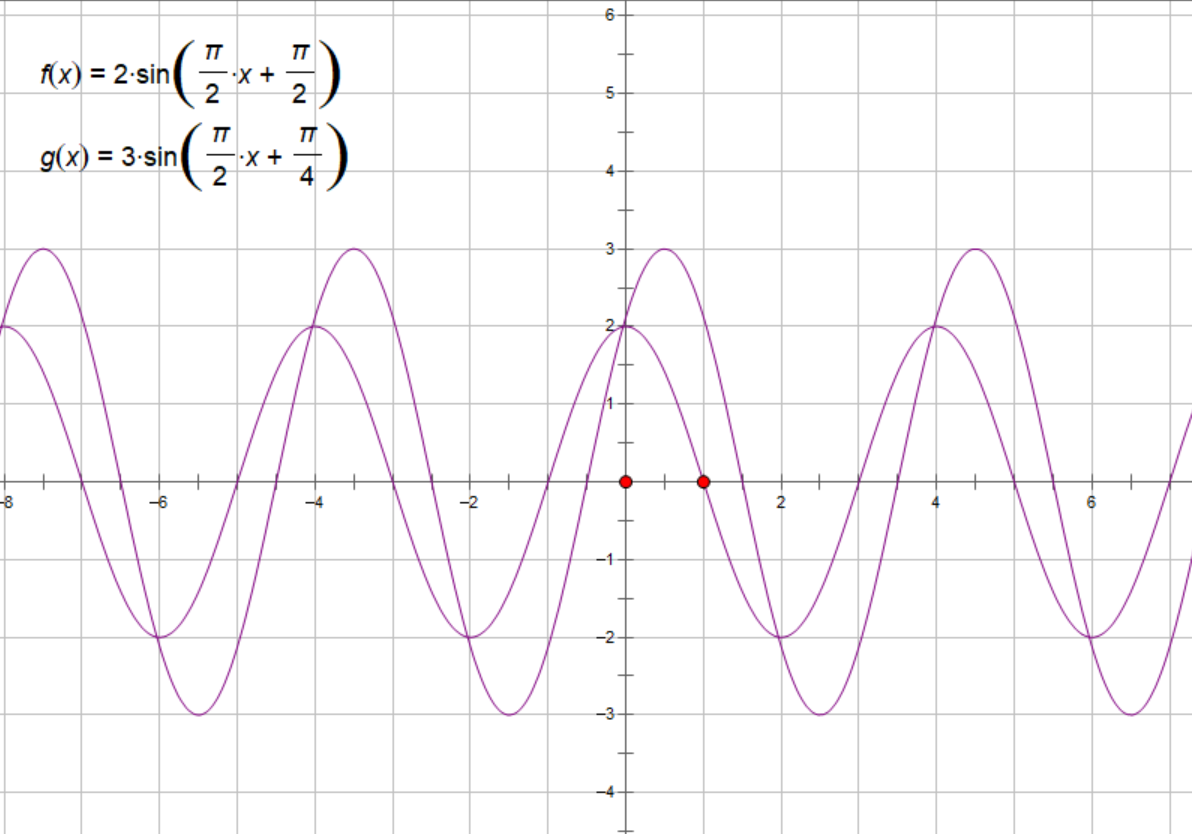
3.简谐运动的回复力和能量

我们把使物理回到平衡位置的力称为回复力。

如果物体在运动方向上所受的力与它偏离平衡位置位移的大小成正比，并且总是指向平衡位置，物体的运动就是简谐运动。

理论上可以证明，在弹簧振子运动的任何位置，系统的动能与势能之和都是一定的，遵守机械能守恒定律。

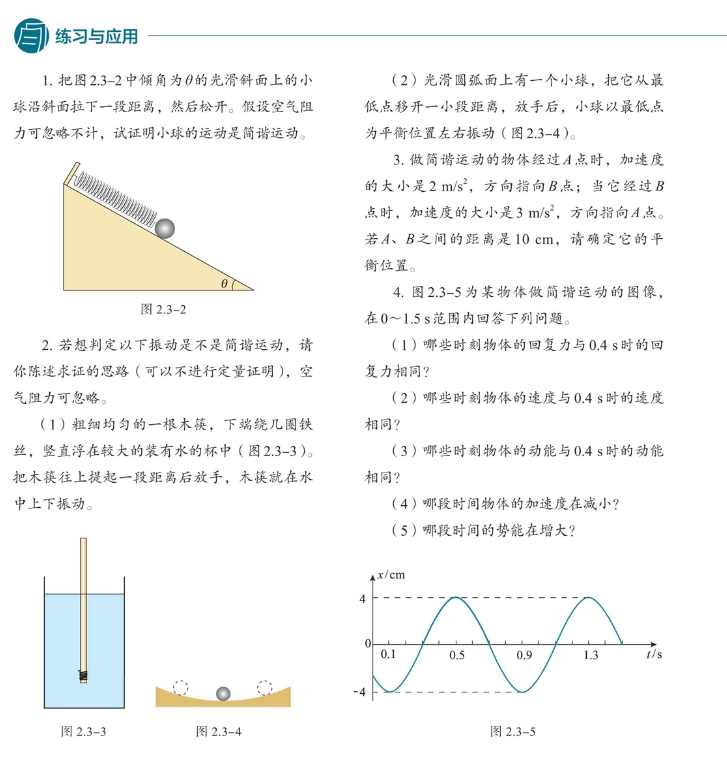
1. 只考虑沿着斜面方向的力，小球受到弹簧弹力作用和重力的一个分力作用。后者是固定的，且等于平衡位置时弹簧的弹力。而弹簧弹力的变化量与长度的变化量成正比，所以小球所受合力与它偏离平衡位置位移的大小成正比，就做简谐运动。

2. (1) $F_{浮}=\rho gV=\rho gSh$，浮力与木筷浸入水中的深度成正比。平衡位置浮力等于重力，所以合力与偏离平衡位置位移的大小成正比，做简谐运动。

   (2) 类似于单摆，是一个简谐运动。

3. 加速度正比于回复力大小，正比于位移，所以 $A,B$ 到平衡位置的距离等于加速度之比。于是平衡位置在 $A,B$ 之间，距 $A$ 有 $4\text{cm}$。

4. (1) $0.6\text s,1.2\text s,1.4\text s$。

   (2) $0.2\text s,1.0\text s,1.2\text s$。

   (3) $0\text s,0.2\text s,0.6\text s,0.8\text s,1.0\text s,1.2\text s,1.4\text s$。

   (4) $0.1\sim 0.3,0.5\sim 0.7,0.9\sim 1.1,1.3\sim 1.5\text s$。

   (5) $0\sim 0.1,0.3\sim 0.5,0.7\sim 0.9,1.1\sim 1.3\text s$。

4.单摆

将一个小球用细线悬挂起来，如果细线的长度不可改变，细线的质量与小球相比可以忽略，球的直径与线的长度相比也可以忽略，这样的装置就叫做单摆（simple pendulum）。单摆是实际摆的理想化模型。

通过分析单摆的回复力来证明这是一个简谐运动。设单摆摆长为 $l$，摆球质量为 $m$。设某一时刻摆球运动到某一位置 $P$，摆线与竖直方向的夹角为 $\theta$。则重力沿圆弧切线方向的分力 $F=mg\sin \theta$ 充当回复力。

虽然 $F$ 与位移 $x=\vec{OP}$ 并不成正比也不反向，但是当 $\theta$ 很小时，摆球运动的圆弧可以看成直线，就可以认为 $F$ 指向平衡位置 $O$，与位移 $x$ 反向。圆弧 $\overset{\frown} {OP}$ 的长度课近似认为与位移 $x$ 大小相等。于是回复力 $F=-\frac{mg}{l}\cdot x=-kx$，可见单摆在摆角很小的情况下做简谐运动。

实验表明，单摆做简谐运动的周期与摆长正相关，与摆球质量和振幅无关。进一步，可以得到如下定量关系：设摆长为 $l$，周期为 $T$，则

$$T=2\pi\sqrt{\frac{l}{g}}$$

课后习题：

1. 周期变为 $\sqrt 2 T$。

2. 摆长 $l=\frac{g}{\pi^2}=1.013\text m$。月球上周期 $T'=2\pi \sqrt{\frac{l}{g'}}=5\text s$，$50$ 次全振动所需时间 $250\text s$。

3. (1) 周期之比为 $T_{甲}:T_{乙}=1:2$，摆长之比为 $l_{甲}:l_{乙}=1:4$。

   (2) 甲摆动到了平衡位置，向左移动。

4. (1) $l=1.013\text m$。(2) $\theta = \arcsin \frac Al=2.29^{\circ}$。

6.受迫振动 共振

弹簧振子和单摆在没有外力干预的作用下做简谐运动，周期或频率与振幅无关，仅由系统自身的性质决定。我们把这种振动称为固有振动，其振动频率称为固有频率（natural frequency）。

由于实际的振动系统都会受到摩擦力，黏滞力等阻碍作用，振幅必然逐渐减小，这种振动称为阻尼振动（damped vibration）。要想产生持续的振动，最简单的办法是使周期性的外力作用于振动系统，对系统做功，补偿系统的能量损耗。这种周期性的外力叫做驱动力，系统在驱动力作用下的振动叫做受迫振动（forced vibration）。

实验表明，物体做受迫振动达到稳定后，物体振动的频率等于驱动力的频率，与物体的固有频率无关。

在周期性驱动力作用下的受迫振动，其振幅与驱动力的频率和物体固有频率相关。具体来说，驱动力的频率与物体的固有频率相差（绝对值）越小，受迫振动的振幅越大。特别地，当驱动力的频率等于物体的固有频率时，物体做受迫振动的振幅达到最大值，这种现象称为共振（resonance）。

课后习题：

1. 这是一个受迫振动，小球振动的频率与其固有频率无关，只与驱动力的频率有关。驱动力的频率等于圆盘转动的频率，为 $0.25\text{Hz}$。

2. (1) B,C 球也开始振动，且 C 球振动的振幅比较大。

   (2) A,B 球也开始振动，且 A 球振动的振幅比较大。

3. $5.33\text{m/s}$。

4. (1) $l=\frac{g}{4\pi ^2f^2}=2.76\text m$。

   (2) 摆长增大，周期增大，频率减小，横坐标左移。

5. 从 P 到 N，势能相同，动能减小，机械能减小。

本章习题

1. 速度，动能达到最大值，位移，势能，回复力，加速度达到最小值。

2. 振幅 $2\text{cm}$，周期 $0.2\text{s}$，频率 $5\text{Hz}$。

3. 一个余弦函数，后面忘了。

4. 调短摆长。使周期减小。

5. 等价于摆长为 $R$ 的单摆。频率为 $\frac{1}{2\pi}\sqrt{\frac{g}{R}}$。

6. 第一个小球耗时 $\frac{\pi}2\sqrt\frac{l}{g}$，第二个小球耗时 $\sqrt{\frac{2l}{g}}$，因为 $\frac{\pi}2\gt \sqrt 2$，所以第二个小球先到。

7. (1) 振幅是 $2\text{cm}$，周期是 $0.8\text{s}$，频率是 $1.25\text{Hz}$。

   (2) 到 G 点完成了一次全振动。

   (3) B,D,F 动能最大，A,C,E,G 势能最大。

1. 每 $10$ 次全振动损失的能量是 $mg\Delta h=0.006\text J$。$200\text s$ 内需要补充 $5$ 次能量，共 $0.03\text J$。

2. $$T_1/T_2=2\pi\sqrt\frac{l}{g_1}/2\pi\sqrt\frac{l}{g_2}=\sqrt {g_2}/\sqrt {g_1}$$
   $$g_1=\frac{km_1}{R_1^2},g_2=\frac{km_2}{R_2^2}$$
   $$T_1/T_2=R_1\sqrt {m_2}/R_2\sqrt{m_1}$$

3. (1) $l=\frac{g}{4\pi^2}\cdot T^2$，$g=\frac{y_B-y_A}{x_B-x_A}\cdot 4\pi^2=\frac{4\pi^2(l_2-l_1)}{T_2^2-T_1^2}$

   (2) 可以。因为摆球质量分布不均匀只会导致测量的摆长不准确，但摆长的变化是不受影响的，图象斜率不变。

4. (1) $x=5\sin (\frac{\pi}{2}x)$。

   (2) 加速度增大，速度减小，动能减小，弹性势能增大。

   (3) 位移是 $0$，路程是 $500\text{cm}$。

5. (1) $T=0.4\pi \text s$，$l=\frac{gT^2}{4\pi^2}=0.4\text m$。

   (2)(3) $F_B-mg=m\frac{v^2}{l}$，$mg\cos \theta=F_A$，$mgl(1-\cos\theta)=\frac12mv^2$

   解得 $m=0.05\text {kg},v=0.179\text{m/s}$。

6. 为了使筛子的振幅增大，可以增大共振筛的固有频率或者减小驱动力的频率，也就是可以减小筛子的质量或者降低电压。