笔试题总结:贪心算法(或动态规划)
概念:
当一个问题具有最优子结构性质时,可用动态规划算法,有时会有更简单有效的算法,那就是贪心算法,贪心算法是通过一系列的选择来得到问题的解,贪心算法并不从整体最优上加以考虑,所做的选择只是在某种意义上的局部最优解。但对范围相当广的许多问题能产生整体最优解。在一些情况下,即使贪心算法不能得到整体最优解,但其最终结果却是最优解的很好的近似解。
贪心算法的基本要素:
贪心选择性质:所求解的问题的整体最优解可以通过一系列局部最优的选择来,即贪心选择达到。贪心选择所依赖的是以前所做过的选择,而对以后所做的选择没有关系。
最优子结构性质:一个问题的最优解包含其子问题的最优解。
贪心算法与动态规划的区别:
动态规划是通过自底向上的方式解决子问题,贪心算法是通过自顶向下的迭代方式做出贪心选择,求解问题的最优解。两共同点是都具有最优子结构性质。
动态规划:(0-1)背包问题
https://blog.csdn.net/qq_38410730/article/details/81667885
类似:
1.欢聚时代:容量M,电影N部,每部喜爱值不一样,电影大小不一样,求不超过容量最喜欢的值
100 5//容量,5部电影
29 28 19 18 20//电影容量
9 4 3 8 10//每部喜爱值
以上是典型 的0-1背包问题,动态规划来解决
思路:
weight[N]={29 28 19 18 20}
value[N]={9 4 3 8 10}
容量N=100
| (i) | weight(j) | value |
| 0 | 0 | 0 |
| 1 | 29 | 9 |
| 2 | 28 | 4 |
| 3 | 19 | 3 |
| 4 | 18 | 8 |
| 5 | 20 | 10 |
B(i,j)//意思是,可选第i件商品以前的任意商品,还剩余容量j的最大价值
B(i,j)---->j(剩余容量)<weight[i](第i件物品的容量,重量),只能选第i-1件以前的,即b(i-1,j)
---------->选i, B(i-1,j-values[i])
---------》不选i, B(i-1,j)
动态规划:创建一个二维数组
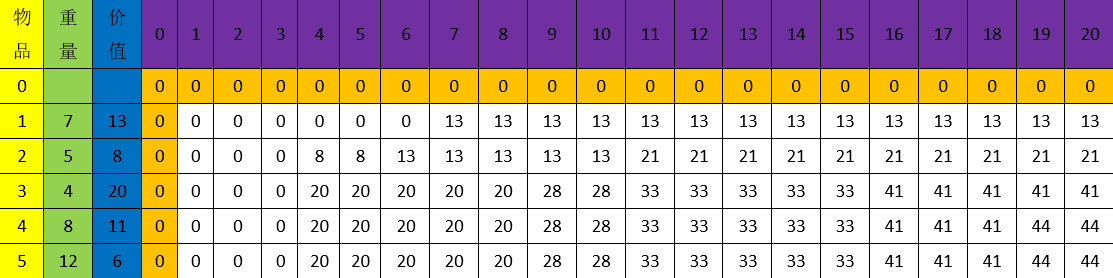
//背包问题 int dp(vector<int>& value, vector<int>& weight, int cap,int n) { vector<vector<int>> vvi(n + 1, vector<int>(cap + 1, 0)); for (int i = 1; i < n + 1;i++) { for (int j = 1; j < cap + 1;j++) { if (j < weight[i]) vvi[i][j] = vvi[i - 1][j]; else { int A = vvi[i - 1][j - weight[i]]+value[i]; int B = vvi[i - 1][j]; vvi[i][j] = max(A,B); } } } return vvi[n][cap]; } int main() { int n, cap; int v, w; cin >> n >> cap; vector<int>value(n+1,0), weght(n+1,0); for (int i = 1; i < n+1;i++) { cin >> v; value[i]=v; } for (int i = 1; i < n+1; i++) { cin >> w; weght[i]=w; } for (auto i:value) { cout << i << " "; } cout << endl; for (auto i : weght) { cout << i << " "; } cout << endl; cout << n << cap << endl; cout <<dp(value,weght,cap,n)<<endl; system("pause"); }
下面的解法是错误的
#include <iostream> #include <map> #include <vector> #include <algorithm> #include <functional> using namespace std; int main() { int cap,num,tmp; map<int, int, greater<int>> love_size; cin >> cap>>num; cout << cap << ":" << num << endl; vector<int> movie, love; for (int i = 0; i < num;i++) { cin >> tmp; movie.push_back(tmp); } for (int i = 0; i < num; i++) { cin >> tmp; love.push_back(tmp); } for (int i = 0; i < num;i++) { love_size.insert(make_pair(love[i],movie[i])); } int love_sum=0; int movie_cap = 0; for (auto v:love_size) { movie_cap += v.second; love_sum += v.first; cout << "select:" << v.first << ":" << v.second <<":"<<love_sum<<endl; if (movie_cap >= cap) { if (movie_cap> cap) love_sum -= v.first; break; } } cout << love_sum << endl; system("pause"); }
华为:一百块钱需要买100只鸡,公鸡5元一只,母鸡3元一只,小鸡一元三只。请输出所有可能的情况。
5*x+3*y+z/3=100
x+y+z=100
0=<x<=25
0=<y<=33
0=<z/3<=100
#include<iostream.h> void main() { int x,y,z,count=0; cout<<"百钱买百鸡的方案有:"<<endl; for(x=0;x<=20;x++) for(y=0;y<=33;y++) for(z=0;z<=300;z=z+3) if(5*x+3*y+z/3==100&&x+y+z==100) { ++count; cout<<count<<":"<<x<<","<<y<<","<<z<<endl; } }
类似的比如百度:

1,2
N
可以考虑使用动态规划或者斐波拉数列
F(N)=F(N-1)+F(N-1) //F表示多少中方法
n=1 return 1
n=2 return 2
return f(n-1)+f(n-2)
或者
void step(int n) { vector<long long> v(n+1, 0); if(n>=1) v[1] = 1; if(n>=2) v[2] = 2; for (int i = 3; i <= n;i++) { v[i] = v[i - 1] + v[i - 2]; } cout << v[n] << endl; } int main() { step(1); step(2); step(3); step(4); step(5); step(10); system("pause"); }
//间隔,不能选相邻的数字,使其最优(和最大)
//1 2 4 1 7 8 3
//4 1 1 9 3
//opt[i] = max(opt[i - 2] + vi[i] , opt[i-1]);
int dp_dg(vector<int>& vi,int n)//最后一个元素
{
int A, B;
if (n == 0) return vi[0];
else if (n == 1) return max(vi[0], vi[1]);
else
{
A = dp_dg(vi, n - 2) + vi[n];
B = dp_dg(vi, n - 1);
return max(A, B);
}
}
int dp(vector<int>& vi)//最后一个元素
{
int A, B;
vector<int> v_dp(vi.size(),0);
v_dp.resize(vi.size());
v_dp[0] = vi[0];
v_dp[1] = max(vi[1], vi[0]);
for (int i = 2; i < vi.size();i++)
{
A = vi[i] + v_dp[i - 2];
B = v_dp[ i - 1];
v_dp[i] = max(A,B);
}
return v_dp[v_dp.size() - 1];
}
int main()
{
int num,tmp;
cin >> num;
vector<int> vi(num);
for (int i = 0; i < num;i++)
{
cin >> tmp;
vi.push_back(tmp);
}
cout<<dp(vi)<<endl;
system("pause");
}
//3 34 4 12 5 2能否凑出9,能,返回true,否则返回false
//3 34 4 12 5 2 //s=9 true //subset(i,s)=subset(i-1,s-v[i]) //subset(i,s)=subset(i-1,s); 条件: //1.i=0,return v[i]==s //2,s=0 return true //v[i]>s--->subset(i-1,s); /*bool subset1(vector<int>& vi, int i,int s) { int A, B; if (i == 0) return vi[0] == s; if (s == 0) return true; if (vi[i] > s) return subset(vi, i - 1, s); A = subset(vi, i - 1, s - vi[i]); B = subset(vi, i - 1, s); return A || B; }*/ bool subset(vector<int>& vi, int s) { vector<vector<bool>> vvi(vi.size(),vector<bool>(s+1)); int A, B; for (int i = 0; i < s + 1;i++) vvi[0][i] =false; vvi[0][vi[0]] = true; for (int i = 0; i < vi.size();i++) { vvi[i][0] = true; } for (int i = 1; i < vi.size();i++) { for (int j = 1; j < s + 1; j++) { if (vi[i]>j) vvi[i][j] = vvi[i - 1][j]; else { A = vvi[i - 1][j - vi[i]]; B = vvi[i - 1][j]; vvi[i][j] = A || B; } } } return vvi[vi.size() - 1][s]; } int main() { int n,tmp; vector<int> vi; cin >> n; for (int i = 0; i < n;i++) { cin >> tmp; vi.push_back(tmp); } cout<<boolalpha<<subset(vi,9)<<endl; cout << boolalpha << subset(vi, 10) << endl; cout << boolalpha << subset(vi, 12) << endl; cout << boolalpha << subset(vi, 9) << endl; cout << boolalpha << subset(vi, 13) << endl; system("pause"); return 0; }




