机器学习数学基础-3-泰勒公式

泰勒公式与拉格朗日

使用泰勒公式的出发点

• 用简单熟悉的多项式来近似替代复杂的函数
• 易计算函数值，导数与积分仍是多项式
• 多项式由它的系数完全确定，其系数又由它在一点的函数值及其导数所确定

---

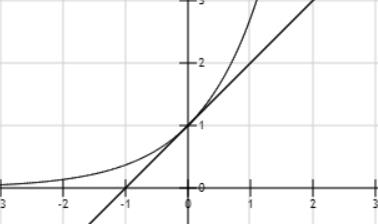
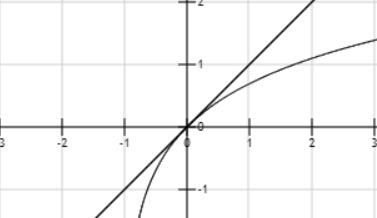
以直代曲

当 \(\lvert x\rvert\) 很小时，\(e^x\approx 1+x\)，\(\ln(1+x)\approx x\)

---

泰勒多项式

\[P_n(x)=f(x_0)+f^{'}(x_0)(x-x_0)+\frac{f^{''}(x_0)}{2！}(x-x_0)^2+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \]

称为 \(f(x)\) 在 \(x_0\) 关于 \((x-x_0)\) 的 \(n\) 阶泰勒多项式

---

麦克劳林公式

在泰勒多项式中，令 \(x=0\) 得：

\[f(x)=f(0)+f^{'}(0)x+\frac{f^{''}(0)}{2!}x^2+\cdots+\frac{f^{(n)}(0)}{n!}x^n+\frac{f^{(n+1)}(\theta x)}{(n+1)!}x^{n+1} \]

其中 \(0<\theta<1\)，称为麦克劳林公式

近似可得：

\[f(x)=f(0)+f^{'}(0)x+\frac{f^{''}(0)}{2!}x^2+\cdots+\frac{f^{(n)}(0)}{n!}x^n \]

---

拉格朗日乘子法

求解：函数 \(z=f(x,y)\) 在条件 \(\varphi(x,y)=0\) 条件下的极值

构造函数 \(F(x,y)=f(x,y)+\lambda\varphi(x,y)\)，其中 \(\lambda\) 称为拉格朗日乘数，求解方程：

\[\begin{cases} F_x(x,y)=f_x(x,y)+\lambda\varphi_x(x,y)=0 \\ F_y(x,y)=f_y(x,y)+\lambda\varphi_y(x,y)=0 \\ \varphi(x,y)=0 \end{cases} \]

求得到 \((x_0, y_0)\) 就是极值点坐标

当有多个变量或是多个约束条件下也可以使用拉格朗日乘子法求解