运用对偶的(对应原始)感知机算法实现线性分类。
参考书目:《统计学习方法》(李航)
算法原理:



代码实现:
环境:win7 32bit + Anaconda3 +spyder
和原始算法的实现基本框架是类似的,只是判断和权值的更新算法有点变化。
1 # -*- coding: utf-8 -*- 2 """ 3 Created on Fri Nov 18 01:29:35 2016 4 5 @author: Administrator 6 """ 7 8 import numpy as np 9 from matplotlib import pyplot as plt 10 11 12 # train matrix 13 def get_train_data(): 14 M1 = np.random.random((100,2)) 15 # 将label加到最后,方便后面操作 16 M11 = np.column_stack((M1,np.ones(100))) 17 18 M2 = np.random.random((100,2)) - 0.7 19 M22 = np.column_stack((M2,np.ones(100)*(-1))) 20 # 合并两类,并将位置索引加到最后 21 MA = np.vstack((M11,M22)) 22 MA = np.column_stack((MA,range(0,200))) 23 24 # 作图操作 25 plt.plot(M1[:,0],M1[:,1], 'ro') 26 plt.plot(M2[:,0],M2[:,1], 'go') 27 # 为了美观,根据数据点限制之后分类线的范围 28 min_x = np.min(M2) 29 max_x = np.max(M1) 30 # 分隔x,方便作图 31 x = np.linspace(min_x, max_x, 100) 32 # 此处返回 x 是为了之后作图方便 33 return MA,x 34 35 # GRAM计算 36 def get_gram(MA): 37 GRAM = np.empty(shape=(200,200)) 38 for i in range(len(MA)): 39 for j in range(len(MA)): 40 GRAM[i,j] = np.dot(MA[i,][:2], MA[j,][:2]) 41 return GRAM 42 43 # 方便在train函数中识别误分类点 44 def func(alpha,b,xi,yi,yN,index,GRAM): 45 pa1 = alpha*yN 46 pa2 = GRAM[:,index] 47 num = yi*(np.dot(pa1,pa2)+b) 48 return num 49 50 # 训练training data 51 def train(MA, alpha, b, GRAM, yN): 52 # M 存储每次处理后依旧处于误分类的原始数据 53 M = [] 54 for sample in MA: 55 xi = sample[0:2] 56 yi = sample[-2] 57 index = int(sample[-1]) 58 # 如果为误分类,改变alpha,b 59 # n 为学习率 60 if func(alpha,b,xi,yi,yN,index,GRAM) <= 0: 61 alpha[index] += n 62 b += n*yi 63 M.append(sample) 64 if len(M) > 0: 65 # print('迭代...') 66 train(M, alpha, b, GRAM, yN) 67 return alpha,b 68 69 # 作出分类线的图 70 def plot_classify(w,b,x, rate0): 71 y = (w[0]*x+b)/((-1)*w[1]) 72 plt.plot(x,y) 73 plt.title('Accuracy = '+str(rate0)) 74 75 # 随机生成testing data 并作图 76 def get_test_data(): 77 M = np.random.random((50,2)) 78 plt.plot(M[:,0],M[:,1],'*y') 79 return M 80 # 对传入的testing data 的单个样本进行分类 81 def classify(w,b,test_i): 82 if np.sign(np.dot(w,test_i)+b) == 1: 83 return 1 84 else: 85 return 0 86 87 # 测试数据,返回正确率 88 def test(w,b,test_data): 89 right_count = 0 90 for test_i in test_data: 91 classx = classify(w,b,test_i) 92 if classx == 1: 93 right_count += 1 94 rate = right_count/len(test_data) 95 return rate 96 97 98 if __name__=="__main__": 99 MA,x= get_train_data() 100 test_data = get_test_data() 101 GRAM = get_gram(MA) 102 yN = MA[:,2] 103 xN = MA[:,0:2] 104 # 定义初始值 105 alpha = [0]*200 106 b = 0 107 n = 1 108 # 初始化最优的正确率 109 rate0 = 0 110 111 112 # print(alpha,b) 113 # 循环不同的学习率n,寻求最优的学习率,即最终的rate0 114 # w0,b0为对应的最优参数 115 for i in np.linspace(0.01,1,100): 116 n = i 117 alpha,b = train(MA, alpha, b, GRAM, yN) 118 alphap = np.column_stack((alpha*yN,alpha*yN)) 119 w = sum(alphap*xN) 120 rate = test(w,b,test_data) 121 # print(w,b) 122 rate = test(w,b,test_data) 123 if rate > rate0: 124 rate0 = rate 125 w0 = w 126 b0 = b 127 print('Until now, the best result of the accuracy on test data is '+str(rate)) 128 print('with w='+str(w0)+' b='+str(b0)) 129 print('---------------------------------------------') 130 # 在选定最优的学习率后,作图 131 plot_classify(w0,b0,x,rate0) 132 plt.show()
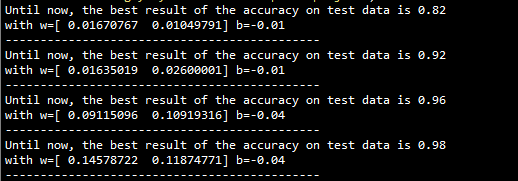
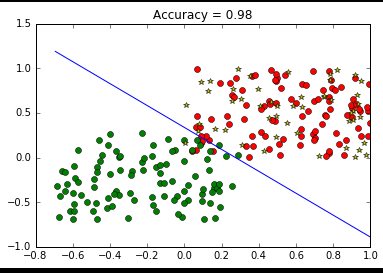
输出: