承接这个PCA的练习,还有一个关于LDA的几何表示。
题目如下:

代码实现LDA如下:LDA.m
clear
clc
% 生成training sample
MU1 = [6 10]';
MU2 = [6 20]';
SIGMA1 = [2 4; 4 9];
SIGMA2 = [2 4; 4 9];
M1 = mvnrnd(MU1,SIGMA1,1000);
M2 = mvnrnd(MU2,SIGMA2,1000);
M = [M1;M2];
m0 = mean(M);
m1 = mean(M1);
m2 = mean(M2);
%between-class scatter matrix-->SB
SB = (length(M1)/length(M)).*(m1-m0)'*(m1-m0)+(length(M2)/length(M)).*(m2-m0)'*(m2-m0);
%within-class scatter matrix -->SW
WM = [0 0; 0 0];
m = [m1;m2];
for(i=1:2)
for (j=(i-1)*1000+1:i*1000)
WM = WM + (M(j,:)-m(i,:))'* (M(j,:)-m(i,:));
end
end
SW = (WM)/length(M);
%求最大特征值及其对应的特征向量
[V,D] = eig(inv(SW)*SB);
u = V(:,2);
v = u*(1/sqrt(u'*SW*u));
for (i=1:2000)
VD(i,:) = dot(v,M(i,:))*v';
end
%画在同一坐标系下
plot(VD(:,1),VD(:,2),'.',M1,M2,'.')
输出如下:
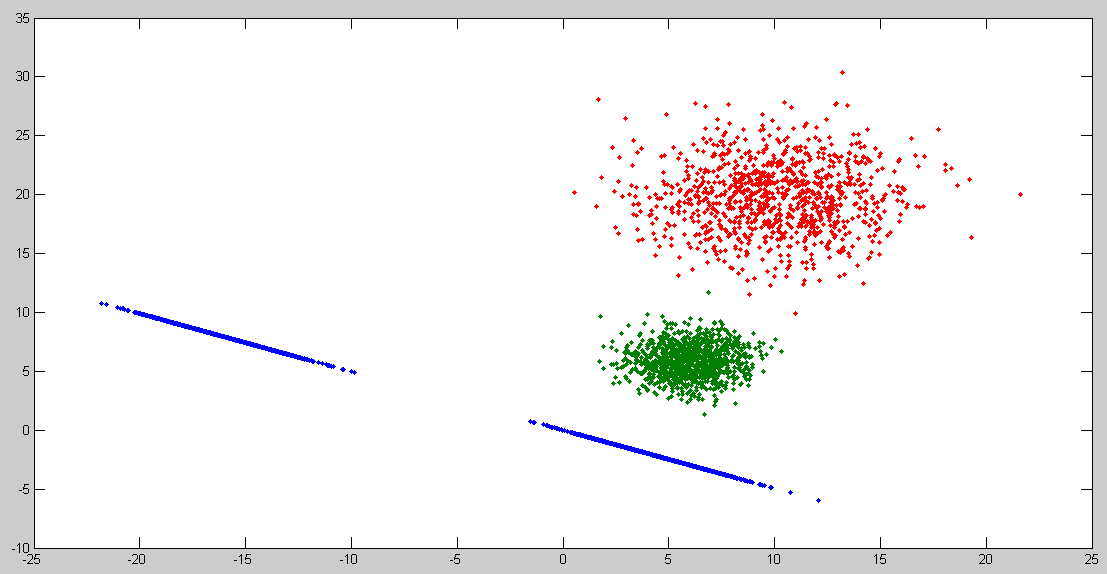
可以和上一次的PCA比较一下。
执行如下命令(之前已经写了PCA.m和LDA.m):

输出:



