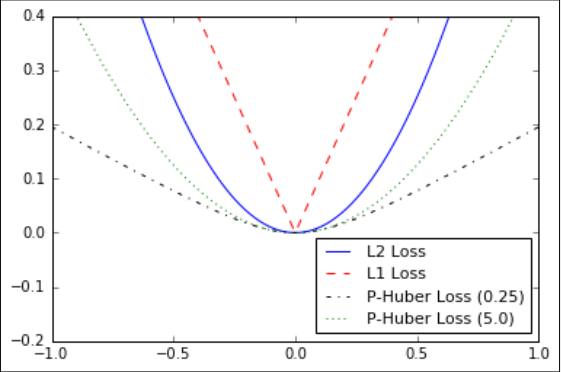
1. L2范数损失函数,也叫欧几里得损失函数,实际上是预测值到目标的距离的平方,tensorflow中用法:tf.nn.l2_loss(),这个损失函数的优点在于曲线在接近目标时足够平缓,所以可以利用这个特点在接近目标时,逐渐缓慢收敛过去。这个损失函数一般用在回归问题。
2. L1范数损失函数,采用绝对值,特点是对异常值曲线不像L2范数损失函数那样陡峭,由于曲线在目标出不平滑,所以可能导致算法在这个点收敛不是很好。
3. Pseudo-Huber损失函数,是一个连续且平滑的对Huber损失函数的近似。这个函数在目标附近是凸(convex)的,并且对数据中的游离点较不敏感,具有上述的两个损失函数的优点。需要一个额外的参数delta决定曲线的斜率。
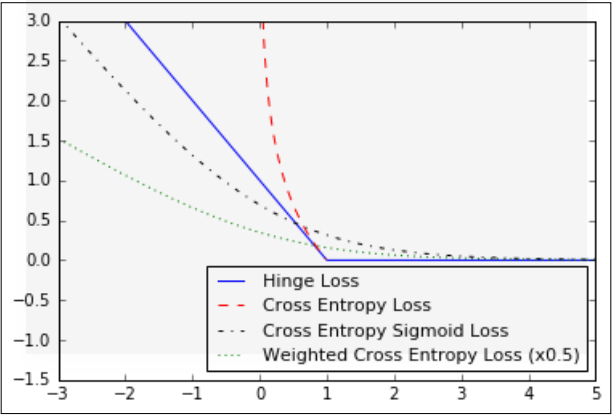
4. Hinge loss损失函数,在支持向量机里面最常用,但是也可以被用在神经网络中,它计算到两个目标分类1, -1的损失。
5. 交叉熵损失函数,表示的是两个概率分布之间的距离,值越小,两个概率分布之间的距离值越近。交叉熵克服方差代价函数更新权重过慢的问题。--对这个不是很理解。
假设一个三分类问题,正确答案是(1,0,0),有两个答案,(0.5,0.4,0.1)和(0.8,0.1,0.1)那么两个答案和正确答案的交叉熵分别是:
答案(0.5,0.4,0.1):-(1*lg0.5+0*lg0.4+0*lg0.1) = 0.3
答案(0.8,0.1,0.1):-(1*lg0.8 + 0*lg0.1 + 0*lg0.1) = 0.1
可以看到越接近的概率分布具有越小的交叉熵值。
summary:




