有关容斥原理的一些东西
有关容斥原理的一些东西
容斥原理的形式化证明:
设有若干个物品以及\(k\)种属性,每个物品都有若干种属性。
设有函数\(f(S)\)表示至少拥有属性集合\(S\)的物品个数
参考一个很简单的\(k=3\)的情况
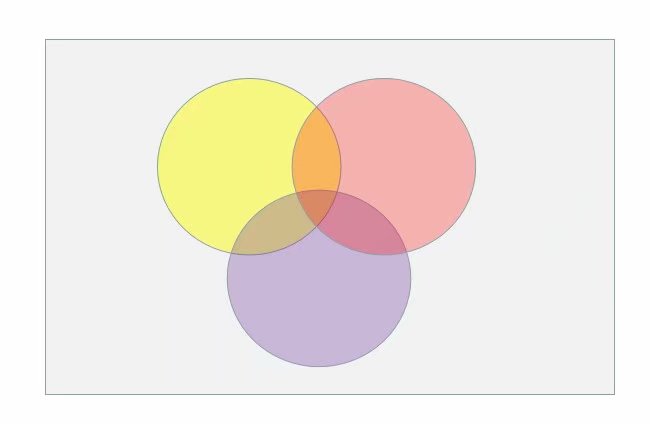
每种颜色的圆的物品集合都拥有同一个属性,圆外面是没有属性的物品,设全集\(U\)为所有属性的集合。
一般来说,我们要求三个圆面积的交。
形式化的说,我们要求至少拥有一种属性的物品的集合大小,也就是有属性的物品有多少个。
公式说,这个集合大小为
说白了在\(k=3\)就是一个圆公共-两个圆公共+三个圆公共,大家都知道。
考虑一个正经的证明。
大体思路:证明每个有属性的物品的计算次数是\(1\)
设有一个\(p\)种属性的物品,考虑哪一些集合会出现\(Ta\)
每种大小不大于\(p\)的集合都可能对\(Ta\)有贡献,即为
通过组合数学 \(\binom{n}{m} = \binom{n-1}{m} + \binom{n-1}{m-1}\)的这个公式,我们化简一下上面的式子,就等于\(1\)啦。
多重集组合数
设有多重集\(\{x_1\cdot c_1,x_2\cdot c_2,\dots,x_k\cdot c_k\}\),\(x\)是元素的值,而\(c\)是这个值的个数,设\(C=\sum\limits_{i=1}^k c_i\)。
先考虑多重集的排列数,显然为
假设现在要取\(n\)个元素。
首先我们不考虑每种元素的上限时(也就是当每种元素都有无限个的时候)的方案数
从组合的意义出发,相当于把\(n\)个元素有序的划分成\(k\)组,每组可以为空的方案数。
等价于\(n\)个\(0\),\(k-1\)个\(1\)的排列数,由多重集的排列数,为
然后我们考虑至少有一种元素取多了的方案数
考虑\(x_i\)取了至少\(c_i+1\)个的方案数,首先我们把这\(c_i+1\)个取出来,然后再随便取,为\(\binom{n+k-c_i-2}{k-1}\)
则至少某一种元素取多了的方案数为
类比可以得到至少两种元素取多了的方案数等等
如果把多取了某个元素当做一个属性,每一种取法当做物品,那么就可以套用上面的容斥原理了。
即为
上式代表的是至少某一种元素取多了的方案数,形象化的说,代表那三个圆的面积交。
则总方案为无限制的多重集的总排列数(全集)减去至少某一个元素多取了个数的方案数(面积并)
注意我们求解这个的复杂度是至少要枚举\(2^k\)种分配情况的,所以\(k=20\)左右时再想一想是不是这个做法。事实上还可以\(f_{i,j}\)代表前\(i\)种集合选了\(j\)个元素进行\(DP\)做。
一个小问题
一个\(a \times b\)的矩形,每个位置的值在整数\([0,s]\)中,要求每行每列的最大值均为\(s\),计算有多少取值的方案。
-
为什么要专门提出这个问题?
-
从个人角度来看,先有了这个题(这其实是某个题的子问题)的我对容斥的思考,为了想明白容斥过程,才有了上面的东西。
Solution:
设\(f_i\)为至少有\(i\)行的限制不满足条件时的方案(需要保证每一列都满足条件)
\(f_i=\binom{a}{i} \times(s^i \times ((s+1)^{a-i}-s^{a-i}))^b\)
方案数就是\(\sum\limits_{i=0}^a (-1)^i \times f_i\)。
先解释\(f_i\),如下图,蓝色的部分为满足的行,黄色的为不满足的行。
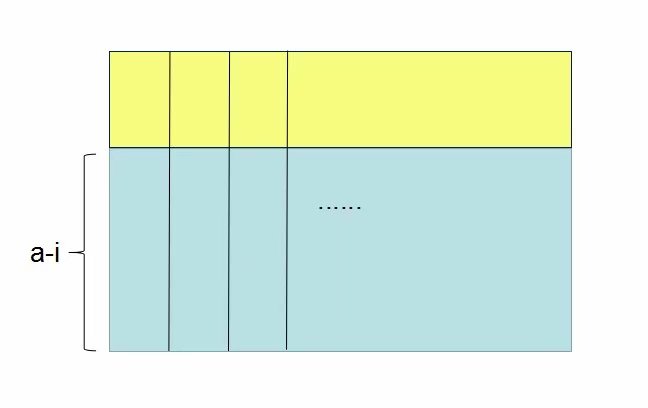
我们一列一列的填,把保证列满足的条件放在蓝色的地方。
于是蓝色的地方有总填法方案数\((s+1)^{a-i}\)减去每一行都不填最大值的方案数\(s^{a-i}\)得到至少有一个位置填了\(s\)的方案数。
然后黄色的地方每个位置只能填\([0,s-1]\),于是是\(s^i\)种填法了。
对每一列都这么填,于是是\(b\)次方,然后枚举哪\(i\)行不满足,就是\(f_i\)了。
然后是后面的容斥,不知道你有没有发现,上面两个地方出现了至少都是加黑的,还有一处是斜体,这是为了警示和区分,反正我想了好久才明白。
有没有觉得 \(\text{至少0个不满足的方案-至少1个不满足的方案=所有条件都满足的方案}\)
事实上这样说没问题,但是这个“至少”和\(f_i\)中的“至少”的意义并不一样。
可以像求多重集的组合数一样把意义套到容斥里面,然后结合上面的斜体和黑体的为什么不一样理解一下,就可以明白区别在哪里了。
长期更新...


