洛谷 P3302 [SDOI2013]森林 解题报告
P3302 [SDOI2013]森林
题目描述
小\(Z\)有一片森林,含有\(N\)个节点,每个节点上都有一个非负整数作为权值。初始的时候,森林中有\(M\)条边。
小Z希望执行\(T\)个操作,操作有两类:
Q x y k查询点\(x\)到点\(y\)路径上所有的权值中,第\(k\)小的权值是多少。此操作保证点\(x\)和点\(y\)连通,同时这两个节点的路径上至少有\(k\)个点。
L x y在点\(x\)和点\(y\)之间连接一条边。保证完成此操作后,仍然是一片森林。
为了体现程序的在线性,我们把输入数据进行了加密。设\(lastans\)为程序上一次输出的结果,初始的时候\(lastans\)为\(0\)。
对于一个输入的操作Q x y k,其真实操作为Q x^lastans y^lastans k^lastans。
对于一个输入的操作L x y,其真实操作为L x^lastans y^lastans。其中^运算符表示异或,等价于pascal中的xor运算符。
请写一个程序來帮助小Z完成这些操作。
对于所有的数据,\(n,m,T<=8*10^4\)
.
输入输出格式
输入格式:
第一行包含一个正整数\(testcase\),表示当前测试数据的测试点编号。保证\(1<=testcase<=20\)。
第二行包含三个整数\(N\),\(M\),\(T\),分别表示节点数、初始边数、操作数。
第三行包含\(N\)个非负整数表示 \(N\)个节点上的权值。
接下来 \(M\)行,每行包含两个整数\(x\)和\(y\),表示初始的时候,点\(x\)和点\(y\)之间有一条无向边。
接下来 \(T\)行,每行描述一个操作,格式为”Q x y k“或者”L x y “,其含义见题目描述部分。
输出格式:
对于每一个第一类操作,输出一个非负整数表示答案。
说明:
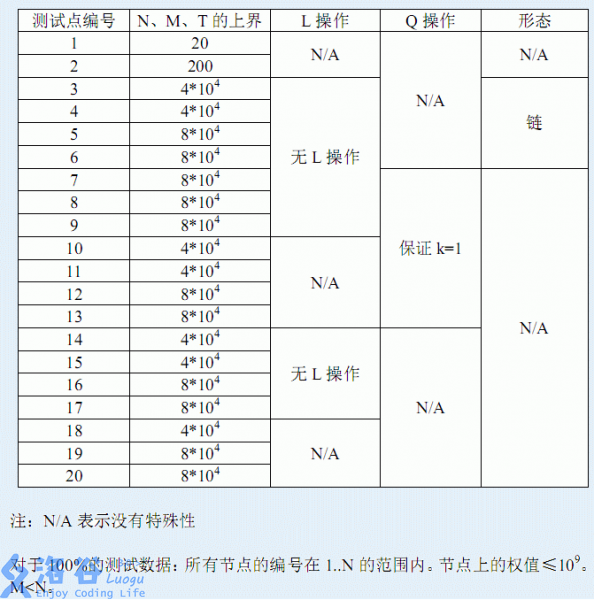
先吐槽:第一行原来给的是测试点编号我以为是数据组数还T了一会儿
动态维护树上两点间第\(k\)值
LCT不能直接维护第\(k\)值,也很难嵌套其他数据结构,所以我们不考虑她
发现只有加边没有删边,考虑使用主席树启发式合并
具体来说
加边时
把节点少的主席树合并到节点多的主席树上面,复杂度\(slogs\),\(s\)为小主席树的大小,同时动态更新父节点的倍增数组,复杂度也是\(slogs\)的
查询时
进入两个点以及它们的lca和lca的爹的主席树中上上下下加加减减
总复杂度:\(O(nlog^2n)\)
Code:
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ls ch[now][0]
#define rs ch[now][1]
#define ols ch[las][0]
#define ors ch[las][1]
const int N=3e5+10;
int ch[N*30][2],sum[N*30],tot;
int f[N][20],dep[N],n,m,n_,t,tmp,siz[N],root[N],a[N],b[N],testcase;
void updata(int now){sum[now]=sum[ls]+sum[rs];}
int rebuild(int las,int l,int r,int pos)
{
int now=++tot;
if(l==r) {sum[now]+=sum[las]+1;return now;}
int mid=l+r>>1;
if(pos<=mid)
{
ls=rebuild(ols,l,mid,pos);
rs=ors;
}
else
{
ls=ols;
rs=rebuild(ors,mid+1,r,pos);
}
updata(now);
return now;
}
int head[N],to[N<<1],Next[N<<1],cnt;
void add(int u,int v)
{
to[++cnt]=v,Next[cnt]=head[u],head[u]=cnt;
}
int dfs(int now,int fa)
{
int s=1;
root[now]=rebuild(root[fa],1,n,b[now]);
f[now][0]=fa;
dep[now]=dep[fa]+1;
for(int i=1;i<=18;i++)
f[now][i]=f[f[now][i-1]][i-1];
for(int i=head[now];i;i=Next[i])
if(to[i]!=fa)
s+=dfs(to[i],now);
return s;
}
void swap(int &x,int &y){tmp=x,x=y,y=tmp;}
int rt(int now)
{
for(int i=18;~i;i--)
if(f[now][i])
now=f[now][i];
return now;
}
void Merge(int x,int y)
{
int rx=rt(x),ry=rt(y);
if(siz[rx]<siz[ry]) swap(rx,ry),swap(x,y);
add(x,y),add(y,x);
siz[rx]+=dfs(y,x);
}
int LCA(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=18;~i;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y) return x;
for(int i=18;~i;i--)
if(f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
int query(int rt1,int rt2,int rt3,int rt4,int l,int r,int k)
{
if(l==r) return a[l];
int mid=l+r>>1,s=sum[ch[rt1][0]]+sum[ch[rt2][0]]-sum[ch[rt3][0]]-sum[ch[rt4][0]];
if(s>=k) return query(ch[rt1][0],ch[rt2][0],ch[rt3][0],ch[rt4][0],l,mid,k);
else return query(ch[rt1][1],ch[rt2][1],ch[rt3][1],ch[rt4][1],mid+1,r,k-s);
}
int main()
{
freopen("data.in","r",stdin);
freopen("data.out","w",stdout);
scanf("%d",&testcase);
tot=0,cnt=0;
scanf("%d%d%d",&n_,&m,&t);
for(int i=1;i<=n_;i++) scanf("%d",a+i),b[i]=a[i];
std::sort(a+1,a+1+n_);
n=std::unique(a+1,a+1+n_)-a-1;
for(int i=1;i<=n_;i++) b[i]=std::lower_bound(a+1,a+1+n,b[i])-a;
for(int u,v,i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add(u,v),add(v,u);
}
for(int i=1;i<=n_;i++)
if(!f[i][0])
siz[i]=dfs(i,0);
int lastans=0;char op[4];
for(int u,v,k,i=1;i<=t;i++)
{
scanf("%s%d%d",op,&u,&v);
u^=lastans,v^=lastans;
if(op[0]=='Q')
{
scanf("%d",&k);
k^=lastans;int lca=LCA(u,v);
printf("%d\n",lastans=query(root[u],root[v],root[lca],root[f[lca][0]],1,n,k));
}
else
Merge(u,v);
}
return 0;
}
2018.9.4

