BZOJ [Ctsc2002] Award 颁奖典礼 解题报告

[Ctsc2002] Award 颁奖典礼

Description

IOI2002的颁奖典礼将在YONG-IN Hall隆重举行。人们在经历了充满梦幻的世界杯之后变得更加富于情趣。为了使颁奖典礼更具魅力，有人建议在YONG-IN Hall中搭建一个I字型的颁奖台，以此代表信息学Informatics。考虑到比赛的赞助商们可能要在YONG-IN Hall中摆设了许多展示台，他们可能不愿意移动展示台的位置。你作为IOI2002的金牌得主自然地成为了他们求助的对象。 YONG-IN Hall是一个矩形的网格区域。每个赞助商的展示台都占据了若干个单位网格。I型颁奖台将正向搭建，且平行于YONG-IN Hall的边缘。I型颁奖台是由三个矩形相接叠成的，其中上方和下方的矩形的两侧必须都超出中间的矩形，否则将被误解成T, L, J等字母。

例如：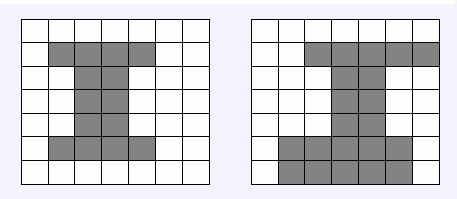

这是两个合法的I型颁奖台，而以下三种情况均不合法：

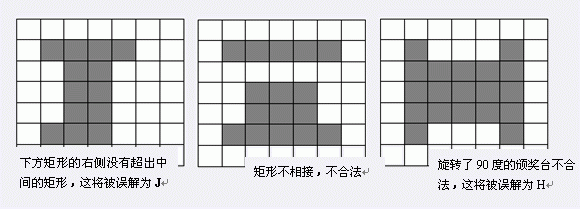
希望你编程寻找面积最大的I型颁奖台，使其不覆盖任何展示台。

Input

第一行包含两个正整数n, m(1<=n,m<=200)，分别表示YONG-IN Hall的矩形网格区域的行数和列数。以下n行每行包含m个数字，非0即1，每个数字描述一个单位网格，1表示该单位网格存在展示台，0表示该单位网格不存在展示台。

Output

仅包含一个正整数，表示最大的I型颁奖台的面积。如果不存在合法的I型颁奖台，则输出0。

---

大力DP+前缀和优化

把字母"I"看成三个矩形
\(dp[i][k][l][r]\)表示第\(i\)行做到第\(k\)个矩形左边界为\(l\)右边界为\(r\)的最大面积

枚举四维后我们发现不换矩形可以\(O(1)\)转移

但换矩形得多枚举两维，于是用RMQ前缀和先处理一下作为优化

---

Code：
DewOS：我怀疑我自己程序写的有问题但它过了就不管啦

#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
const int N=202;
int dp[3][N][N][N],f[2][N][N],f0[N][N];
int n,m,is[N][N],ans;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&is[i][j]);
            f0[i][j]=f0[i][j-1]+is[i][j];
        }
    memset(dp,-0x3f,sizeof(dp));
    memset(f,-0x3f,sizeof(f));
    memset(dp[0][0],0,sizeof(dp[0][0]));
    for(int i=1;i<=n;i++)
        for(int k=2;k>=0;k--)
        {
            for(int l=1;l<=m;l++)
                for(int r=l;r<=m;r++)
                {
                    if(f0[i][r]==f0[i][l-1])
                    {
                        if(!k) dp[k][i-1][l][r]=max(dp[k][i-1][l][r],0);
                        dp[k][i][l][r]=dp[k][i-1][l][r]+(r+1-l);
                        if(k==1) dp[k][i][l][r]=max(dp[k][i][l][r],f[k-1][l-1][r+1]+(r+1-l));
                        else if(k==2) dp[k][i][l][r]=max(dp[k][i][l][r],f[k-1][l+1][r-1]+(r+1-l));
                    }

                }
            if(!k)
            {
                for(int l=1;l<=m;l++)
                    for(int r=m;r>=l;r--)
                        f[k][l][r]=max(dp[k][i][l][r],max(f[k][l][r+1],f[k][l-1][r]));
            }
            else if(k==1)
            {
                for(int l=m;l;l--)
                    for(int r=l;r<=m;r++)
                        f[k][l][r]=max(dp[k][i][l][r],max(f[k][l][r-1],f[k][l+1][r]));
            }
            else
            {
                for(int l=1;l<=m;l++)
                    for(int r=l;r<=m;r++)
                        ans=max(ans,dp[k][i][l][r]);
            }
        }
    printf("%d\n",ans);
    return 0;
}

---

2018.7.26