CF825F String Compression 解题报告
CF825F String Compression
题意
给定一个串s,其中重复出现的子串可以压缩成 “数字+重复的子串” 的形式,数字算长度。
只重复一次的串也要压。
求压缩后的最小长度。
数据范围
\(0 \le |s| \le 8,000\)
时空范围:
2sec 512mb
时空范围让我们基本可以\(O(N^2)\)做了
先考虑如果原串的每一个子串都求出了它的压缩后长度存在了\(cnt[i][j]\)里,我们就可以很方便的做DP了
令\(dp[i]\)表示长为\(i\)的串的最小压缩程度
\(dp[i]=min_{j=0}^{i-1}(dp[j]+cnt[j+1][i])\)
考虑求出每一个串的压缩后长度
枚举每一个位置为起点的子串,求出此时的\(nxt\)数组
则如果子串的子串中有从头开始循环的串,我们可以用子串的子串的长度\(len-nxt[len]\)得到循环节的长度
如下图
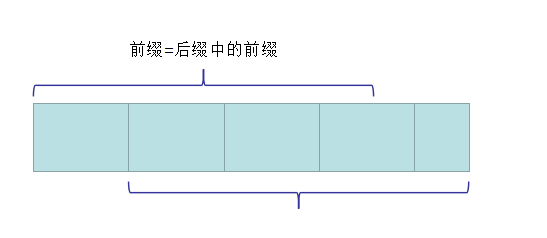
如果长度可以整除循环节的长度,则求出长度。否则直接为原长度+1
Code:
#include <cstdio>
#include <cstring>
int min(int x,int y){return x<y?x:y;}
const int N=8010;
int dp[N],nxt[N],cnt[N][N],n;
char c[N];
int get(int x)
{
int cnt=0;
while(x)
{
cnt++;
x/=10;
}
return cnt;
}
int main()
{
scanf("%s",c+1);
n=strlen(c+1);
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=n;i++)
{
memset(nxt,0,sizeof(nxt));
cnt[i][i]=2;
nxt[i]=i-1;
for(int j=i+1,k=i-1;j<=n;j++)
{
while(k!=i-1&&c[k+1]!=c[j]) k=nxt[k];
if(c[k+1]==c[j]) k++;
nxt[j]=k;
int len=j+1-i;
if(len%(len-nxt[j]+i-1)==0)
cnt[i][j]=(len-nxt[j]+i-1)+get(len/(len-nxt[j]+i-1));
else
cnt[i][j]=len+1;
}
}
for(int i=1;i<=n;i++)
for(int j=0;j<i;j++)
dp[i]=min(dp[i],dp[j]+cnt[j+1][i]);
printf("%d\n",dp[n]);
return 0;
}
2018.7.25


 浙公网安备 33010602011771号
浙公网安备 33010602011771号