斜率优化学习笔记
斜率优化学习笔记
概论:对形如\(dp[i]=min(dp[j]+c[i]*c[j])\)类型的转移方程的优化,其中有关于\((i,j)\)的乘积项的式子。
例题:洛谷P2365 任务安排
题目描述
\(N\)个任务排成一个序列在一台机器上等待完成(顺序不得改变),这\(N\)个任务被分成若干批,每批包含相邻的若干任务。从时刻0开始,这些任务被分批加工,第\(i\)个任务单独完成所需的时间是\(T_i\)。在每批任务开始前,机器需要启动时间\(S\),而完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。每个任务的费用是它的完成时刻乘以一个费用系数\(F_i\)。请确定一个分组方案,使得总费用最小。
例如:\(S=1\);\(T=\{1,3,4,2,1\}\);\(F=\{3,2,3,3,4\}\)。如果分组方案是\(\{1,2\}\)、\(\{3\}\)、\(\{4,5\}\),则完成时间分别为\(\{5,5,10,14,14\}\),费用\(C=\{15,10,30,42,56\}\),总费用就是153。
输入输出格式
输入格式:
第一行是\(N(1<=N<=5000)\)。
第二行是\(S(0<=S<=50)\)。
下面N行每行有一对数,分别为\(T_i\)和\(F_i\),均为不大于100的正整数,表示第\(i\)个任务单独完成所需的时间是\(T_i\)及其费用系数\(F_i\)。
输出格式:
一个数,最小的总费用。
先考虑\(O(N^2)\)的做法
因为分的批数是不定的,所有我们为了避免算后面的时候要用到前面分了多少批这个状态,我们采用费用提前的思想,在处理前面时把\(S\)产生的费用给计算了。
方程:\(f[i]\)代表前\(i\)个任务分成若干批产生的最小费用
转移:\(f[i]=min_{i=0}^{i-1}(f[j]+t[i]*(c[i]-c[j])+S*(c[n]-c[j]))\)
其中,\(t,c\)分别是任务时间和费用的前缀和的数组
考虑将状态转移方程化简:
\(f[j]=(S+t[i])*c[j]+f[i]-t[i]*c[i]-S*c[n]\)
注意:我们这里把\(min\)去掉了,是把\(j\)的取值集合所映射的\(f[j]\)和\(c[j]\)分别作为函数的\(f(x)\)和\(x\)
那么这个一次函数的斜率\(k\)就等于\((S+t[i])\),而截距\(b\)等于\(f[i]-t[i]*c[i]-S*c[n]\)
我们想让这个\(f[i]\)最小,那么其实就等价于\(b\)最小,在坐标系中,如果我们拿一个已知斜率的直线向上滑动,当它第一次碰见取值集合内的点\((c[j],f[j])\)时,就取到了它的最小值
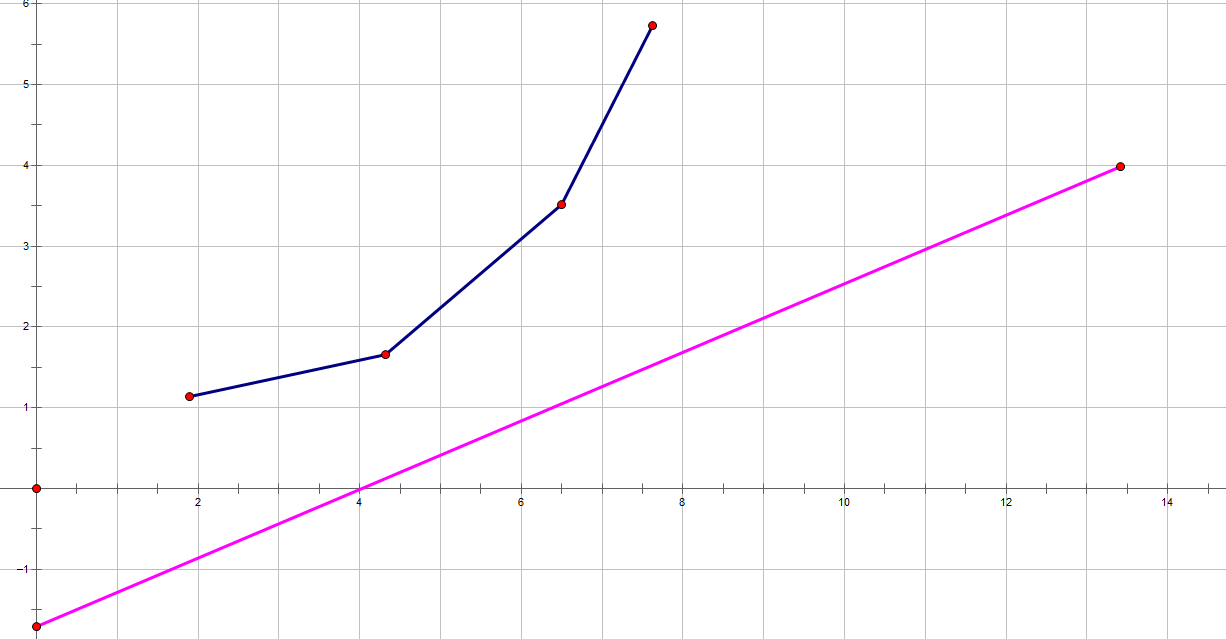
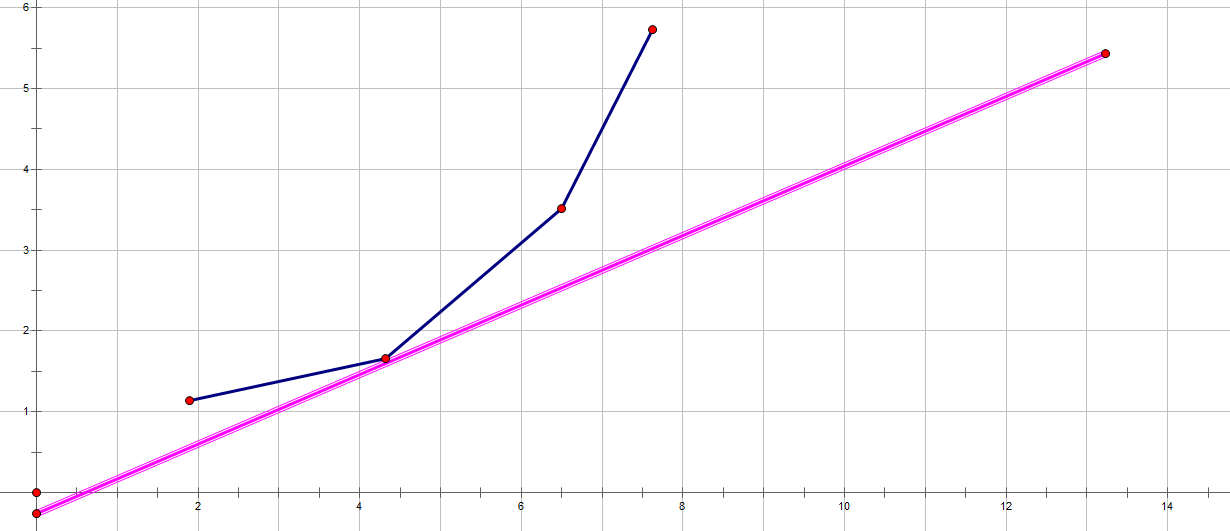
1.考虑什么时候一个点可以取到最小值
通过手玩我们发现(对于这个手玩真的是最好的理解方式了)
对于点\(J_2\),当以\(x\)为关键字排序后的两个相邻的点\(J_1\)和\(J_3\)(在此题中对应\(c[j]\)的单调性)
当斜率\(k_1<k_0<k_2\)时,此点就是最优转移点
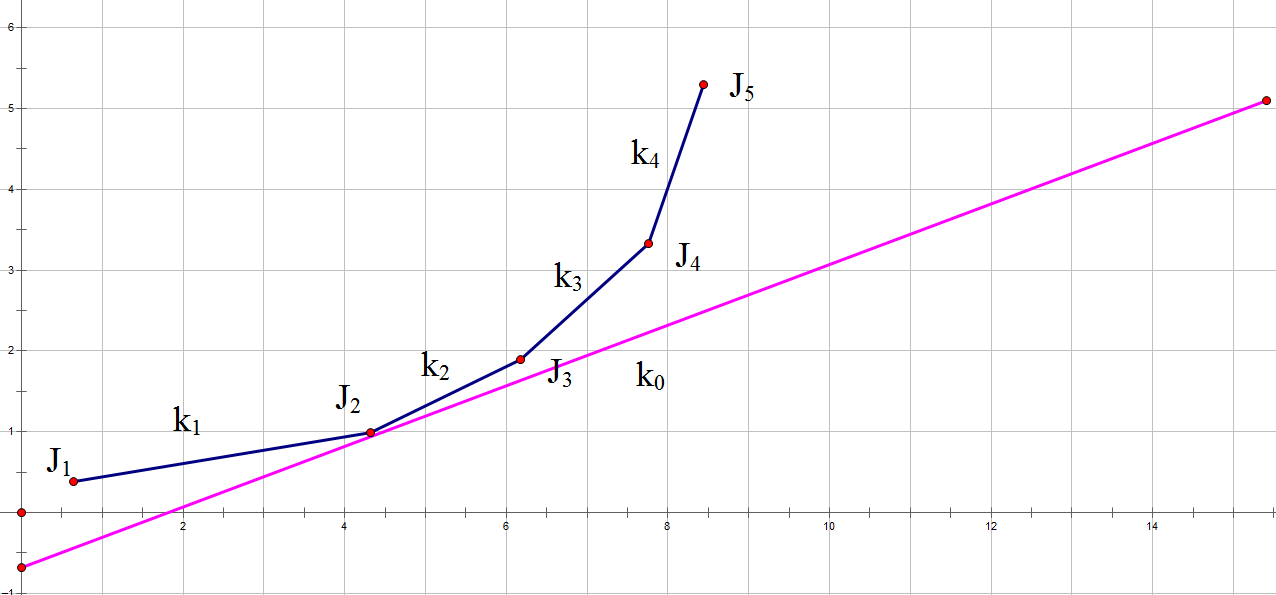
2.考虑什么时候一个点可能可以取到最小值,什么时候一定不能
如下图,当斜率\(k_1<k_2\)时,\(J_2\)是有机会的,此时三个点下凸
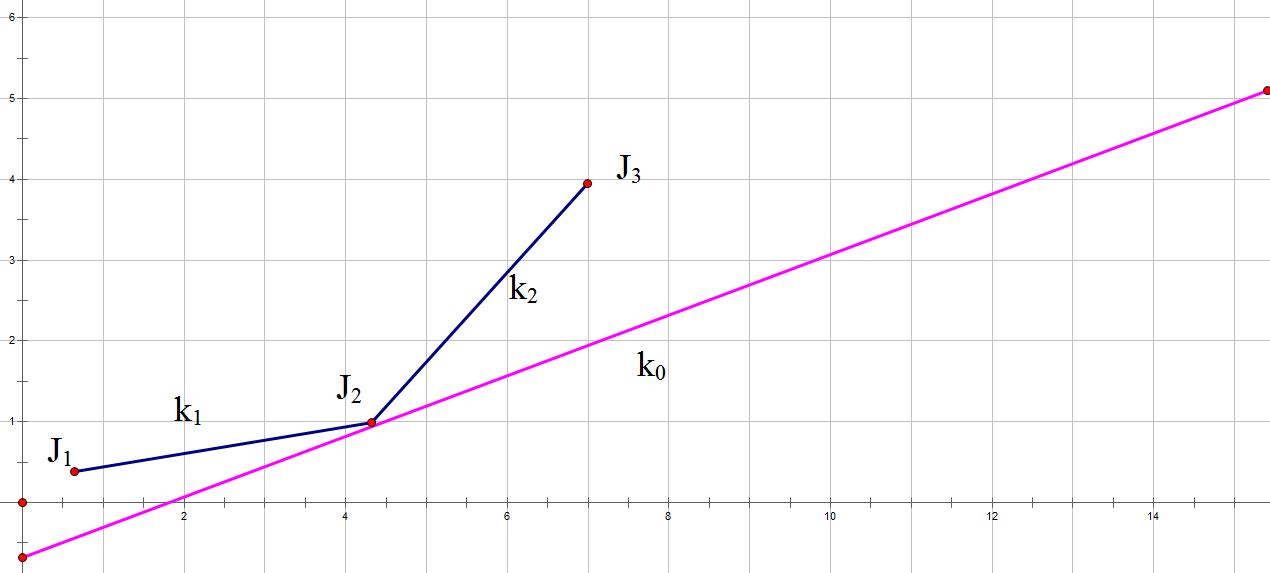
当斜率\(k_1>=k_2\)时,\(J_2\)不会有一点机会,此时三个点上凸
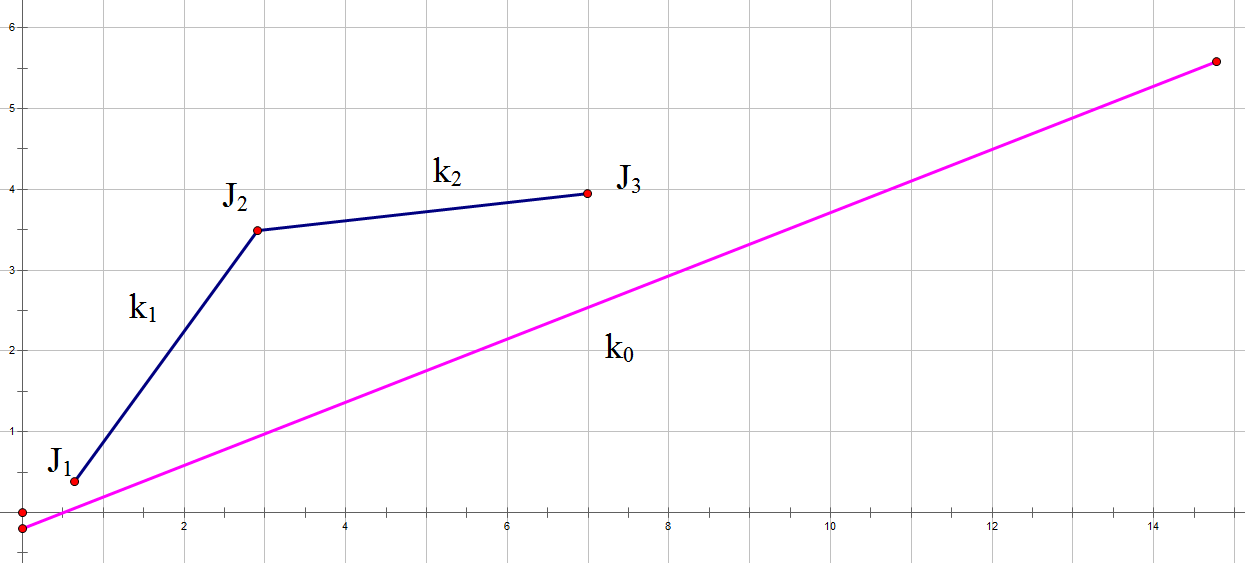
此时我们就可以用单调队列维护一个点集了,其中相邻点的斜率\(k\)必定是递增的
当需要做出决策的时候,我们二分这个点集,找到最优转移点。
针对于此题,我们发现每个决策点的斜率\(S+t[i]\)是单调递增的,那么我们可以直接维护队首,保证每次从队首转移。即当当前斜率大于队首与第二个点之间的斜率时,就出队。
统计完答案后再用二元组\((f[i],c[i])\)更新队尾的元素,然后将它放进去
Code:
#include <cstdio>
#include <cstring>
const int N=5010;
int f[N],t[N],c[N],n,S,q[N],l,r;
int main()
{
scanf("%d%d",&n,&S);
for(int i=1;i<=n;i++)
{
scanf("%d%d",t+i,c+i);
t[i]+=t[i-1];
c[i]+=c[i-1];
}
memset(f,0x3f,sizeof(f));
f[0]=0;
l=1,r=1;//注意此时已经把0作为元素放入了q[1]中去了
for(int i=1;i<=n;i++)
{
while(l<r&&f[q[l+1]]-f[q[l]]<=(S+t[i])*(c[q[l+1]]-c[q[l]])) l++;
f[i]=f[q[l]]+t[i]*c[i]+S*c[n]-c[q[l]]*(S+t[i]);
while(l<r&&(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])<=(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]])) r--;
q[++r]=i;
}
printf("%d\n",f[n]);
return 0;
}
2018.7.16


