洛谷 P1325 雷达安装 解题报告

P1325 雷达安装

题目描述

描述：

假设海岸线是一条无限延伸的直线。它的一侧是陆地，另一侧是海洋。每一座小岛是在海面上的一个点。雷达必须安装在陆地上（包括海岸线），并且每个雷达都有相同的扫描范围d。你的任务是建立尽量少的雷达站，使所有小岛都在扫描范围之内。

数据使用笛卡尔坐标系，定义海岸线为x轴。在x轴上方为海洋，下方为陆地。

输入输出格式

输入格式：

第一行包括2个整数n和d，n是岛屿数目，d是雷达扫描范围。

接下来n行为岛屿坐标。

输出格式：

一个整数表示最少需要的雷达数目，若不可能覆盖所有岛屿，输出“-1”。

输入输出样例

输入样例#1：

3 2
1 2
-3 1
2 1

输出样例#1：

2

样例1如图所示

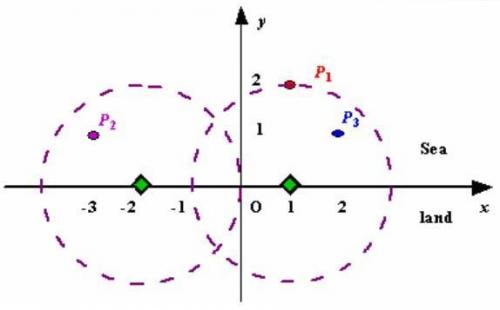
说明

\(n \le 1000,d \le 20000\)

\(|x_i| \le 2 \times 10^6,0 \le y_i \le 20000\)

---

贪心。

因为雷达只能安排在\(x\)轴上，我们可以把问题进行转换。

每一个岛屿在\(x\)轴上都有一条线段（或者是点）可以覆盖它。

于是问题就成了，用最少的点覆盖所有的线段。

把线段按右端点排序，从左往右扫描。对于每一个右端点对应的区间，如果它没有被前一个安排过的点覆盖，那么就为它安排一个点。

解释两个东西：

1. 为什么只检查前一个安排过的点，因为如果前一个安排过的点不能照看它，它也不可能被更左的端点覆盖
2. 是什么保证了它是对的？这样决策，保证了满足当前需求（覆盖所有左边的区间），为后面的需求（右边需要覆盖的区间）产生了最优的状态集合，其他的状态不可能比它还优。是一种决策包容性，这种决策对未来的集合是最大的。

---

Code:

#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstdlib>
const int N=1010;
double d;
struct node
{
    double x,y,r;
    bool friend operator <(node n1,node n2)
    {
        return n1.r<n2.r;
    }
}loc[N];
int n;
void init()
{
    int flag=0;
    scanf("%d%lf",&n,&d);
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf",&loc[i].x,&loc[i].y);
        if(d>=loc[i].y)
            loc[i].r=sqrt(d*d-loc[i].y*loc[i].y)+loc[i].x;
        else
            flag=1;
    }
    if(flag) {printf("-1\n");exit(0);}
    std::sort(loc+1,loc+1+n);
}
double get(double x1,double y1,double x2,double y2)
{
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
void work()
{
    double las=loc[1].r;
    int ans=1;
    for(int i=2;i<=n;i++)
    {
        if(get(loc[i].x,loc[i].y,las,0)>d)
            ans++,las=loc[i].r;
    }
    printf("%d\n",ans);
}
int main()
{
    init();
    work();
    return 0;
}

---

2018.7.12