最大权闭合子图
最大权闭合子图
一、概念
(1) 闭合图
在图\(G\)中,若子图\(G'=(V,E)\)满足其中所有点的出边所指向的点仍属于集合\(G'\),则成这个子图为闭合图。
(2) 最大权闭合子图
给集合\(G\)中每个点赋予点权,点权之和最大的闭合子图称为最大权闭合子图。
二、求解
(1) 考虑一个有向图\(G\)
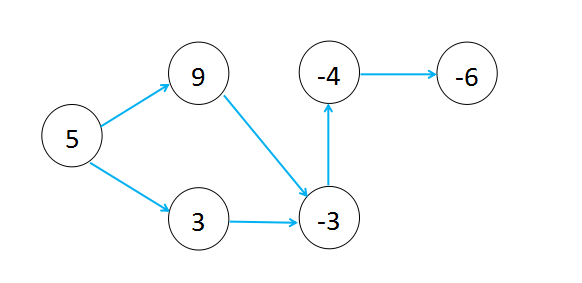
边权这里代表的是依照题意而连接的关系。
(2) 将正点权上发,将负点权下放,分别连接超级源点\(S\)和超级汇点\(T\)
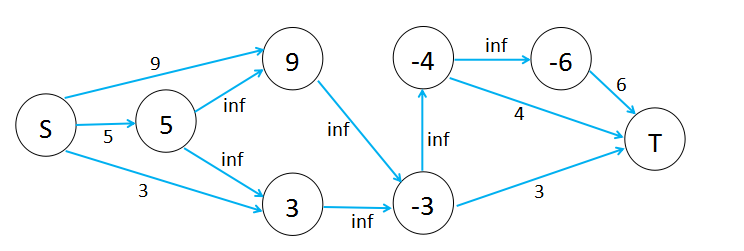
先别急为什么负点权连出正边权和原关系连inf,继续往下看
(3) 找到一个割集
/*- 性质
①这个割集一定是简单割。
简单割:任取$E \in$割集,它一定连接$S$或$T$
证明:权值为inf的点不可能被割掉
②图$S$(即含超级源点$s$的图)一定是一个闭合图,且这个闭合图和简单割一一对应
闭合图根据割的定义其实是一定的
*/
好吧我在上面的定义中有点不太明白
我觉得图的任意割集产生的与源点S相连的图一定是闭合图也是对的=_=。。
(4) 求解最小割
引理:最小割产生的\(S\)图一定是一个最大权闭合图
证明:设\(S\)图的点权之和为\(C=C_1+C_2\),其中正点权为\(C_1\),负点权为\(C_2\)(这个是负的)。设割集中边权和为\(W=W_1+W_2\),正边权(与\(S\)相连的被割掉的边)和为\(W_1\),负边权和为\(W_2\)(这个是正的)
\(C+W=C_1+C_2+W_1+W_2\)
因为负点归为\(S\)得割掉与\(T\)相连的边,所以\(C_2+W_2=0\)
\(C+W=C_1+W_1\)
显然右边即为图\(G\)中所有正点权之和,即为\(Sum\),是一个定值。
\(C=Sum-W\)
若使\(C\)最大,则\(W\)最小,当\(W\)在数值上最小的时候,即为最小割
(5) 实际问题建模(我做一个应该就会更新一个啦)


