洛谷 P1939 【模板】矩阵加速(数列) 解题报告
P1939 【模板】矩阵加速(数列)
题目描述
a[1]=a[2]=a[3]=1
a[x]=a[x-3]+a[x-1] (x>3)
求a数列的第n项对1000000007(10^9+7)取余的值。
输入输出格式
输入格式:
第一行一个整数T,表示询问个数。
以下T行,每行一个正整数n。
输出格式:
每行输出一个非负整数表示答案。
说明
对于30%的数据 n<=100;
对于60%的数据 n<=2*10^7;
对于100%的数据 T<=100,n<=2*10^9;
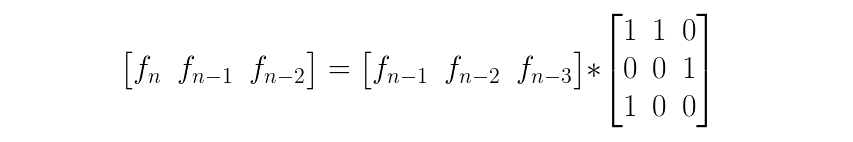
直接套矩阵快速幂即可
Code:
#include <cstdio>
#include <cstring>
#define ll long long
const ll mod=1e9+7;
int n,t;
struct matrix
{
ll dx[4][4];
matrix()
{
memset(dx,0,sizeof(dx));
}
matrix friend operator *(matrix n1,matrix n2)
{
matrix n3;
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++)
n3.dx[i][j]=(n3.dx[i][j]+n1.dx[i][k]*n2.dx[k][j])%mod;
return n3;
}
}f,d,ans;
void quick(int k)
{
while(k)
{
if(k&1)
f=f*d;
d=d*d;
k>>=1;
}
}
void init()
{
ans.dx[1][1]=1,ans.dx[1][2]=1,ans.dx[1][3]=1;
ans.dx[2][1]=0,ans.dx[2][2]=0,ans.dx[2][3]=0;
ans.dx[3][1]=0,ans.dx[3][2]=0,ans.dx[3][3]=0;
f.dx[1][1]=1,f.dx[1][2]=0,f.dx[1][3]=0;
f.dx[2][1]=0,f.dx[2][2]=1,f.dx[2][3]=0;
f.dx[3][1]=0,f.dx[3][2]=0,f.dx[3][3]=1;
d.dx[1][1]=1,d.dx[1][2]=1,d.dx[1][3]=0;
d.dx[2][1]=0,d.dx[2][2]=0,d.dx[2][3]=1;
d.dx[3][1]=1,d.dx[3][2]=0,d.dx[3][3]=0;
}
void work()
{
scanf("%d",&t);
while(t--)
{
init();
scanf("%d",&n);
if(n>3)
{
quick(n-3);
ans=ans*f;
printf("%d\n",ans.dx[1][1]);
}
else
printf("1\n");
}
}
int main()
{
work();
return 0;
}
2017.7.2


