洛谷 P1361 小M的作物 解题报告
P1361 小M的作物
题目描述
小M在MC里开辟了两块巨大的耕地\(A\)和\(B\)(你可以认为容量是无穷),现在,小\(P\)有\(n\)中作物的种子,每种作物的种子有1个(就是可以种一棵作物)(用1...\(n\)编号)。
现在,第\(i\)种作物种植在\(A\)中种植可以获得\(a_i\)的收益,在\(B\)中种植可以获得\(b_i\)的收益,而且,现在还有这么一种神奇的现象,就是某些作物共同种在一块耕地中可以获得额外的收益,小\(M\)找到了规则中共有\(m\)种作物组合,第\(i\)个组合中的作物共同种在\(A\)中可以获得\(c1_i\)的额外收益,共同总在B中可以获得\(c2_i\)的额外收益。
小M很快的算出了种植的最大收益,但是他想要考考你,你能回答他这个问题么?
输入输出格式
输入格式:
第一行包括一个整数\(n\)
第二行包括\(n\)个整数,表示\(a_i\)第三行包括\(n\)个整数,表示\(b_i\)第四行包括一个整数\(m\)接下来\(m\)行,
对于接下来的第\(i\)行:第一个整数\(k_i\),表示第\(i\)个作物组合中共有\(k_i\)种作物,
接下来两个整数\(c1_i\),\(c2_i\),接下来\(k_i\)个整数,表示该组合中的作物编号。
输出格式:
只有一行,包括一个整数,表示最大收益
数据范围
1<=k< n<= 1000,0 < m < = 1000 保证所有数据及结果不超过\(2*10^9\)。
这个题加深了我对最小割模型的理解。
我第一点弄明白的一点,也是最重要的一点。
最小割在数值上与最大流相等,但在本身性质上与网络流无任何关系。
它的不那么准确的定义是:在一个图中,割去权值和最小的边集,使这个图分成两个部分,切下来的那一刀叫做最小割。最小割并不唯一,但它在数值上是等于最大流的。
对于这个题的模型来说,它有一个名字叫做二者取一式问题,在具体题目中的体现即为把点集一分为二。
类似的题目有善意的投票
虽然说了最小割与网络流无关系,但只是在定义或者说是意义上,真正要到建模时,还需要将两者综合考虑。
先考虑没有额外收益情况下的建图。
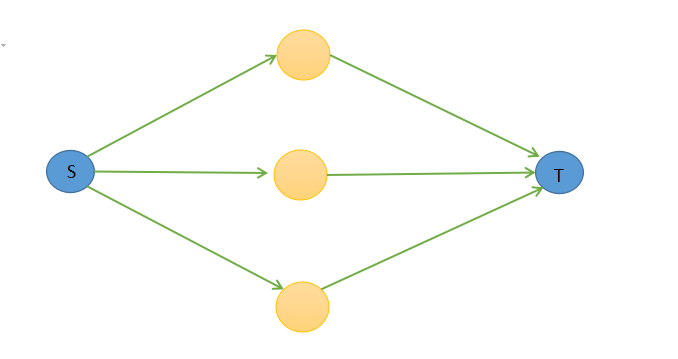
设源点S属于集合A,汇点T属于集合B,则显然点与源点所连的有向边为这个点归属于集合A所产生的收益,与汇点相连则同理。则原图边权之和-最小割就是本题的答案了。
在这个图的基础上,考虑如何把点集给加入。
首先明确一点,点集的贡献有三种情况,对集合A贡献,对集合B贡献或者不贡献。这意味着只划分出一种状态是无法描述的,至少要把A与B的情况分开描述。
讨论一个对\(A\)有贡献的点集\(\{c,d\}\)。
依据题目,我们对这个点集的要求是,只要\(c,d\)有一个点被割到了集合\(T\),这个点集都无法产生贡献。换而言之,只要\(c\)或\(d\)在集合\(B\),代表点集贡献的边必须要断开。
先尝试着连接这条贡献边,因为这条边不可能直接连到图中代表作物的点上,所以连接一个虚点上去。
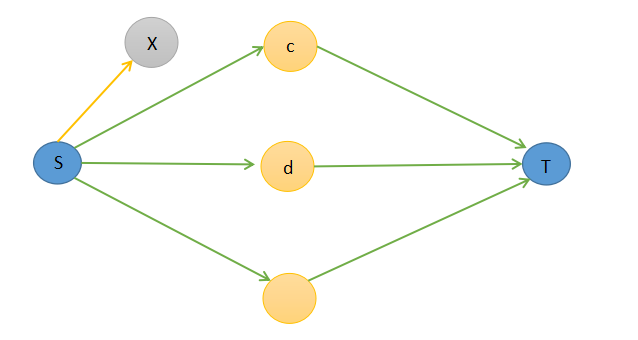
X为点集所产生的虚点。
如果\(c\)被割到了集合\(B\),则所有从\(S\)到\(c\)的路径都得被断开(具体只路径的一条边断掉),如果我们想要黄边断掉,那么虚点\(X\)连\(c\)的那条路径不能被断掉。而容量为正无穷的边不可能被断掉,于是我们这样建图。
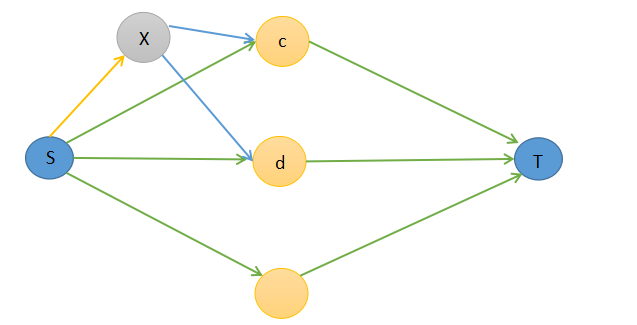
两条蓝色的边的边权为\(inf\)
对待贡献\(B\)集合的点,同理
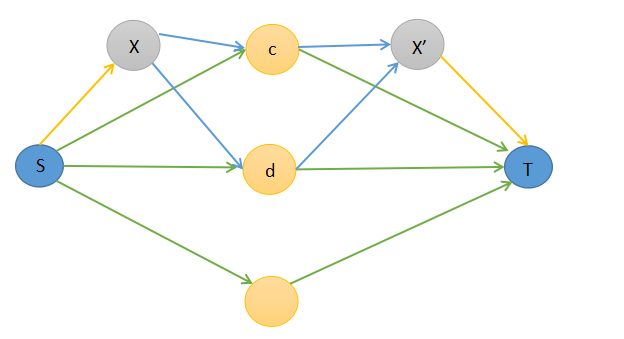
建图跑网络流即可。
要注意的一点是,这题卡常,吸氧才水过去的
Code
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N=3010;
const int M=2000100;
const int inf=0x3f3f3f3f;
int head[N],edge[M],to[M],next[M],cnt=1;
void add(int u,int v,int w)
{
to[++cnt]=v;next[cnt]=head[u];edge[cnt]=w;head[u]=cnt;
to[++cnt]=u;next[cnt]=head[v];edge[cnt]=0;head[v]=cnt;
}
int dep[N],used[N],pre[N],tot,s[N],ans,m,n,sum;
queue <int > q;
bool bfs()
{
while(!q.empty()) q.pop();
q.push(0);
memset(dep,0,sizeof(dep));
dep[0]=1;
while(!q.empty()&&q.front()!=n+1)
{
int u=q.front();
q.pop();
for(int i=head[u];i;i=next[i])
{
int v=to[i],w=edge[i];
if(!dep[v]&&w)
{
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return !q.empty();
}
int main()
{
scanf("%d",&n);
int w,v,k,c1,c2;
for(int i=1;i<=n;i++)
{
scanf("%d",&w);
sum+=w;
add(0,i,w);
}
for(int i=1;i<=n;i++)
{
scanf("%d",&w);
sum+=w;
add(i,n+1,w);
}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&k,&c1,&c2);
add(0,i+n+1,c1);sum+=c1;
add(i+n+m+1,n+1,c2);sum+=c2;
for(int j=1;j<=k;j++)
{
scanf("%d",&v);
add(i+n+1,v,inf);
add(v,i+n+m+1,inf);
}
}
while(bfs())
{
memset(used,0,sizeof(used));
s[++tot]=0;
while(tot)
{
int u=s[tot];
if(u==n+1)
{
int mi=inf,id;
for(int i=tot;i>1;i--)
if(mi>=edge[pre[s[i]]])
{
mi=edge[pre[s[i]]];
id=i;
}
ans+=mi;
for(int i=tot;i>1;i--)
{
edge[pre[s[i]]]-=mi;
edge[pre[s[i]]^1]+=mi;
}
tot=id-1;
used[n+1]=0;
}
else
{
for(int i=head[u];i;i=next[i])
{
int v=to[i],w=edge[i];
if(!used[v]&&dep[v]==dep[u]+1&&w)
{
used[v]=1;
s[++tot]=v;
pre[v]=i;
break;
}
}
if(u==s[tot]) tot--;
}
}
}
printf("%d\n",sum-ans);
return 0;
}
2018.6.28

