洛谷 P3629 [APIO2010]巡逻 解题报告
P3629 [APIO2010]巡逻
题目描述
在一个地区中有 n 个村庄,编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄,每条道路刚好连接两个村庄,从任何一个村庄,都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全,巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里,每天巡警车总是从警察局出发,最终又回到警察局。 下图表示一个有 8 个村庄的地区,其中村庄用圆表示(其中村庄 1 用黑色的 圆表示),道路是连接这些圆的线段。为了遍历所有的道路,巡警车需要走的距 离为 14 个单位,每条道路都需要经过两次。

为了减少总的巡逻距离,该地区准备在这些村庄之间建立 K 条新的道路, 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 (见下面的图例(c))。 一条新道路甚至可以是一个环,即,其两端连接到同一 个村庄。 由于资金有限,K 只能是 1 或 2。同时,为了不浪费资金,每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子:

在(a)中,新建了一条道路,总的距离是 11。在(b)中,新建了两条道路,总 的巡逻距离是 10。在(c)中,新建了两条道路,但由于巡警车要经过每条新道路 正好一次,总的距离变为了 15。 试编写一个程序,读取村庄间道路的信息和需要新建的道路数,计算出最佳 的新建道路的方案使得总的巡逻距离最小,并输出这个最小的巡逻距离。
输入输出格式
输入格式:
第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行,每行两个整数 a, b, 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。
输出格式:
输出一个整数,表示新建了 K 条道路后能达到的最小巡逻距离。
说明
10%的数据中,n ≤ 1000, K = 1;
30%的数据中,K = 1;
80%的数据中,每个村庄相邻的村庄数不超过 25;
90%的数据中,每个村庄相邻的村庄数不超过 150;
100%的数据中,3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。
遇到这种题当然选择手玩数据啦
我们发现:对于初始的树,每条边得经过两次,当连出一个环时,环上的边全都只经过了一次。
那么k=1的30分就拿到了,求出树的直径,统计答案即可。
k=2时,网上大多数的做法是把直径上的边权置-1再求一遍直径,我提供一种大同小异却麻烦一点的做法(可能对我来说比较好想吧)
对链上的每个点,我们以它为根做一遍树的直径,不经过直径上的点,统计出这颗子树的直径和它的最大深度。
直径可以直接更新答案,但这样并不全,可能会有以下一种情况
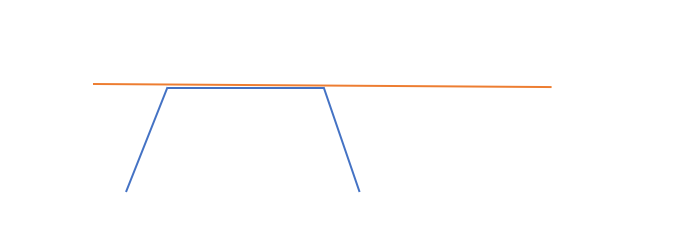
黄链为直径,而紫链为第二次连出的环。
最大深度就在这时候用一下,从左至右扫描一遍直径,用单调队列维护当前最优深度(记得减去原本在直径上的边),更新答案即可
Code:
#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
const int N=100010;
int head[N],to[N<<1],next[N<<1],F[N],cnt,dis[N],mx,mxl,l,r,n,k,q[N][2],is[N],f[N];
void add(int u,int v)
{
to[++cnt]=v;next[cnt]=head[u];head[u]=cnt;
}
void dfs1(int now,int len,int fa)
{
if(len>mxl)
{
l=now;
mxl=len;
}
for(int i=head[now];i;i=next[i])
{
int v=to[i];
if(!is[v]&&fa!=v)
dfs1(v,len+1,now);
}
}
void dfs2(int now,int len,int fa)
{
if(mx<len)
{
r=now;
mx=len;
}
for(int i=head[now];i;i=next[i])
{
int v=to[i];
if(!is[v]&&fa!=v)
{
f[v]=now;
dfs2(v,len+1,now);
}
}
}
void get_d(int s)
{
mx=0,mxl=0,l=0,r=0;
dfs1(s,0,0);
is[s]=0;
dfs2(l,0,0);
is[s]=1;
}
int main()
{
scanf("%d%d",&n,&k);
int u,v;
for(int i=1;i<n;i++)
{
scanf("%d%d",&u,&v);
add(u,v),add(v,u);
}
get_d(1);
is[1]=0;
int L=l,R=r,D=mx,ans=0;
if(k>1)
{
int now=R;
while(now)
{
is[now]=1;
F[now]=f[now];
now=f[now];
}
for(int i=1;i<=n;i++)
if(is[i])
{
get_d(i);
dis[i]=mxl;
ans=max(ans,mx);
}
now=R;
int cntt=1,ll=1,rr=0;
memset(q,-0x3f,sizeof(q));
while(now)
{
if(ll<=rr)
ans=max(ans,q[ll][0]-cntt+q[ll][1]+dis[now]);
while(ll<=rr&&dis[now]>=q[ll][0]-cntt+q[ll][1]) ll++;
q[++rr][0]=dis[now],q[rr][1]=cntt;
cntt++;
now=F[now];
}
}
ans+=D;
printf("%d\n",(n-1<<1)+k-ans);
return 0;
}
2018.6.28


