洛谷 P1852 [国家集训队]跳跳棋 解题报告
P1852 [国家集训队]跳跳棋
题目描述
跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。
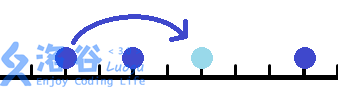
我们用跳跳棋来做一个简单的游戏:棋盘上有3颗棋子,分别在\(a\),\(b\),\(c\)这三个位置。我们要通过最少的跳动把他们的位置移动成\(x\),\(y\),\(z\)。(棋子是没有区别的)
跳动的规则很简单,任意选一颗棋子,对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。
写一个程序,首先判断是否可以完成任务。如果可以,输出最少需要的跳动次数。
输入输出格式
输入格式:
第一行包含三个整数,表示当前棋子的位置\(a\) \(b\) \(c\)。(互不相同)
第二行包含三个整数,表示目标位置\(x\) \(y\) \(z\)。(互不相同)
输出格式:
如果无解,输出一行\(NO\)。
如果可以到达,第一行输出\(YES\),第二行输出最少步数。
说明
20% 输入整数的绝对值均不超过10
40% 输入整数的绝对值均不超过10000
100% 绝对值不超过10^9
精巧的建模题。
划重点了划重点了一次只允许跳过1颗棋子,这句话是解题的关键。
手玩一下跳法,现有描述位置的递增三元组\((x,y,z)\),研究它能够在一步之内跳到何处。
首先,中间的元素可以随意往两边跳到达状态\((2x-y,x,z)\)和状态\((x,z,2z-y)\),注意到这两个三元组的边界是扩大了的。
对于两边的元素,设\(d1=y-x,d2=z-y\)
若\(d1>d2\),则\(c\)可以往内跳,到达状态\((x,b-d2,b)\)
若\(d2>d1\),同理。
注意到这次到达的状态三元组的边界是缩小了的,且跳法具有唯一性
若\(d1=d2\),则边界没法缩小了,假定为边界条件。
对缩小边界的跳法具有唯一性这一性质,我们可以联想到什么呢?
将初始状态和目标状态同时缩小边界,看能否产生交集。
用树来描述这一个状态集合(树父亲的唯一性对应缩小边界的唯一性)。
到这里40分就拿到了。
但是我们发现,树的状态太多,无法存储。
只能每次在线询问需要的状态,复杂度为\(O(d)\),\(d\)的两个节点的相对深度。
感觉这样就像裸奔,所以,能不能降低询问状态的复杂度呢?
再选一个三元组\((x,y,z)\)玩,现在我们只需要它缩小边界的状态了,只玩这个。
对于两边的元素,设\(d1=y-x,d2=z-y\)
只讨论\(d1>d2\)的情况,如下图
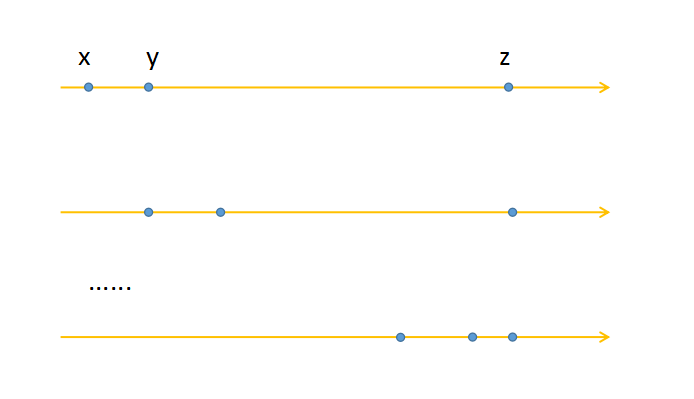
这样看,取一下模,就可以直接到达右边的状态了
当然注意一下细节,比如刚好整除的状态。
参考GCD的复杂度,单次查询差不多最坏为\(O(logD)\),\(D\)为原始给出坐标最大距离
有这个加速,我们基本就只用考虑要怎么询问状态了。
我们尽可能想办法只询问需要的状态。
判断是否能够到达很简单,只需要检验一下两个初始三元组的树根是否一样就行了。
如果在同一颗树了,问题就有点像LCA了。
事实上一开始的一种想法应该是直接加速的模拟往上跳,但实现起来有点困难,跳过了也不太好弄。
有一种倍增求LCA的方式是先把两个点跳到同一深度,然后两个点一起向上跳。
可以仿造这种做法先将两个状态置于一个深度,然后二分它们的LCA离它们的距离,每次加速的往上跳。
于是总复杂度:\(O(log^2D)\)
Code:
#include <cstdio>
#include <algorithm>
int min(int x,int y){return x<y?x:y;}
int r[3],ori[3],goa[3];
int get(int a,int b,int c)
{
int d1=b-a,d2=c-b,cnt=0;
if(d1>d2)
{
cnt=d1/d2;
int d=d1%d2;
if(!d)
{
d+=d2;
cnt--;
}
cnt+=get(a,a+d,a+d+d2);
}
else if(d1<d2)
{
cnt=d2/d1;
int d=d2%d1;
if(!d)
{
d+=d1;
cnt--;
}
cnt+=get(c-d-d1,c-d,c);
}
else
r[0]=a,r[1]=b,r[2]=c;
return cnt;
}
void up(int a,int b,int c,int step)
{
if(!step)
{
r[0]=a,r[1]=b,r[2]=c;
return;
}
int d1=b-a,d2=c-b,cnt=0;
if(d1>d2)
{
cnt=d1/d2;
int d=d1%d2;
if(!d)
{
d+=d2;
cnt--;
}
if(step>=cnt)
up(a,a+d,a+d+d2,step-cnt);
else
{
int k=cnt-step;
up(a,a+d+k*d2,a+d+(k+1)*d2,0);
}
}
else if(d1<d2)
{
cnt=d2/d1;
int d=d2%d1;
if(!d)
{
d+=d1;
cnt--;
}
if(step>=cnt)
up(c-d-d1,c-d,c,step-cnt);
else
{
int k=cnt-step;
up(c-d-(k+1)*d1,c-d-k*d1,c,0);
}
}
else
r[0]=a,r[1]=b,r[2]=c;
}
bool check(int step)
{
int to[3];
up(goa[0],goa[1],goa[2],step);
to[0]=r[0];to[1]=r[1];to[2]=r[2];
up(ori[0],ori[1],ori[2],step);
if(to[0]!=r[0]||to[1]!=r[1]||to[2]!=r[2])
return false;
return true;
}
int main()
{
int to[3],ans=0;
scanf("%d%d%d%d%d%d",ori,ori+1,ori+2,goa,goa+1,goa+2);
std::sort(ori,ori+3);std::sort(goa,goa+3);
int step1=get(ori[0],ori[1],ori[2]);
to[0]=r[0];to[1]=r[1];to[2]=r[2];
int step2=get(goa[0],goa[1],goa[2]);
if(to[0]!=r[0]||to[1]!=r[1]||to[2]!=r[2])
{
printf("NO\n");
return 0;
}
if(step1<step2)
{
ans+=step2-step1;
up(goa[0],goa[1],goa[2],step2-step1);
goa[0]=r[0];goa[1]=r[1];goa[2]=r[2];
}
else if(step1>step2)
{
ans+=step1-step2;
up(ori[0],ori[1],ori[2],step1-step2);
ori[0]=r[0];ori[1]=r[1];ori[2]=r[2];
}
int l=0,rr=min(step1,step2);
while(l<rr)
{
int mid=l+rr>>1;
if(check(mid))
rr=mid;
else
l=mid+1;
}
printf("YES\n%d\n",(l<<1)+ans);
return 0;
}
2018.6.27

