洛谷 P1310 表达式的值 解题报告

P1310 表达式的值

题目描述

对于1 位二进制变量定义两种运算：

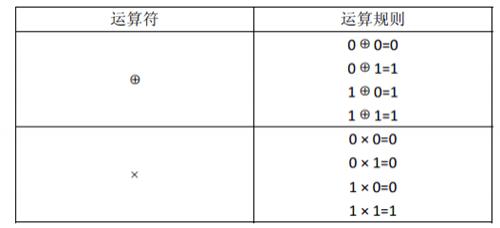
运算的优先级是：

1. 先计算括号内的，再计算括号外的。

2. “× ”运算优先于“⊕”运算，即计算表达式时，先计算× 运算，再计算⊕运算。

例如：计算表达式A⊕B × C时，先计算 B × C，其结果再与 A 做⊕运算。

现给定一个未完成的表达式，例如_+(*)，请你在横线处填入数 0或者1 ，请问有多少种填法可以使得表达式的值为0 。

输入输出格式

输入格式：

共 2 行。

第1 行为一个整数L ，表示给定的表达式中除去横线外的运算符和括号的个数。

第2 行为一个字符串包含L个字符，其中只包含’（’、’）’、’+’、’’这 4 种字符，其中’（’、’）’是左右括号，’+’、’’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。

输出格式：

共1 行。包含一个整数，即所有的方案数。注意：这个数可能会很大，请输出方案数对 10007取模后的结果。

数据范围

对于 20% 的数据有 0≤L≤10 。

对于 50% 的数据有 0≤L≤1,000 。

对于 70% 的数据有 0≤L≤10,000 。

对于 100% 的数据有 0≤L≤100,000 。

对于 50% 的数据输入表达式中不含括号。

---

这题我搞了三个小时（太菜了）

把先前的错误思路统计一下把。

wrong solution1：中缀转后缀，按顺序作DP。发现破坏了式子的性质，得了30分

wrong solution2：栈模拟，同时存储符号和数字，遇到乘号就做（我可能忘记了括号emmmm），50分

正解：栈模拟，同时存储括号和数字，将符号和数字交替插入（两个左括号间不加），遇到右括号求解只含“+”和“*”的式子，求解方法同wrong solution2。记得多模以免爆精度。

公式自己手推一下应该不算难，注意细节。

还有一种做法是笛卡尔树建树+树形DP

---

Code：

#include <cstdio>
const int N=100010;
const int mod=10007;
int tot,tot2,n;
struct node
{
    int ans[2];
    char c;
}s[N],s2[N];
char c[N];
void add()
{
    s[++tot].ans[0]=1,s[tot].ans[1]=1;
}
void put(char cha)
{
    s[++tot].c=cha;
    s[tot].ans[0]=s[tot].ans[1]=0;
}
void get()
{
    tot2=0;
    int a[2];
    while(s[tot].c!='(')
    {
        if(s[tot].ans[0])
            s2[++tot2]=s[tot--];
        else if(s[tot].c=='*')
        {
            tot--;
            a[0]=((s2[tot2].ans[0]*(s[tot].ans[0]+s[tot].ans[1]))%mod+(s2[tot2].ans[1]*s[tot].ans[0])%mod)%mod;
            s2[tot2].ans[1]=(s[tot].ans[1]*s2[tot2].ans[1])%mod;
            s2[tot2].ans[0]=a[0];
            tot--;
        }
        else
            tot--;
    }
    s[tot].ans[1]=s2[1].ans[1];
    s[tot].ans[0]=s2[1].ans[0];
    for(int i=2;i<=tot2;i++)
    {
        a[1]=((s[tot].ans[0]*s2[tot2].ans[1])%mod+(s[tot].ans[1]*(s2[tot2].ans[0]+s2[tot2].ans[1]))%mod)%mod;
        s[tot].ans[0]=(s2[i].ans[0]*s[tot].ans[0])%mod;
        s[tot].ans[1]=a[1];
    }
    s[tot].c=0;
}
void work()
{
    for(int i=0;i<=n;i++)
    {
        if(c[i]!=')')
        {
            if(!s[tot].ans[0]&&c[i]!='(')
                add();
            put(c[i]);
        }
        else
        {
            if(!s[tot].ans[0])
                add();
            get();
        }
    }
}
int main()
{
    scanf("%d",&n);
    scanf("%s",c+1);
    c[0]='(',c[++n]=')';
    work();
    printf("%d\n",s[tot].ans[0]);
    return 0;
}