蒜头君打地鼠
蒜头君打地鼠
题目描述
蒜头君最近迷上了打地鼠,但他发现同时出现在面板上的地鼠太多,于是他想改进一下他的锤子,于是他拿出了一款 k×k 大小的正方形锤子,但是遗憾的是,这个锤子只能斜着砸。如下图所示:
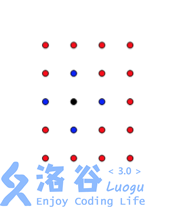
当 k=2 时,若蒜头君敲击黑点,黑点和图中所有蓝色点将一并被敲到。
当 k=3时,锤子的图案如下所示:

k 取其他值时以此类推。
注意:蒜头君只能敲击面板上的格子,但锤子不一定要全部落在面板内。
现在给定一个 n×n 的面板,每个格子可能有地鼠也可能没有地鼠,请编程计算用 k×k 大小锤子敲击时最多能打中多少地鼠。
输入输出格式
输入格式:
第一行 2 个整数 n,k,表示面板大小和锤子大小。
接下来 n行,每行 n 个整数,若为 1 代表该格子有地鼠,若为 0 代表该格子无地鼠。不会出现其他的数字。
输出格式:
输出一个整数,代表最多能砸到的地鼠数。
说明
对于 50% 的测试数据,满足1≤n≤300,1≤k≤10;
对于 80% 的测试数据,满足1≤n≤2000,1≤k≤10;
对于 100% 的测试数据,满足 1≤n≤2000,1≤k≤100。
这两天被对角线前缀和玩死了。。
将原图翻转

蓝色的为原图,斜着看的为新图,对应的坐标画图玩一玩就出来了
注意如果直接统计新图以某点为右下角的正方形数量,有些点是不需要的。
code:
#include <cstdio>
int max(int x,int y){return x>y?x:y;}
const int N=4010;
int f[N][N],n,k;
int cali(int i,int j)
{
return i+j-1;
}
int calj(int i,int j)
{
return n+j-i;
}
int cal(int i,int j)
{
return f[i][j]-(i>=k?f[i-k][j]:0)-(j>=k?f[i][j-k]:0)+(i>=k&&j>=k?f[i-k][j-k]:0);
}
int main()
{
scanf("%d%d",&n,&k);
int w;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
scanf("%d",&w);
int i0=cali(i,j);
int j0=calj(i,j);
f[i0][j0]=w;
}
n=(n<<1)-1,k=(k<<1)-1;
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1];
int typ=!(((n+1>>1)&1)^1);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if((i&1)^(j&1)^typ)
ans=max(ans,cal(i,j));
int d=cal(5,5);
printf("%d\n",ans);
return 0;
}
2018.6.23


