洛谷 P1070 道路游戏 解题报告
P1070 道路游戏
题目描述
小新正在玩一个简单的电脑游戏。
游戏中有一条环形马路,马路上有\(n\)个机器人工厂,两个相邻机器人工厂之间由一小段马路连接。小新以某个机器人工厂为起点,按顺时针顺序依次将这\(n\)个机器人工厂编号为\(1-n\),因为马路是环形的,所以第\(n\)个机器人工厂和第\(1\)个机器人工厂是由一段马路连接在一起的。小新将连接机器人工厂的这\(n\)段马路也编号为\(1-n\),并规定第\(i\)段马路连接第\(i\)个机器人工厂和第\(i+1\)个机器人工厂(\(1≤i≤n-1\)),第\(n\)段马路连接第\(n\)个机器人工厂和第1个机器人工厂。
游戏过程中,每个单位时间内,每段马路上都会出现一些金币,金币的数量会随着时间发生变化,即不同单位时间内同一段马路上出现的金币数量可能是不同的。小新需要机器人的帮助才能收集到马路上的金币。所需的机器人必须在机器人工厂用一些金币来购买,机器人一旦被购买,便会沿着环形马路按顺时针方向一直行走,在每个单位时间内行走一次,即从当前所在的机器人工厂到达相邻的下一个机器人工厂,并将经过的马路上的所有金币收集给小新,例如,小新在\(i\)(\(1≤i≤n\))号机器人工厂购买了一个机器人,这个机器人会从\(i\)号机器人工厂开始,顺时针在马路上行走,第一次行走会经过\(i\)号马路,到达\(i+1\)号机器人工厂(如果\(i=n\),机器人会到达第1个机器人工厂),并将\(i\)号马路上的所有金币收集给小新。 游戏中,环形马路上不能同时存在\(2\)个或者\(2\)个以上的机器人,并且每个机器人最多能够在环形马路上行走\(p\)次。小新购买机器人的同时,需要给这个机器人设定行走次数,行走次数可以为\(1~p\)之间的任意整数。当马路上的机器人行走完规定的次数之后会自动消失,小新必须立刻在任意一个机器人工厂中购买一个新的机器人,并给新的机器人设定新的行走次数。
以下是游戏的一些补充说明:
游戏从小新第一次购买机器人开始计时。
购买机器人和设定机器人的行走次数是瞬间完成的,不需要花费时间。
购买机器人和机器人行走是两个独立的过程,机器人行走时不能购买机器人,购买完机器人并且设定机器人行走次数之后机器人才能行走。
在同一个机器人工厂购买机器人的花费是相同的,但是在不同机器人工厂购买机器人的花费不一定相同。
购买机器人花费的金币,在游戏结束时再从小新收集的金币中扣除,所以在游戏过程中小新不用担心因金币不足,无法购买机器人而导致游戏无法进行。也因为如此,游戏结束后,收集的金币数量可能为负。
现在已知每段马路上每个单位时间内出现的金币数量和在每个机器人工厂购买机器人需要的花费,请你告诉小新,经过 mm 个单位时间后,扣除购买机器人的花费,小新最多能收集到多少金币。
输入输出格式
输入格式:
第一行3个正整数\(n,m,p\),意义如题目所述。
接下来的\(n\)行,每行有\(m\)个正整数,每两个整数之间用一个空格隔开,其中第\(i\)行描
述了\(i\)号马路上每个单位时间内出现的金币数量(1≤ 金币数量 ≤100),即第\(i\)行的第\(j\)( \(1≤j≤m\))个数表示第\(j\)个单位时间内\(i\)号马路上出现的金币数量。
最后一行,有\(n\)个整数,每两个整数之间用一个空格隔开,其中第\(i\)个数表示在\(i\)号机器人工厂购买机器人需要花费的金币数量( 1≤ 金币数量 ≤100 )。
输出格式:
共一行,包含1个整数,表示在\(m\)个单位时间内,扣除购买机器人
花费的金币之后,小新最多能收集到多少金币。
说明
对于 40%的数据, 2≤n≤40,1≤m≤40 。
对于 90%的数据, 2≤n≤200,1≤m≤200。
对于 100%的数据, 2≤n≤1000,1≤m≤1000,1≤p≤m。
NOIP 2009 普及组 第四题
写这个题真是累啊,好毒。应该练练处理比较麻烦的DP。
在读完题目以后,其实初始版的方程并不难想
\(dp[i][j][k]\)表示时间\(i\)在工厂\(j\)当机器人前已经走了\(k\)步的方案。
\(k\)那一维可以通过直接枚举消去
\(dp[i][j][1/0]\)表示时间\(i\)工厂\(j\)是否能够继续再走
转移为
\(dp[i][j][1]=max(dp[i][j][1],dp[i-k][j-k][0]+cal(i,j,k))\)//没有列出关于环的情况的,以下会详细说
\(dp[i][j][0]=max(dp[i][j][0],dp[i][k][1]-cost[j])\)
确实很不完美,我当时也只是想到了这么多,感觉过个90还是比较轻松的,1000的点拿单调队列优化一下就行了。
然后我就开始写\(cal\)函数,处理那个对角线式的前缀和,然后成功把自己搅糊了。
这个题把点权释放到了边权上,人话就是存储的路径位置其实是某个点伸出去的那一条

比如用这个图来描述读入的某时间某费用数组
\(f[i][j]\)表示时间\(i\)位置\(j\)所延伸回去的45°的链的值,如下图,黄点为\((i,j)\)的位置,则它所代表的链为蓝色的一条链上的点权之和。
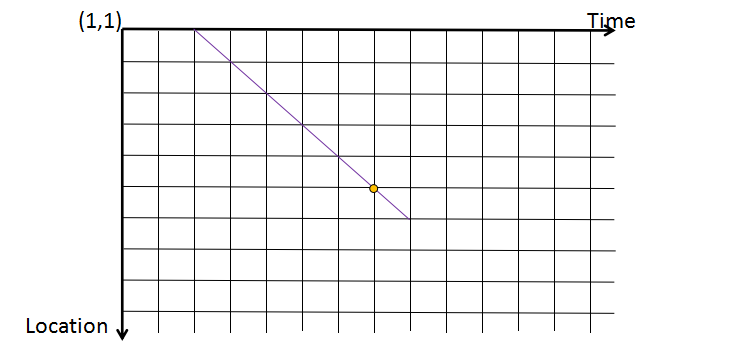
好吧,弄清楚了这个,写一下\(cal(i,j,k)\)函数了,如下图,它要返回这样一个链的值
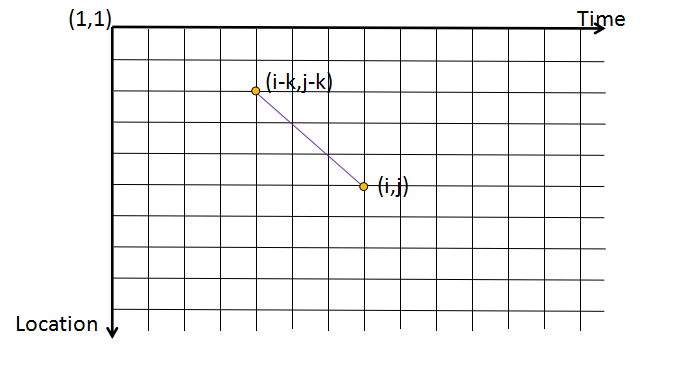
事实上看起来也不是那么麻烦
int cal(int i,int j,int k)
{
return f[i-1][j-1]-f[i-k-1][j-k-1];
}
但是,当转移设计到拐弯时
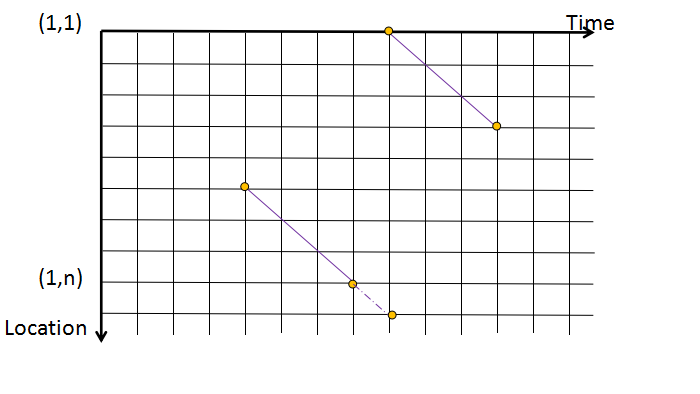
确实有点麻烦。。。我最开始漏掉了那条虚线。。
这是带拐弯的转移:\(dp[i][j][1]=max(dp[i][j][1],dp[i-k][n+j-k][0]+cal(i-j+1,n+1,k-j+1)+cal(i,j,j-1))\)
好吧,到这里我已经感觉我写不出单调队列了。
交了一下果然拿到了90分,其实在如果在考场上做到这里已经可以了(鬼知道为什么部分分有这么多)
部分分代码:
#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
int min(int x,int y){return x<y?x:y;}
const int N=1010;
const int inf=0x3f3f3f3f;
int dp[N][N][2],n,m,p,harv[N][N],f[N][N],cost[N],ans=-inf;//n数量,m时间
int cal(int i,int j,int k)
{
return f[i-1][j-1]-f[i-k-1][j-k-1];
}
int main()
{
memset(dp,-0x3f,sizeof(dp));
scanf("%d%d%d",&n,&m,&p);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&harv[i][j]);
f[j][i]=f[j-1][i-1]+harv[i][j];
}
for(int i=1;i<=n;i++)
scanf("%d",cost+i);
for(int i=1;i<=n;i++)
dp[1][i][0]=-cost[i];
m++;
for(int i=2;i<=m;i++)//时间
{
for(int j=1;j<=n;j++)//路程
{
for(int k=1;k<=min(i,p);k++)//从第几个之前转移
{
if(j>k)
dp[i][j][1]=max(dp[i][j][1],dp[i-k][j-k][0]+cal(i,j,k));
else if(i>j)
dp[i][j][1]=max(dp[i][j][1],dp[i-k][n+j-k][0]+cal(i-j+1,n+1,k-j+1)+cal(i,j,j-1));
}
}
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
{
if(k==j) continue;
dp[i][j][0]=max(dp[i][j][0],dp[i][k][1]-cost[j]);
}
}
for(int i=1;i<=n;i++)
ans=max(ans,dp[m][i][1]);
printf("%d\n",ans);
return 0;
}
看看各位佬爷的题解。
才发现自己的方程太不优秀了,优秀的方程\(O(N^3)\)甚至可以卡过。
\(dp[i]\)表示时间\(i\)的最大答案。
转移:\(dp[i]=max(dp[i-k]+cal(i,j,k)-cost[j-k])\)//无环
看着减去的\(cost[i]\),我明白了应该给\(dp[i]\)加一个定语
\(dp[i]\)表示时间\(i\)处在某位置上还未在此位置上消费机器人的最大答案,每一步的机器人花费是在被转移的时候才扣得啊。而我最初的方程,是代表当前时间\(i\)和地点\(j\)已经买了机器人的最大答案。为了区分是否处理花费机器人的状态,我甚至得用第三维的0/1维护。
读了读题目中“必须立刻在 任意 一个机器人工厂中购买一个新的机器人”,我明白了为什么可以不要地点这一维,其实每一个时间都可以当做是步数已经到了的时间,而此时地点的选择是具有任意性的,即此时地点也是不重要的。
我把方程改了改,果然\(O(N^3)\)卡过了
单调队列优化
但是,如果数据再卡一点,单队优化就是必须的了。
在这里,因为实在是觉得这种点权下放的方式不优雅,我将工厂的实际编号和时间给减去了1,而读入时不变
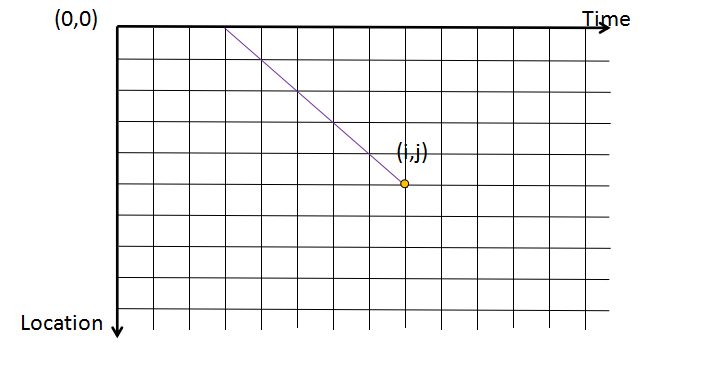
这样,查询\(f[i][j]\)所代表的就不是再多延伸出去一条链了,很舒服了。
再列出转移方程://无环
\(dp[i]=max(dp[i-k]+f[i][j]-f[i-k][j-k]-cost[j-k])\)
\(=max(dp[i-k]-f[i-k][j-k]-cost[j-k])+f[i][j]\)
转移时维护\(q[i][j]=dp[i]-f[i][j]-cost[j]\)即可
因为每一个\(f[i][j]\)都可以唯一的确定一个\(dp[i]\)和\(cost[j]\),所以我们考虑\(f[i][j]\)在转移时的分布。
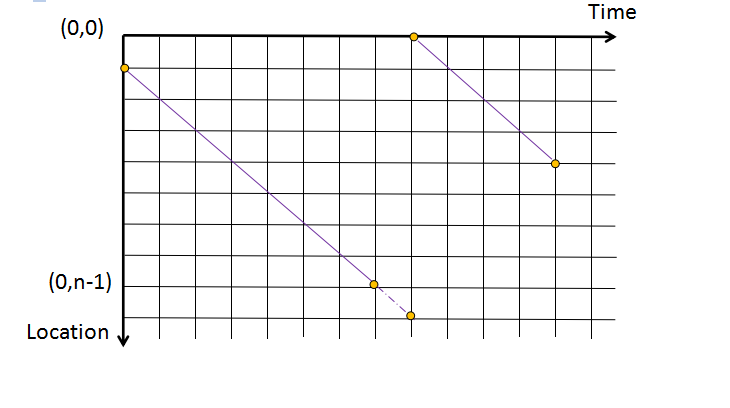
对同一个答案的贡献,这个分布大概是这样。
为了准确的定位某个答案从哪个单调队列转移,考虑给每一个单调队列编号,将单队与\(location\)轴相交的那个点作为它的编号。
在还没拐弯时,所属单队即为\(j-i\),拐弯了以后我们发现它减去了\(l\)个\(n\),\(l\)为拐弯次数,很简单,取膜以后加一个再取膜即可
int get(int i,int j)//获取单队编号
{
return ((j-i)%n+n)%n;
}
还有两点要注意的地方
一是虚线所连的边仍然需要特判一下
二是为了确保拐弯后不出现问题,要把\(dp[i]=max(dp[i-k]-f[i-k][j-k]-cost[j-k])+f[i][j]\)中的\(f[i][j]\)加上它失去的链的长度,维护一个\(add[i]\)数组。
参考代码:
#include <cstdio>
#include <cstring>
const int N=1010;
int max(int x,int y){return x>y?x:y;}
int n,m,p;
int f[N][N],cost[N],q[N][N],loc[N][N],l[N],r[N],add[N],dp[N];
int get(int i,int j)//获取单队编号
{
return ((j-i)%n+n)%n;
}
int main()
{
scanf("%d%d%d",&n,&m,&p);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&f[j][i]);
f[j][i]+=f[j-1][i-1];
}
for(int i=0;i<n;i++)
{
scanf("%d",cost+i);
q[i][++r[i]]=-cost[i],l[i]++;
}
memset(dp,-0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=m;i++)
{
for(int j=0;j<n;j++)
{
int id=get(i,j);
while(l[id]<=r[id]&&loc[id][l[id]]+p<i) l[id]++;
if(!j) add[id]+=f[i][n];
if(l[id]<=r[id])
dp[i]=max(dp[i],q[id][l[id]]+add[id]+f[i][j]);
}
for(int j=0;j<n;j++)
{
int id=get(i,j);
int tmp=dp[i]-add[id]-f[i][j]-cost[j];
while(l[id]<=r[id]&&q[id][r[id]]<=tmp)
r[id]--;
loc[id][++r[id]]=i;
q[id][r[id]]=tmp;
}
}
printf("%d\n",dp[m]);
return 0;
}
2018.6.22


