大奖赛 解题报告

据说是教练从清北食堂捞的题目

大奖赛

题目背景

你不努力，未来别人壁咚的墙都是你砌的！

题目描述

\(Lancelot\)市最近要举办大奖赛拉！住在市里的市民都十分兴奋，\(Morgan\)也不例外。他查了一下比赛的信息，发现比赛一共有\(N\)场，并且每一场的门票价格可能会不相等。\(Morgan\)留给比赛的预算是\(K\)元；他想知道，一共有多少种买票的方案，使得门票之和不超过\(K\)呢？

输入输出格式

输入格式：

第一行两个整数\(N\)与\(K\)，代表比赛的场数和自己的预算。 第二行\(N\)个整数\(A_i\)，代表每场比赛的门票价格。

输出格式：

一行一个整数，代表买票的总方案数。

说明

对于30%的数据，N<=10
对于60%的数据，K<=10000
对于100%的数据，1<=N<=40,0<k,Ai<=1000000000。

---

30% \(O(2^N)\) 暴搜即可

50% \(O(NK)\) 0/1背包

100% \(O(2^{N/2}log2^{N/2})\) 双向搜索

介绍一下双向搜索的方法。

将门票价格分成平均大小的两个集合，分别对两个集合进行枚举并统计答案。

具体实现如下，将其中一个集合所产生的状态用数组存储并排序，当枚举另一个集合得到答案\(cost\)时，在第一个集合产生的答案中进行二分查找（查找\(k-cost\)在之中的前驱位置），得到的位置即为这个\(cost\)产生的答案。

这本质上其实是一种拿空间换时间的方法，把一半所产生的状态进行有序存储，在另一半产生答案时直接二分查找统计。

可以做做这个题，差不多，送礼物

值得一提的是，这个题我也有一点收获，是关于搜索的。

在枚举状态时，如果我们这么枚举

void dfs1(int now,ll cost)
{
    if(cost>k) return;
    if(now==mid+1)
    {
        costa[++cnt]=cost;
        return;
    }
    dfs1(now+1,cost+a[i]);
    dfs2(now+1,cost);
}

那么产生的搜索树是这样的

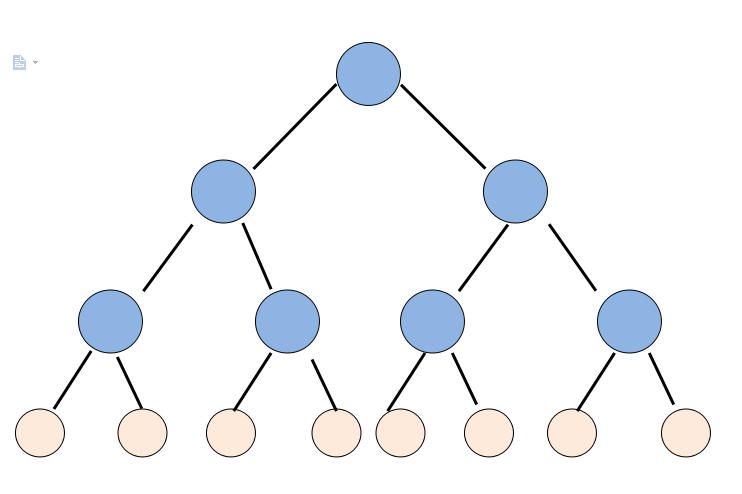
左右子树分别表示这个点选没选

其中，每个粉红色的点所在的链表示一个状态，也就是说，只有叶子节点可以代表状态。这和平常的思路是比较相近的。

但如果这样写

void dfs1(int now,ll cost)
{
    costa[++cnt]=cost;
    for(int i=now+1;i<=mid;i++)
        if(cost+a[i]<=k)
            dfs1(i,cost+a[i]);
}

那么产生的搜索树是这样的

节点标号代表选中的节点在a数组的位置。

这样，每一个节点所代表的链都是一个状态了。

显然，第二种是比较优秀的。

---

code:

#include <cstdio>
#include <algorithm>
#define ll long long
const int N=45;
ll a[N],n,k,costa[1<<21],cnt=0,mid,ans=0;
void dfs1(int now,ll cost)
{
    costa[++cnt]=cost;
    for(int i=now+1;i<=mid;i++)
        if(cost+a[i]<=k)
            dfs1(i,cost+a[i]);
}
void find(ll x)
{
    ll l=1,r=cnt;
    while(l<r)
    {
        ll Mid=l+r+1>>1;
        if(costa[Mid]<=x)
            l=Mid;
        else
            r=Mid-1;
    }
    ans+=l;
}
void dfs2(int now,ll cost)
{
    find(k-cost);
    for(int i=now+1;i<=n;i++)
        if(cost+a[i]<=k)
            dfs2(i,cost+a[i]);
}
int main()
{
    scanf("%lld%lld",&n,&k);
    for(int i=1;i<=n;i++)
        scanf("%lld",a+i);
    mid=n>>1;
    std::sort(a+1,a+1+n);
    dfs1(0,0);
    std::sort(costa+1,costa+1+cnt);
    costa[0]=-1;
    dfs2(mid,0);
    printf("%lld\n",ans);
    return 0;
}

---

2018.6.21