洛谷 P1437 [HNOI2004]敲砖块 解题报告

P1437 [HNOI2004]敲砖块

题目描述

在一个凹槽中放置了 n 层砖块、最上面的一层有n 块砖，从上到下每层依次减少一块砖。每块砖

都有一个分值，敲掉这块砖就能得到相应的分值，如下所示。

14 15 4 3 23
33 33 76 2
2 13 11
22 23
31

如果你想敲掉第 i 层的第j 块砖的话，若i=1，你可以直接敲掉它；若i>1，则你必须先敲掉第

i-1 层的第j 和第j+1 块砖。

你现在可以敲掉最多 m 块砖，求得分最多能有多少。

输入输出格式

输入格式：

输入文件的第一行为两个正整数 n 和m；接下来n 行，描述这n 层砖块上的分值a[i][j],满足

0≤a[i][j]≤100。

对于 100%的数据，满足1≤n≤50，1≤m≤n*(n+1)/2；

输出格式：

输出文件仅一行为一个正整数，表示被敲掉砖块的最大价值总和。

---

最开始感觉不具有无后效性就对着容斥原理糊了一个多小时，思维从有依赖的背包到树上分组背包飘到TOPO+DP上，无果。

但是，对着三角形的非直角做是可以具有无后效性的

比如对如下这个图，从左往右一列一列的做就可以。

令\(dp[i][j][k]\)表示前\(i\)列一共打了\(j\)块砖头并且在第\(i\)列打了\(k\)块砖头的最大得分。

这时候，左边的子小三角形就是独立的了，而直角边显然不行。

转移：
\(dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-k][l]+s[i][k])\),其中\(l\)为枚举的一维，\(s[i][j]\)为前缀和数组。

非常值得注意的是，为了避免如下情况的(即三角形不连续)出现，对每一维选择0块砖头去打的情况我们也要注意到。

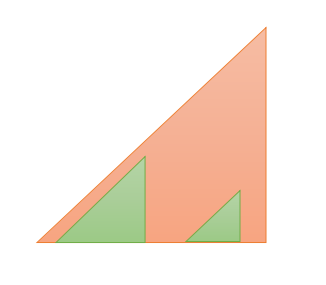
一些上下界的细节也很多，不过多赘述了。

当然，此题也有针对转移的优化，可以将复杂度降到\(O(n^3)\)

---

Code:

#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
int min(int x,int y){return x<y?x:y;}
const int N=52;
int n,m,f[N][N],dp[N][N*N][N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=n;j>=i;j--)
        {
            scanf("%d",&f[i][j]);
            f[i][j]+=f[i-1][j];
        }
    memset(dp,-0x3f,sizeof(dp));
    dp[0][0][0]=0;
    for(int i=1;i<=n;i++)
        for(int j=0;j<=min(m,(i+1)*i/2);j++)//总砖数
            for(int k=0;k<=min(i,j);k++)//当前列选几块
                for(int l=max(0,k-1);l<=i-1;l++)//上一列选几块
                    dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-k][l]+f[k][i]);
    int ans=0;
    for(int i=1;i<=n;i++)
        for(int j=0;j<=i;j++)
            ans=max(ans,dp[i][m][j]);
    printf("%d\n",ans);
    return 0;
}

---

2018.6.19