洛谷 P2680 运输计划 解题报告
P2680 运输计划
题目背景
公元2044年,人类进入了宇宙纪元。
题目描述
公元2044年,人类进入了宇宙纪元。
\(L\)国有\(n\)个星球,还有\(n-1\)条双向航道,每条航道建立在两个星球之间,这\(n−1\)条航道连通了\(L\)国的所有星球。
小\(P\)掌管一家物流公司, 该公司有很多个运输计划,每个运输计划形如:有一艘物流飞船需要从\(u_i\)号星球沿最快的宇航路径飞行到\(v_i\)号星球去。显然,飞船驶过一条航道是需要时间的,对于航道\(j\),任意飞船驶过它所花费的时间为\(t_j\),并且任意两艘飞船之间不会产生任何干扰。
为了鼓励科技创新,\(L\)国国王同意小\(P\)的物流公司参与\(L\)国的航道建设,即允许小\(P\)把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小\(P\)的物流公司就预接了\(m\)个运输计划。在虫洞建设完成后,这\(m\)个运输计划会同时开始,所有飞船一起出发。当这\(m\)个运输计划都完成时,小\(P\)的物流公司的阶段性工作就完成了。
如果小\(P\)可以自由选择将哪一条航道改造成虫洞, 试求出小\(P\)的物流公司完成阶段性工作所需要的最短时间是多少?
输入输出格式
输入格式:
第一行包括两个正整数\(n, m\),表示\(L\)国中星球的数量及小\(P\)公司预接的运输计划的数量,星球从1到\(n\)编号。
接下来\(n-1\)行描述航道的建设情况,其中第\(i\)行包含三个整数\(a_i, b_i\)和\(t_i\)t ,表示第\(i\)条双向航道修建在\(a_i\)与 \(b_i\)两个星球之间,任意飞船驶过它所花费的时间为 \(t_i\) 。数据保证\(1≤a _i ,b_i ≤n\)且\(0≤t_i≤1000\)。
接下来\(m\)行描述运输计划的情况,其中第\(j\)行包含两个正整数\(u_j\)和\(v_j\) ,表示第\(j\)个运输计划是从\(u_j\)号星球飞往\(v_j\)号星球。数据保证\(1≤u_i,v_i≤n\)
输出格式:
一个整数,表示小\(P\)的物流公司完成阶段性工作所需要的最短时间。
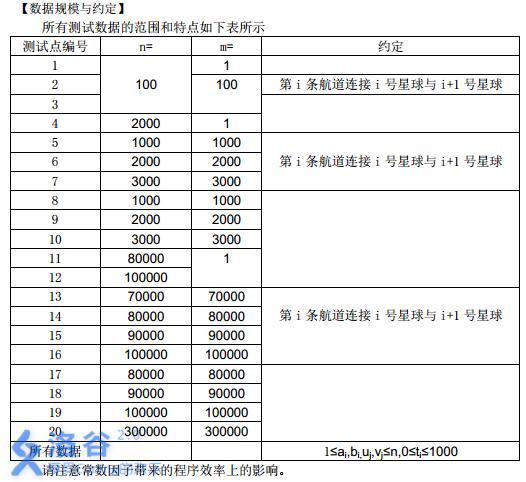
说明:
首先简化一下问题模型:对于询问的m条链中,删去一条边,使最大链最小。
妥妥的二分答案了,但是我做的时候并没有想简化模型,自然也没有想到二分答案,只是想到了贪心倍增的做法但是太难写,我估计写不出来。
下面说说二分答案。我们二分最大链长\(l\)。
对于链长小于等于\(l\)的,我们不管它。
对于链长大于\(l\)的,我们得确保删去的那条边在每条这样的链上,换而言之,我们要统计当前每条边的经历的链数。
我们找到合法的最大边,看看减去它后是否能使所有链长小于\(l\)。
那么现在还有两个问题,如何找到链和如何统计每条边经历的链数。
找到链即先预处理每条链的最近公共祖先,存储为三元组并带上链长。可以用\(tarjan\)直接\(O(n)\)离线处理了
统计链数时,我们发现也是离线操作而且没有修改。直接树上差分即可。
树上差分:思想与链上差分差不多,对三元组\((f,v1,v2)\)(\(f\)是后面两个祖先),维护\(f\)的差分数组减去2,\(v1,v2\)的加上1。自下往上统计前缀和即是边的经历次数。
code:
#include <cstdio>
#include <cstring>
int max(int x,int y){return x>y?x:y;}
const int N=300010;
int n,m;
int read()
{
char c=getchar();int x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
return x;
}
struct Edge{int to,next,w;}edge[N<<1];
struct node{int to,next;}lca[N<<1];
int head[N],cnt=0,headl[N],cntl=0,dis[N],used[N],f[N],l=0,r=0;
void add(int u,int v,int w){edge[++cnt].next=head[u];edge[cnt].to=v;edge[cnt].w=w;head[u]=cnt;}
void addl(int u,int v){lca[++cntl].next=headl[u];lca[cntl].to=v;headl[u]=cntl;}
void dfs(int now)
{
used[now]=1;
for(int i=head[now];i;i=edge[i].next)
{
int v=edge[i].to,w=edge[i].w;
if(!used[v])
{
dis[v]=dis[now]+w;
dfs(v);
}
}
}
int find(int x){return f[x]=f[x]==x?x:find(f[x]);}
void merge(int x,int y){f[find(y)]=find(x);}
struct lc{int v[2],w,next;}d[N];int headlc[N],cntlc=0;
void addlc(int u,int w,int v1,int v2){d[++cntlc].w=w;d[cntlc].v[0]=v1;d[cntlc].v[1]=v2;d[cntlc].next=headlc[u];headlc[u]=cntlc;}
void LCA(int now)
{
used[now]=1;
for(int i=head[now];i;i=edge[i].next)
{
int v=edge[i].to;
if(!used[v])
{
used[v]=1;
LCA(v);
merge(now,v);
}
}
for(int i=headl[now];i;i=lca[i].next)
{
int v=lca[i].to;
if(used[v])
{
int f0=find(v);
int w=dis[v]-dis[f0]+dis[now]-dis[f0];
r=max(r,w);
addlc(f0,w,v,now);
}
}
}
void init()
{
dfs(1);//预处理两点间长度
int a,b;
for(int i=1;i<=m;i++)
{
a=read(),b=read();
addl(a,b);
addl(b,a);
}
memset(used,0,sizeof(used));
for(int i=1;i<=n;i++) f[i]=i;
LCA(1);//两点间距离及最近公共祖先
}
int p_d[N],cntline=0,sum[N],m_max=0,m_maxl=0;
void dfs0(int now,int dist)
{
used[now]=1;
for(int i=head[now];i;i=edge[i].next)
{
int v=edge[i].to,w=edge[i].w;
if(!used[v])
{
dfs0(v,w);
sum[now]+=sum[v];
}
}
sum[now]+=p_d[now];
if(sum[now]==cntline)
m_max=max(m_max,dist);
}
bool check(int c)
{
memset(p_d,0,sizeof(p_d));
cntline=0,m_max=0,m_maxl=0;
for(int i=1;i<=n;i++)
for(int j=headlc[i];j;j=d[j].next)
if(d[j].w>c)
{
p_d[i]-=2;
p_d[d[j].v[0]]++;
p_d[d[j].v[1]]++;
m_maxl=max(m_maxl,d[j].w);
cntline++;
}
memset(used,0,sizeof(used));
memset(sum,0,sizeof(sum));
dfs0(1,0);
return m_max+c>=m_maxl;
}
int main()
{
n=read(),m=read();
int u,v,w;
for(int i=1;i<n;i++)
{
u=read(),v=read(),w=read();
l=max(l,w);
add(u,v,w);
add(v,u,w);
}
l=r-l;
init();
while(l<r)
{
int mid=l+r>>1;
if(check(mid))
r=mid;
else
l=mid+1;
}
printf("%d\n",l);
return 0;
}
其实这个代码\(N\)改成450,000再吸一波氧才能过。但我始终没弄清楚到底\(N\)开300,000到底是哪里\(RE\)了,有哪位大哥发现了评论一下呗~
2018.6.7


