一些我不会证又记不住的结论...

觉得有什么错误的地方烦请提出！

绝对不咕咕咕！！！

k-nim

• k-nim的必败状态：所有子游戏的\(SG\)值的每一位的\(1\)的个数都被\(k+1\)整除

阶梯Nim

$$\color{pink}{link}$$

群论三连

设\(G\)是目标集\([1,n]\)上的一个置换群，\(E_k\)是\([1,n]\)在\(G\)的作用下包含\(k\)的等价类，\(Z_k\)是使\(k\)不动的置换类，\(C(\pi)\)在置换\(\pi\)下目标集的不动点个数，\(m(\pi)\)置换\(\pi\)的循环节个数，\(L\)是目标集等价类的个数

具体点：\(Z_k\)是保持元素\(k\)不变的置换集合，\(E_k\)是\(k\)通过\(G\)中的置换可以得到的元素集合，等价类是元素经过置换可以变成一样的元素集合，可以想象一个无向图的环。

轨道-稳定集定理

\[|E_k|\times |Z_k|=|G| \]

\(Burnside\)定理

\[L=\frac{1}{|G|}\sum_{\pi\in G}C(\pi) \]

• 文字描述：\(1\)到\(N\)在置换群作用下等价类的个数，等于每个置换的不动点个数的平均数。

\(Poly\acute a\)定理

\[L=\frac{1}{|G|}\sum_{\pi \in G}k^{m(\pi)} \]

• \(k\)是可染的颜色数量

一些的并不懂的复杂度证明（积分学的烂

• 枚举\(1-2^n\)每个数的二进制子集

  用这种方法

  for(int s=t;s;s=(s-1)&t)
  

  复杂度：\(O(3^n)\)

• \(O(\sum\limits_{k\mid n}\sqrt k)\)

  \[=O\left( \sum_{1\le i\le \sqrt{n}}{\sqrt{i}+\sqrt{\frac{n}{i}}} \right) =O\left( \int_1^{\sqrt{n}}{dx\left( \sqrt{i}+\sqrt{\frac{n}{i}} \right)} \right) =O\left( \frac{8n^{\frac{3}{4}}}{3} \right) =O\left( n^{\frac{3}{4}} \right) \]

二项式反演

以前没有认真想过，从这个方向对普通容斥套式子可能更加方便。

\[f_n=\sum_{i=0}^n(-1)^i\binom{n}{i}g_i\Leftrightarrow g_n=\sum_{i=0}^n(-1)^i\binom{n}{i}f_i \]

式子的对称性很强，另一个方向可能更加常见

\[f_n=\sum_{i=0}^n\binom{n}{i}g_i\Leftrightarrow g_n=\sum_{i=0}^n(-1)^{i}\binom{n}{i}f_{n-i} \]

后面这个可以卷

---

证明一下第一个式子了口胡开始

具体思路是容斥原理，不涉及代数证明，因为我觉得从组合角度说更便于理解。

设有一个集合\(S\)，其中的每个元素都有若干个性质\(p\)，一共存在\(n\)个性质。

设至少有性质\(p_i\)的元素的集合为\(A_i\)

分别定义：

\[f_i=|A_{p_{c_1}}\bigcap A_{p_{c_2}}\bigcap A_{p_{c_3}}\bigcap \dots\bigcap A_{p_{c_n}}| \]

\[g_i=|A_{p_{c_1}}\bigcup A_{p_{c_2}}\bigcup A_{p_{c_3}}\bigcup \dots\bigcup A_{p_{c_n}}| \]

其中\(\{c\}\)是任意的一个长度固定的递增序列。

容易发现，\(f_i,g_i\)的值并不是定值，所以再添加一个定义，让集合变得特殊一些，让这两个值变成定值就行了。

暴力推式子

\[g_n=|S|-\sum|A_i|+\sum|A_i||A_j|-\dots+(-1)^n\sum|A_1||A_2|\dots|A_n| \]

然后把\(f_i\)带进去

\[g_n=f_0-\binom{n}{1}f_1+\dots+(-1)^n\binom{n}{n}f_n \]

然后推\(f_n\)也是差不多的

原根

若\(g\)是\(m\)(\(m\)是质数)的原根，则\(g^0,g^1,\dots,g^{\varphi(m)-1}\)遍历\(\bmod m\)的最小剩余系。

检验\(g\)是否为原根，把\(m-1\)分解质因数得到每个质因子\(p_i\)，若\(\exists g^{\frac{m-1}{p_i}}\equiv 1 \pmod m\)，则\(g\)不是原根

一般来说我们求原根从\(2\)开始枚举就可以了，因为原根一般比较小。

斯特林数

• 一些公式

\[x ^ n = \sum_k {n \brace k} x ^ {\underline{k}} \]

来个组合的证明吧，会比较舒服。

将\(n\)个有标号球放到\(x\)个有标号的盒子的方案数是\(x^n\)

将\(n\)个有标号球放到\(x\)个有标号的非空盒子的方案数是\({n \brace x}x!\)

那么按照组合的意义有

\[\begin{aligned} x^n&=\sum_{i=0}^x{n\brace i}\binom{x}{i}i!\\ &=\sum_{i=0}^n{n\brace i}\binom{x}{i}i!\\ &=\sum_{i=0}^n {n\brace i}x^{\underline i} \end{aligned} \]

注意这个东西进行二项式反演可以得到一个式子

\[{n \brace k}=\sum_{i=0}^k\frac{(-1)^i}{i!}\frac{(k-i)^n}{(k-i)!} \]

这东西可以卷，推导看这里

• Stirling公式

用来求\(n!\)的近似值，在\(n\)比较大的时候准确值高

\[n!\approx \sqrt{2\pi n}(\frac{n}{e})^n \]

奇偶性

\[\binom{n}{m}\%2=[n \& m=m] \]

\[{n\brace m}\%2=\binom{n-m+d-1}{d-1}\%2,d=\frac{m+1}{2} \]

一式比较简单，直接\(lucas\)定理搞一下就可以了。

\[\begin{aligned} \binom{n}{m}\%2=\binom{n\%2}{m\%2}\binom{n/2}{m/2} \end{aligned} \]

一位一位向上讨论就行了，所有的位必须是\(n_i\ge m_i\)

斯特林数就麻烦一点了，这里的思路是sdchr大佬的

首先由斯特林数的通项，我们构造一个和\(Ta\)奇偶性一样的数列

\[p_{i,j}=\left\{\begin{array} up_{i-1,j-1},m \%2=0\\ p_{i-1,j-1},p_{i-1,j},m\%2\not=0\end{array}\right. \]

然后数形结合

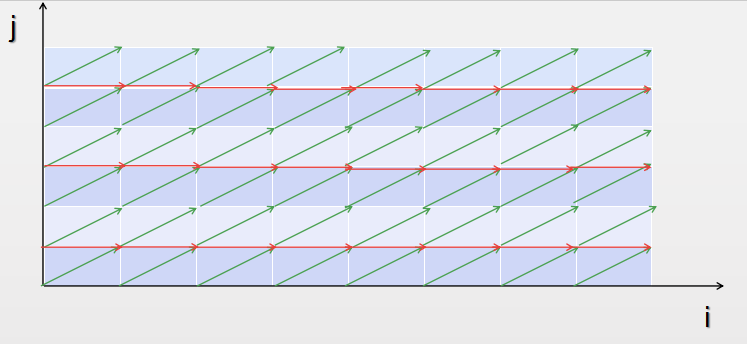
在对应位置连边后我们发现\(p_{n,m}\)就是从\((0,0)\)走到\((n,m)\)的方案数。

发现绿边一定会走\(m\)次，红边一定会走\(n-m\)次，于是统计一下红边的方案数。

发现一共有\(d=\lfloor\frac{m+1}{2}\rfloor\)次机会走红边（奇数行可以走），每次可以走任意长度

于是转换成了把\(n-m\)分成\(d\)段的方案数，插一下板就搞定了，方案数为\(\binom{n-m+d-1}{d-1}\)

拉格朗日差值法

现在有\(n\)个点\(x_i,y_i\)，可以唯一的确定一个多项式。

\[\ell_i(k)=\prod_{j=1,i\not=j}^n\frac{k-x_j}{x_i-x_j} \]

则原多项式为

\[f(k)=\sum_{i=1}^n\ell_i(k)y_i \]

化简就是系数表示法了，不过一般还是用来求点值，复杂度\(O(n^2)\)

自然数幂级数之和

\[T_k(n)=\sum_{i=0}^ni^k \]

方法1 拉格朗日差值

可以预处理\((x_1,T_k(x_1)),(x_2,T_k(x_2)),\dots,(x_k,T_k(x_k))\)这\(k\)个点，然后进行差值。

注意到

\[\ell_i(n)=\prod_{j=1,i\not=j}^k \frac{n-x_j}{x_i-x_j} \]

分母上面对同一个\(n\)可以预处理前缀积和后缀积，下面的连续的乘法，左右都是\(1\times2 \times \dots\)，因为选择的\(x\)的值在整数上连续，于是复杂度是\(O(k)\)的。

方法2 Stirling展开

\[\begin{aligned} T_k(n)&=\sum_{i=0}^ni^k\\ &=\sum_{i=0}^n\sum_{j=0}^k{k \brace j}\binom{i}{j}j!\\ &=\sum_{j=0}^k{k \brace j}j!\sum_{i=0}^n\binom{i}{j}\\ &=\sum_{j=0}^k{k \brace j}j!\binom{n+1}{j+1} \end{aligned} \]

预处理一下也是\(O(k)\)的了，\(n\)比较大的话组合数用计算式算。

提一下这个组合恒等式

\[\sum_{i=0}^n\binom{i}{j}=\binom{n+1}{j+1} \]

其实就是\(Pascal\)三角形的一列和，把这一列放到右边去加加减减就可以了。

具体点说，把计算式变一下

\[\binom{n}{j}=\binom{n+1}{j+1}-\binom{n+1}{j} \]

然后都带进去

\[\begin{aligned} \sum_{i=0}^n\binom{i}{j}&=\binom{n+1}{j+1}-\binom{n+1}{j}+\binom{n+1}{j}-\binom{n+1}{j-1}+\dots\\ &=\binom{n+1}{j+1} \end{aligned} \]

减到最后发现是\(0\)

子集和

其实是快速莫比乌斯变换(FMT)及其反演的一个小trick吧。

考虑定义一个

\[\hat{f_S}=\sum_{T \subseteq S}f_T \]

然后对一个\(|U|=n\)的全集来说，求出所有子集的这个东西的复杂度暴力枚举子集是\(O(3^n)\)的，然后有一种\(O(2^nn)\)的优秀做法。

定义

\[\hat{f_S}^{(i)}=\sum_{T\subseteq S}[(S-T)\subseteq\{1,2,\dots,i\}]f_T \]

然后考虑递推，显然有\(\hat{f_S}^{(0)}=f_S,\hat{f_S}^{(n)}=\hat{f_S}\)，分别是递推初始值和递推目标。

若\(S\bigcup\{i\}=\varnothing\)，则有

\[\hat{f}_{S\bigcup\{i\}}^{(i)}=\hat{f_S}^{(i-1)}+\hat{f}_{S\bigcup \{i\}}^{(i-1)} \]

写成代码非常简单

for(int i=1;i<1<<n;i<<=1)
    for(int s=0;s<1<<n;s++)
        if(s&i)
           f[s^i]+=f[s];

泰勒公式

• 用多项式函数去逼近光滑函数

\[f(x)=\sum_{i=0}^\infty\frac{f^{(i)}(x_0)}{i!}(x-x_0)^i \]

后缀数组

• \(LCP(i,j)=\min(LCP(i,k),LCP(k,j)),\forall 1\le i\le k\le j\le n\)，这个下标是针对字典序的。
• \(h(i)\ge h(i-1)-1\)，这个是针对原位置的。

偷了一份快读的板子

namespace io
{
	const int SIZE=(1<<21)+1;
	char ibuf[SIZE],*iS,*iT,obuf[SIZE],*oS=obuf,*oT=oS+SIZE-1,c,qu[55];
    int f,qr;
	// getchar
	#define gc() (iS==iT?(iT=(iS=ibuf)+fread(ibuf,1,SIZE,stdin),(iS==iT?EOF:*iS++)):*iS++)
	// print the remaining part
	inline void flush(){fwrite(obuf,1,oS-obuf,stdout);oS=obuf;}
	// putchar
	inline void putc(char x){*oS++=x;if(oS==oT)flush();}
	// input a signed integer
	template <class I>
	inline void read(I &x)
	{
		for(f=1,c=gc();c<'0'||c>'9';c=gc()) if(c=='-') f=-1;
		for(x=0;c<='9'&&c>='0';c=gc()) x=x*10+(c&15);x*=f;
    }
	// print a signed integer
	template <class I>
	inline void print(I &x)
	{
		if(!x)putc('0');if(x<0) putc('-'),x=-x;
		while(x)qu[++qr]=x%10+'0',x/=10;
		while(qr)putc(qu[qr--]);
	}
	//no need to call flush at the end manually
	struct Flusher_ {~Flusher_(){flush();}}io_flusher_;
}
using io::read;
using io::putc;
using io::print;

支配树

• 不会证明

• 对于一个源点为\(r\)的有向图的点\(w\)，若\(d\)点满足删去\(d\)点后\(r\)无法到达\(w\)，称作\(d\)支配\(w\)，\(d\)是\(w\)的支配点。

• 在支配\(w\)的点中，如果一个支配点满足\(i\not=w\)被\(w\)剩下所有的支配点(除\(w\)自己)，那么这个\(i\)被称为\(w\)的最近支配点，记作\(idom(w)\)，\(idom(w)\)向\(w\)连边形成的树即为支配树。

• \(DAG\)的支配树非常好求，直接按照topo排序增量法构造即可。

• 半支配点:

  对图DFS求出dfs树中每个点的dfs序\(dfn\)

  对一个点\(w\)，存在一个点\(x\)，满足\(x\)到\(w\)有一条路径，路径上的任意一点\(y\)(除去\(x\)和\(w\))满足\(dfn(y)>dfn(w)\)，称\(x\)为\(w\)的半支配点，记作\(semi(x)\)

  删掉非树边，连边\((semi(w),w)\)，不改变支配关系。

• 求半支配点

  对点\(w\)，遍历反边\((x,w)\)对应的\(x\)

  • 若\(dfn(x)<dfn(w)\)且\(dfn(x)<dfn(semi(w))\)，\(semi(w)=x\)
  • 若\(dfn(x)>dfn(w)\)，取所有满足\(dfn(y)>dfn(w)\)且\(y\)是\(x\)的祖先点\(y\)，用\(semi(y)\)尝试更新\(semi(w)\)

• 求支配点

  对于一个点\(w\)，找到路径\(w\)到\(semi(w)\)路径(不包括\(semi(w)\))上\(dfn(semi(x))\)最小的一个点\(x\)

  • 如果\(semi(x)=semi(w)\)，则\(idom(w)=semi(w)\)
  • 否则\(idom(w)=idom(x)\)

• 实现

  采用带权并查集实现，具体细节还是有一点的Code

二分图

• 最小路径覆盖

  给定有向图\(G=(V,E)\)，设\(P\)是\(G\)的一个简单路(不相交)的集合。如果\(V\)中所有顶点恰好在\(P\)的一条路上，称\(P\)是\(G\)的一个路径覆盖。

  把\(V\)中每个点拆成两个，设二分图最大匹配为\(C\)，那么\(|P|_{\min}=|G|-|C|\)，即最小路径覆盖=顶点数-最大匹配数。

  感性理解：

  显然 路径的个数+每个路径中边的数量=总点数，总点数不变，于是最大化边的数量，在拆点后的二分图中形成一个匹配等价于连上了一条有向边，于是就可以了。

• 二分图最小点覆盖

  对二分图\(G\)，求一个最小点集\(S\)，使得图中任意一条边都有至少一个端点属于\(S\)。

  \(K\ddot onig\)定理：二分图最小点覆盖的点数等于二分图最大匹配包含的边数

  构造：

  1. 求出最大匹配
  2. 从左边每个非匹配点找增广路，标记访问节点。
  3. 取左边未标记点，右边标记点

• 二分图最大独立集

  对二分图\(G\)，求一个最大点集\(S\)，使得点集任意两点都没有边相连。

  • 无向图的最大团等于其补集的最大独立集
  • 二分图\(G\)最大独立集的大小等于\(|G|-\)最小点覆盖大小

最大权闭合子图

• 闭合图

  定义一个有向图\(G=(V,E)\)的闭合图是该有向图的一个点集，且该点集的所有出边都还指向该点集。

• 最大权闭合子图

  给每个点\(v\)一个点权\(w\)，最大权闭合子图是点权和最大的一个闭合图。

• 求最大权闭合子图

  构造图\(G'=(V',E')\)，方法如下

  \(V'=V\cup\{s,t\}\)

  \(E'=E\cup\{(s,v)|v\in V,w_v>0\}\bigcup\{(v,t)|v\in V,w_v<0\}\)

  然后网络流图的容量为

  \(c(u,v)=\infty,(u,v)\in E,c(s,v)=w_v,w_v>0,c(v,t)=-w_v,w_v<0\)

  这里直接抄了论文的

  然后画了图可以形象理解理解

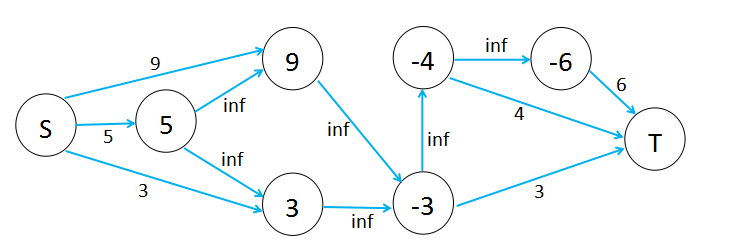
求出图\(G'\)的最小割后的\(S\)集即为\(G\)的最大权闭合子图

• 假证明

  设\(S\)图的点权和为\(C=C_1+C_2\)，其中正点权为\(C_1\),负点权为\(C_2\)。设割集的边权和为\(W=W_1+W_2\)，正边权（与\(S\)相连的被割掉的边）和为\(W_1\)，负边权和为\(W_2\)。注意：\(C_2\)在数值上是负的，\(W_2\)是正的。

  负点割给\(S\)要断掉与\(T\)相连的边，所以\(C_2+W_2=0\)，有\(C+W=C_1+W_1\)，因为右边为正点权和是定值，所以最小割最小化\(W\)就把\(C\)最大化了。

上下界网络流

• 无源汇可行流

  • 要求流量守恒
  • 要求流量满足上下界

  建图方法

  1. 对\(E(u,v,l,r)\)，建\(E'(u,v,r-l)\)

  2. 对每个点定义\(d_i=\sum f(u,i)-\sum f(i,v)\)，即流入减去流出。

     然后对\(d_i>0\)，建\(E'(ss,i,d_i)\)

     \(d_i<0\)，建\(E'(i,tt,-d_i)\)

     \(ss,tt\)是新建的超级源点与超级汇点

  感性理解

  ​ 对每个点先把下界给流了，然后不平衡的通过超级源or汇点强行补。于是最后判断是否有可行流就是看是否这些边流满了。

错位排列

额今天看了13年的容斥的那篇论文，才明白自己之前学的容斥没有一点技巧性可言，也终于明白了大家说的一下沙茶容斥是怎么一回事情

先说说容斥吧

可以用来求并集

\[\bigcup_{i=1}^n S_i=\sum_i S_i-\sum_{i<j}S_i\cap S_j+\sum_{i<j<k}S_i\cap S_j\cap S_k-\dots+(-1)^{n+1}S_1\cap S_2\cap \dots \cap S_n \]

可以用来求交集

\[\bigcap_{i=1}^nS_i=U-\bigcup_{i=1}^n\overline {S_i} \]

一般交集转化过去会比较好求

• 一般化的容斥原理，若

\[g(T)=\sum_{S\subseteq T}f(S) \]

则

\[f(T)=\sum_{S\subseteq T}(-1)^{|T|-|S|}g(S) \]

对于\(\supseteq\)也成立

• 统计一个满足\(p_i\not=i\)的长度为\(n\)的排列的数量。

  \(S_i\)代表\(p_i\not=i\)这个条件

  然后答案就是

  \[\begin{aligned} \bigcap_{i=1}^n S_i&=n!-\sum_{i=1}^n(-1)^{i-1}(n-i)!\binom{n}{i}\\ &=n!\sum_{i=0}^n\frac{(-1)^i}{i!} \end{aligned} \]

• min-max容斥

姬酸姬盒小技巧

• 形如\(ax+by+c\le 0\)的式子的方向向量有\((-b,a)\)。你可以发现\(b\)的正负是决定半平面是在直线上面还是下面的。

多点LCA

orz huyufeifei

\(k\)个点LCA的最深点是dfs序相邻两点的LCA

最浅点是dfs序最远两点的LCA

NoiLinux 使用

对拍

#include <cstdio>
#include <cstdlib>
int main()
{
	for(int i=1;i<=100;i++)
	{
		system("g++ data.cpp -o data");
		system("./data");
		system("g++ Dew.cpp -o Dew");
		system("./Dew");
		system("g++ bf.cpp -o bf");
		system("./bf");
		if(system("diff -bB Dew.out bf.out"))
		{
			printf("error in %d\n",i);
			return 0;
		}
		system("sleep 1");
	}
	return 0;
}

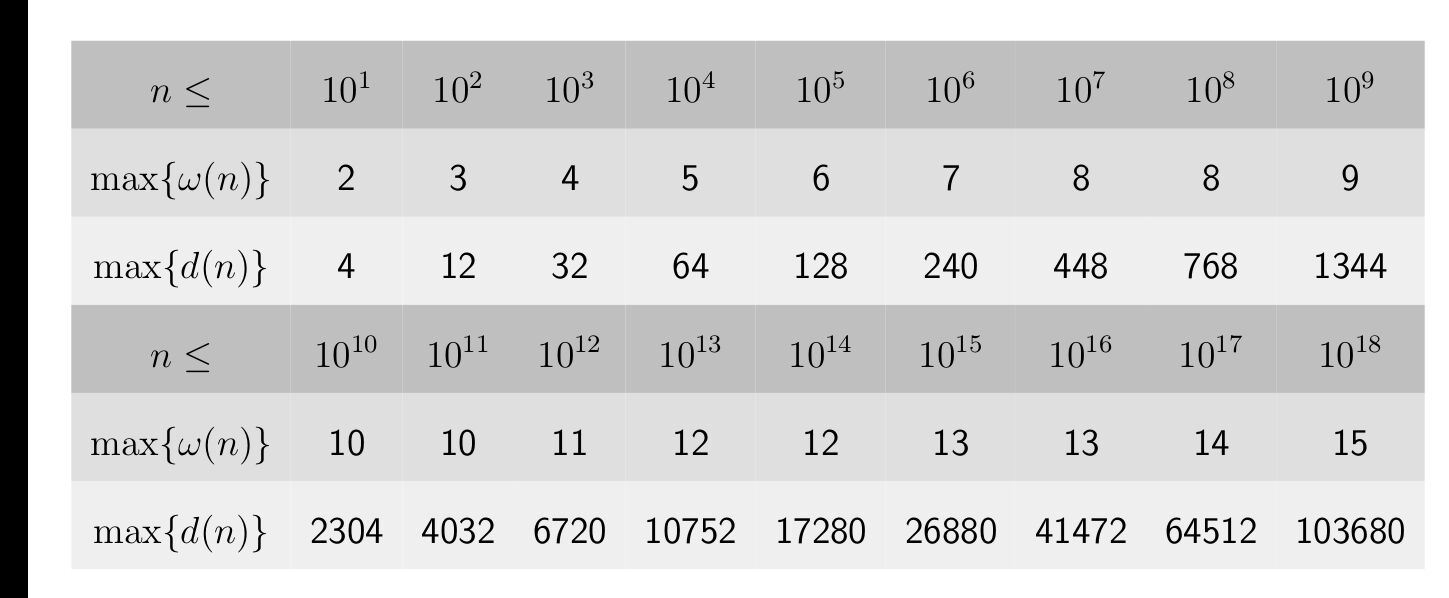
1e18内不同质因子个数和约数个数